浙教版八年级数学下册4.3 中心对称与中心对称图形--巩固练习(含答案)
文档属性
| 名称 | 浙教版八年级数学下册4.3 中心对称与中心对称图形--巩固练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 00:00:00 | ||
图片预览



文档简介
中心对称与中心对称图形--巩固练习
一. 选择题
1. (2020﹒枣阳市校级模拟)下列四个交通标志图案中,是中心对称图形的为( )
A. B. C. D.
2. (2020﹒凉山州一模)如图,AB垂直于BC且AB=BC=3cm,?OA与?OC关于点O中心对称,AB、BC、?OA、?OC所围成的图形的面积是( .
A. B. C. D.
3. (2019秋﹒溧阳市期末)在四张完全相同的卡片上.分别画有等腰三角形、矩形、菱形、圆,现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
A. B. C. D.1
4.(2020﹒谷城县校级模拟)下列图形:①线段;②角;③等边三角形;④平行四边形;⑤矩形;⑥菱形;⑦正方形,既是轴对称图形,又是中心对称图有几个( )
A.3 B.4 C.5 D.6
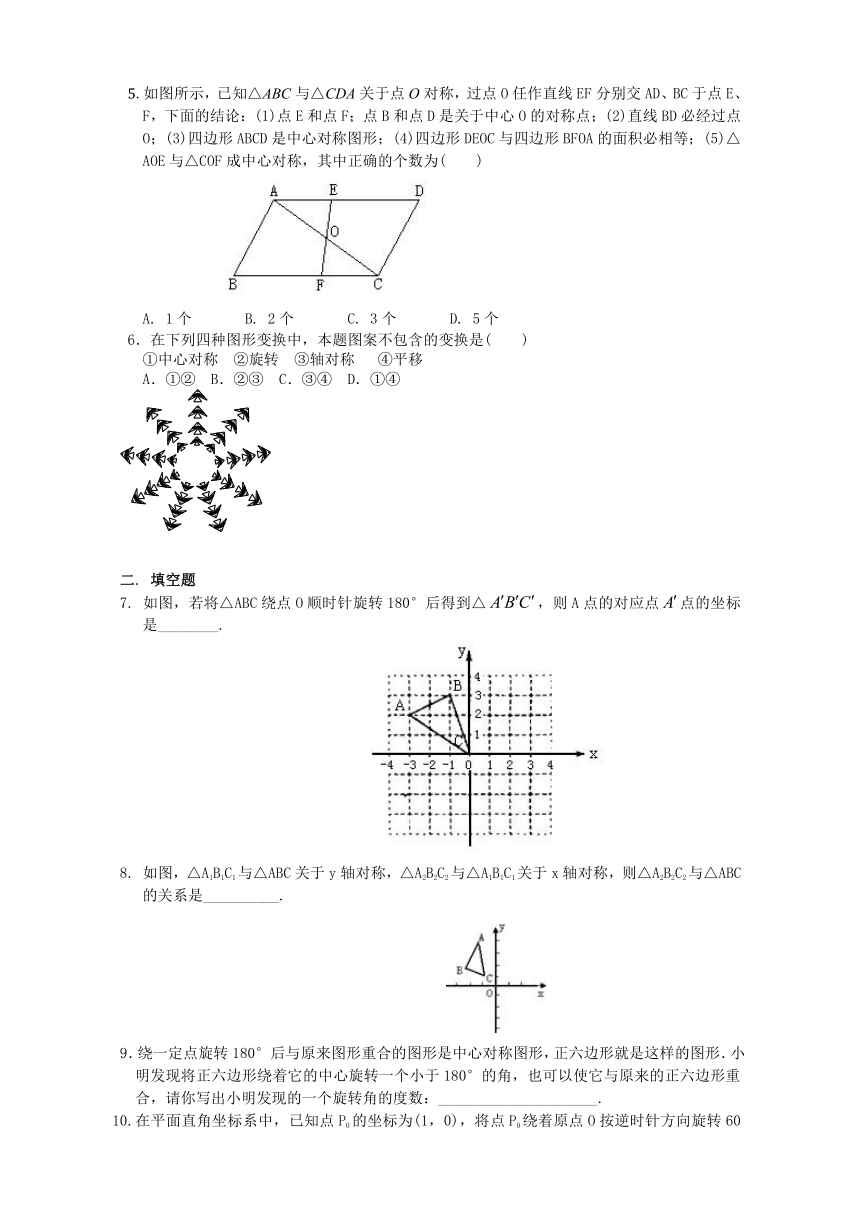
5.如图所示,已知△ABC与△CDA关于点O对称,过点O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F;点B和点D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 5个
6.在下列四种图形变换中,本题图案不包含的变换是( )
①中心对称 ②旋转 ③轴对称 ④平移
A.①② B.②③ C.③④ D.①④
二. 填空题
7. 如图,若将△ABC绕点O顺时针旋转180°后得到△,则A点的对应点点的坐标是________.
8. 如图,△A1B1C1与△ABC关于y轴对称,△A2B2C2与△A1B1C1关于x轴对称,则△A2B2C2与△ABC的关系是__________.
9.绕一定点旋转180°后与原来图形重合的图形是中心对称图形,正六边形就是这样的图形.小明发现将正六边形绕着它的中心旋转一个小于180°的角,也可以使它与原来的正六边形重合,请你写出小明发现的一个旋转角的度数:_____________________.
10.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
11.如图所示,△ABC中,∠BAC=120°,∠DAE=60°,AB=AC,△AEC绕点A旋转到△AFB的位置;∠FAD=__________,∠FBD=__________.
12. (2016?杭州)在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D关于坐标原点的对称点的坐标为 .
三. 综合题
13. 如图,△DEF是由△ABC绕点O顺时针旋转180°后得到的图形.
(1)请指出图中所有相等的线段;
(2)写出图中所有相等的角;
(3)图中哪些三角形可以看成是关于点O成中心对称的?
14.如图,矩形ABCD在平面直角坐标系的位置如图,A(0,0)、B(6,0)、D(0,4).
(1)根据图形直接写出点C的坐标: ;
(2)已知直线m经过点P(0,6)且把矩形ABCD分成面积相等的两部分,请只用直尺准确地画出直线m,并求该直线m的解析式.
15. 如图,为边的是等边三角形,
求AP的最大、最小值.
16.(2019秋﹒沙坪坝区校级期中)在学习函数的过程中,我们经历了“确定函数的表达式--利用函数图象研究其性质--运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=中,当x=-1时,y=4;当x=-2时 y=0.
(1)根据已知条件可知这个函数的表达式 y=.
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 (0,-2)成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
17.(2019春﹒宿州期中)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称?
(2)若△ADC的面积为4,求△ABE的面积.
18.(2018秋﹒呼和浩特期中)如图,△ABC中,D是BC上一点,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E、F关于直线AD对称.
附加题:(2019春﹒景德镇期中)如图,由4个全等的正方形组成的L形图案,请按下列要求画图:
(1)在图案①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图案②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图案③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.
:
【答案与解析】
一、选择题
1.【答案】B.
2.【答案】A
3.【答案】C
4.【答案】B
5.【答案】D
【解析】已知△ABC与△CDA关于点O对称,所以点A对称点是点C, 点B对称点是点D,即四边形ABCD是平行四边形,从而推得(1)(2)(3)(4)(5)正确。
6.【答案】D
【解析】旋转180°与原图像不能重合,所以①是错误的;平移应该是整个图形通过平移得到新图形,所以④是错误的.
二、填空题
7.【答案】(3,-2)
8.【答案】关于原点O中心对称.
【解析】通过画图可以发现经过两次轴对称,在第四象限,与原三角形中心对称.
9.【答案】60°或120°.
【解析】正六边形的中心角是360°÷6=60°,所以旋转角是60°的倍数即可.
10.【答案】
【解析】准确的画图将为我们研究问题提供较好的思维切入点,据题意,画示意图.
由图可知,P3与P2关于y轴对称,因此只须求得P2坐标,而我们可 以发现△OP0P2为含60°角的直角三角形,所以可以知道 ,.
11.【答案】60°;60°.
【解析】因为△AEC绕点A旋转到△AFB的位置,所以△AEC≌△AFB,
即∠FAB=∠EAC,∠ACB=
∠FBA,又因为∠BAC=120°,∠DAE=60°,
所以∠FAD=∠BAD +∠FAB=∠BAD+∠EAC =120°-
60°=60°;所以∠FBD=∠ABC+∠FBA=∠ABC+∠ACB=180°-120°=60°.
12.【答案】(﹣5,﹣3).
【解析】如图所示:∵A(2,3),B(0,1),C(3,1),线段AC与BD互相平分,
∴D点坐标为:(5,3),
∴点D关于坐标原点的对称点的坐标为:(﹣5,﹣3).
三.解答题
13.【解析】
因为△DEF是由△ABC绕点O顺时针旋转180°后得到的,所以这两个三角形关于
点O成中心对称
(1)图中相等的线段有:
(2)图中相等的角有:
(3)图中关于点O成中心对称的三角形有:
△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
14.【解析】
解:(1)∵B(6,0)、D(0,4),
∴点C的横坐标是6,纵坐标是4,
∴点C的坐标为(6,4);
故答案为:(6,4);
(2)直线m如图所示,
对角线OC、BD的交点坐标为(3,2),
设直线m的解析式为y=kx+b(k≠0),
则,
解得,
所以,直线m的解析式为y=﹣x+6.
15.【解析】已知条件AB=3,AC=2与所求的AP比较分散.考虑到是等边三角形,
若绕点P逆时针旋转到,
则
可得是等边三角形,,
则与所求就集中到中
(特殊情况A,,B三点在同一直线).
由于,
所以.
即 AP的最大值为5,最小值为1.
16.【考点】函数的图象;中心对称;坐标与图形变化-旋转.
(3)①观察图象可知:函数图象关于(0,2)成中心对称.
故答案为(0,-2).
②观察图象可知:当-1<x<1时,y随着x的增大而减小.
③观察图象可知:若直线y=c与该图象有3个交点,c的取值范围为0<c<4.【点评】本题考查函数的性质,中心对称,坐标与图形的性质,解题的关键是理解题意,学会利用数形结合的思想解决问题,属于中考常考题型.
17. 【分析】(1)直接利用中心对称的定义写出答案即可;
(2)根据成中心对称的图形的两个图形全等确定三角形BDE的面积,根据等底同高确定ABD的面积,从而确定ABE的面积.
【解答】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8.
【点评】本题考查了中心对称的定义,解题的关键是了解中心对称的定义,难度较小.
18.【专题】多边形与平行四边形.【分析】(1)判定四边形AEDF是平行四边形,即可得出四边形AEDF是中心对称图形;
(2)先得出AE=DE,再根据四边形AEDF是平行四边形,可得四边形AEDF是菱形,即可得到结论.
【解答】解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴四边形AEDF是中心对称图形;
(2)∵AD平分∠BAC,
∴∠BAD=∠CAD,
又∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE,
又∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,
∴AD垂直平分EF,
∴点E、F关于直线AD对称.
【点评】本题考查了中心对称,平行四边形是中心对称图形,对称中心是对角线的交点.
附加题:
解:如图所示.
(1)如图(1),图(2),图(3)所示;
(2)如图(4)所示;
(3)如图(5),图(6)所示.
【点评】本题综合考查了中心对称图形及轴对称图形的性质,及其作图的方法,学生做这些题时找对称轴及对称点是关键.
PAGE
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
