浙教版八年级数学上册1.1. 2认识三角形课件(18张PPT)
文档属性
| 名称 | 浙教版八年级数学上册1.1. 2认识三角形课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 217.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 09:12:08 | ||
图片预览





文档简介
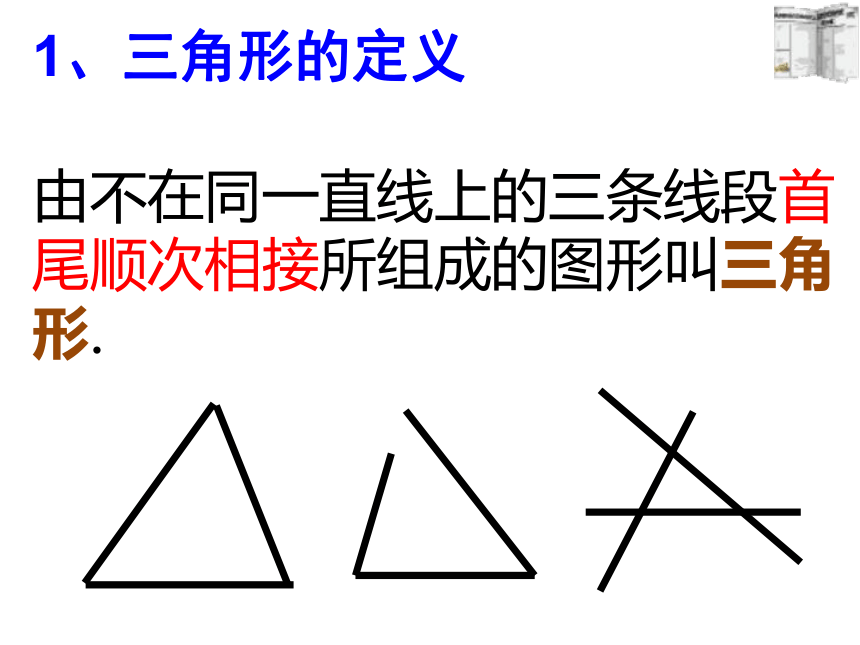
课件18张PPT。1.1 认识三角形21、三角形的定义
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形.
1.图中有几个三角形?用符号表示这些三角形和各自的边角2.以AB为边的三角形有哪些?△ABC、△ABE3.以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE练习4.以∠D为角的三角形有哪些?△ BCD、 △DEC1.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
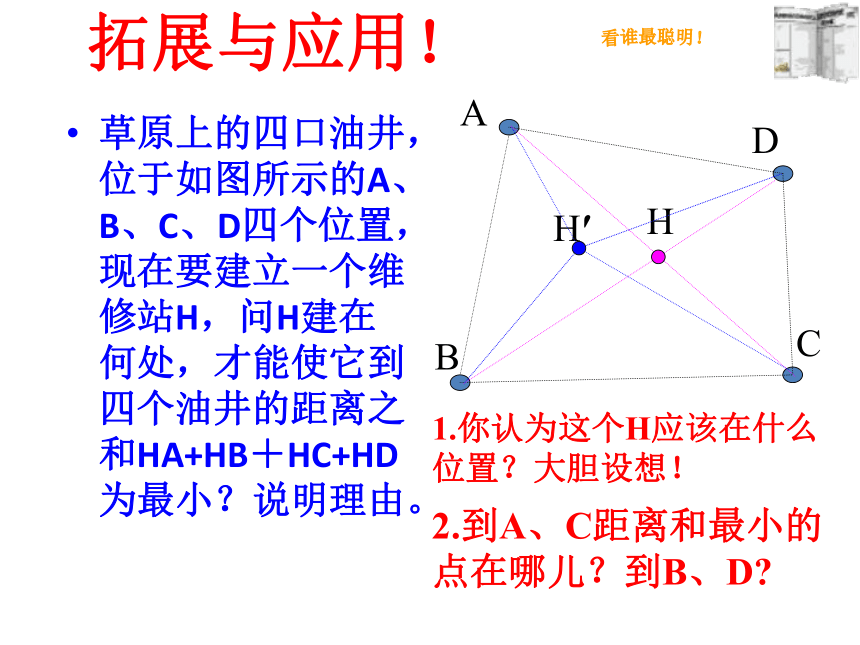
(4) 3,5,8 ( )不能能能不能练一练试一试2.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?小颖有5种选法。第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!考考你!答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多。草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。拓展与应用!ADCBHH′1.你认为这个H应该在什么位置?大胆设想!2.到A、C距离和最小的点在哪儿?到B、D?看谁最聪明!用三根木棒钉一个三角形,你会发现再也无法改变这个
三角形的形状和大小,也就是说,如果一个三角形的
三条边固定了,那么三角形的形状和大小就完全确定了.
在数学上把三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生活中有广泛的应用,你能举出哪些例子吗?三角形的角平分线 在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段,叫做三角形的角平分线.如图:线段AD叫做ΔABC的角平分线。画出ΔABC的另外两条角平分线;
观察三条角平分线,说说你的发现。对于其它的任意三角形是不是也有同样的结果?三角形的三条角平分线在三角形的内部交于一点∵BE是△ABC的角平分线∴____ =_____= _____∴∠ACB=2______=2______∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF 三角形的中线 在三角形中,连结三角形的一个顶点与该顶点对边中点的线段,叫做这个三角形的中线.如图:线段AD叫做ΔABC的边BC上的中线。(1)画出ΔABC的另外两边上的中线;(2)说出哪条线段是ΔABC的哪条边上的中线;把刚才的锐角三角形换成直角三角形或钝角三角形,结果又怎么样呢?三角形的三条中线在三角形的内部交于一点∵AD是△ ABC的中线三角形三条中线的交点叫做三角形的重心;三角形的高从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线.如图, 线段AD是BC边上的高.注意标明垂直的记号和垂足的字母.
∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°例1: 在△ ABC中,AD、AE分别是它的角平分线和高,且∠ B = 35°, ∠ C = 65°,
求∠ DAE的度数例2:如图:在△ ABC中,AD是BC边上的高线,CE是一条角平分线,它们相交于点P,已知∠ APE=55°, ∠ AEP=80°。求△ ABC的各个内角的度数。通过本节课的学习,你有哪些收获?三角形的角平分线、中线和高线.
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形.
1.图中有几个三角形?用符号表示这些三角形和各自的边角2.以AB为边的三角形有哪些?△ABC、△ABE3.以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE练习4.以∠D为角的三角形有哪些?△ BCD、 △DEC1.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )不能能能不能练一练试一试2.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?小颖有5种选法。第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!考考你!答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多。草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。拓展与应用!ADCBHH′1.你认为这个H应该在什么位置?大胆设想!2.到A、C距离和最小的点在哪儿?到B、D?看谁最聪明!用三根木棒钉一个三角形,你会发现再也无法改变这个
三角形的形状和大小,也就是说,如果一个三角形的
三条边固定了,那么三角形的形状和大小就完全确定了.
在数学上把三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生活中有广泛的应用,你能举出哪些例子吗?三角形的角平分线 在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段,叫做三角形的角平分线.如图:线段AD叫做ΔABC的角平分线。画出ΔABC的另外两条角平分线;
观察三条角平分线,说说你的发现。对于其它的任意三角形是不是也有同样的结果?三角形的三条角平分线在三角形的内部交于一点∵BE是△ABC的角平分线∴____ =_____= _____∴∠ACB=2______=2______∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF 三角形的中线 在三角形中,连结三角形的一个顶点与该顶点对边中点的线段,叫做这个三角形的中线.如图:线段AD叫做ΔABC的边BC上的中线。(1)画出ΔABC的另外两边上的中线;(2)说出哪条线段是ΔABC的哪条边上的中线;把刚才的锐角三角形换成直角三角形或钝角三角形,结果又怎么样呢?三角形的三条中线在三角形的内部交于一点∵AD是△ ABC的中线三角形三条中线的交点叫做三角形的重心;三角形的高从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线.如图, 线段AD是BC边上的高.注意标明垂直的记号和垂足的字母.
∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°例1: 在△ ABC中,AD、AE分别是它的角平分线和高,且∠ B = 35°, ∠ C = 65°,
求∠ DAE的度数例2:如图:在△ ABC中,AD是BC边上的高线,CE是一条角平分线,它们相交于点P,已知∠ APE=55°, ∠ AEP=80°。求△ ABC的各个内角的度数。通过本节课的学习,你有哪些收获?三角形的角平分线、中线和高线.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
