浙教版八年级数学下册第四章平行四边形的综合题复习培优讲义(走进重高 含答案)
文档属性
| 名称 | 浙教版八年级数学下册第四章平行四边形的综合题复习培优讲义(走进重高 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 666.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 00:00:00 | ||
图片预览




文档简介
平行四边形的综合复习培优讲义(走进重高)
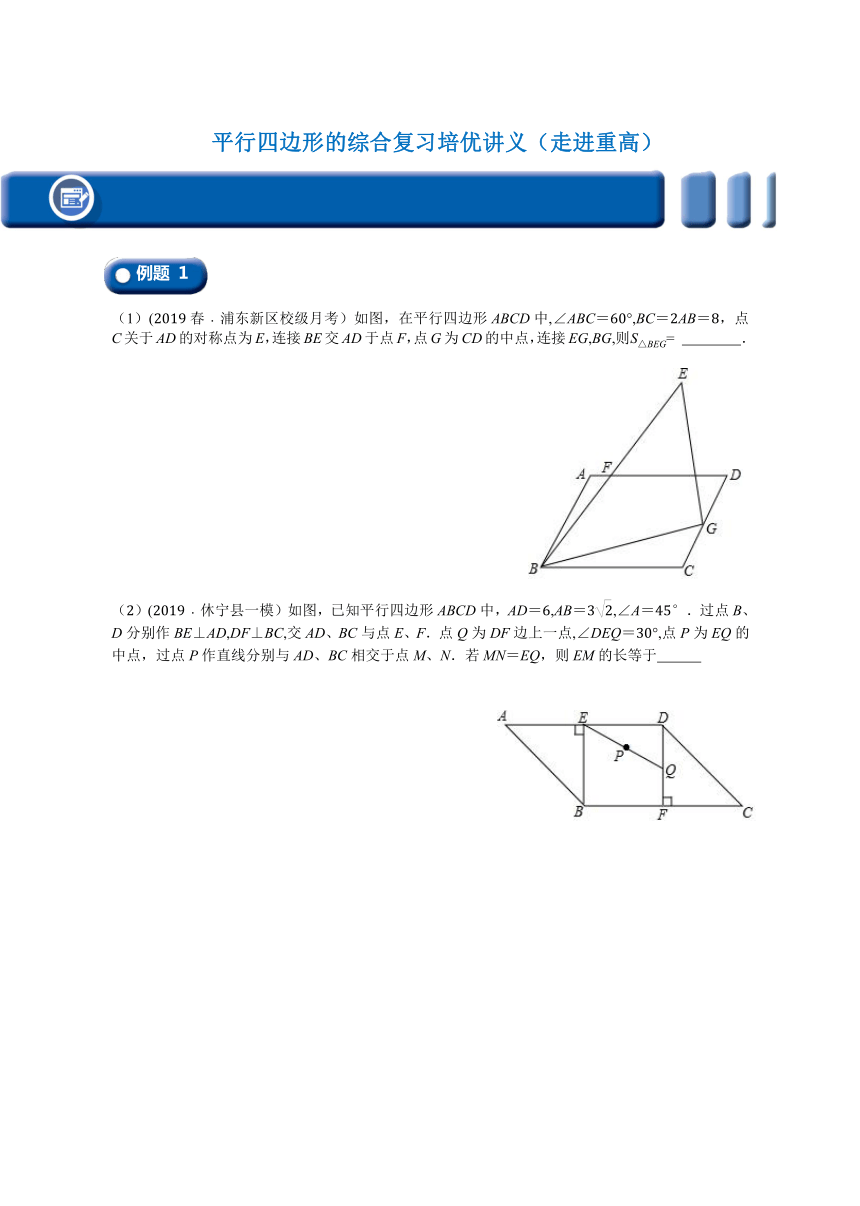
(1)(2019春﹒浦东新区校级月考)如图,在平行四边形ABCD中,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG,BG,则= .
(2)(2019﹒休宁县一模)如图,已知平行四边形ABCD中,AD=6,AB==45°.过点B、D分别作BE⊥AD,DF⊥BC,交AD、BC与点E、F.点Q为DF边上一点,∠DEQ=30°,点P为EQ的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=EQ,则EM的长等于
(3)如图1-3,在中,,,于E,则________.
(4)如图1-4,与的周长相等,且,,则的度数为________.
图1-3 图1-4
(1)14
(2)1或2;
(3)∵四边形ABCD是平行四边形,∴,又∵
∴,又∵,
∴
(4)∵与的周长相等,且,
∴,
∴,
∵,,
∴,,
∴,
∴.
(1)如图,中,P是四边形内任意一点,,,,的面积分别为,,,,则一定成立的是( )
A. B.
C. D.
(2)如图,中,平行于边的两条线段EF,GH把分成四部分,分别记这四部分的面积为,,和,则下列等式一定成立的是( ).
A. B.
C. D.
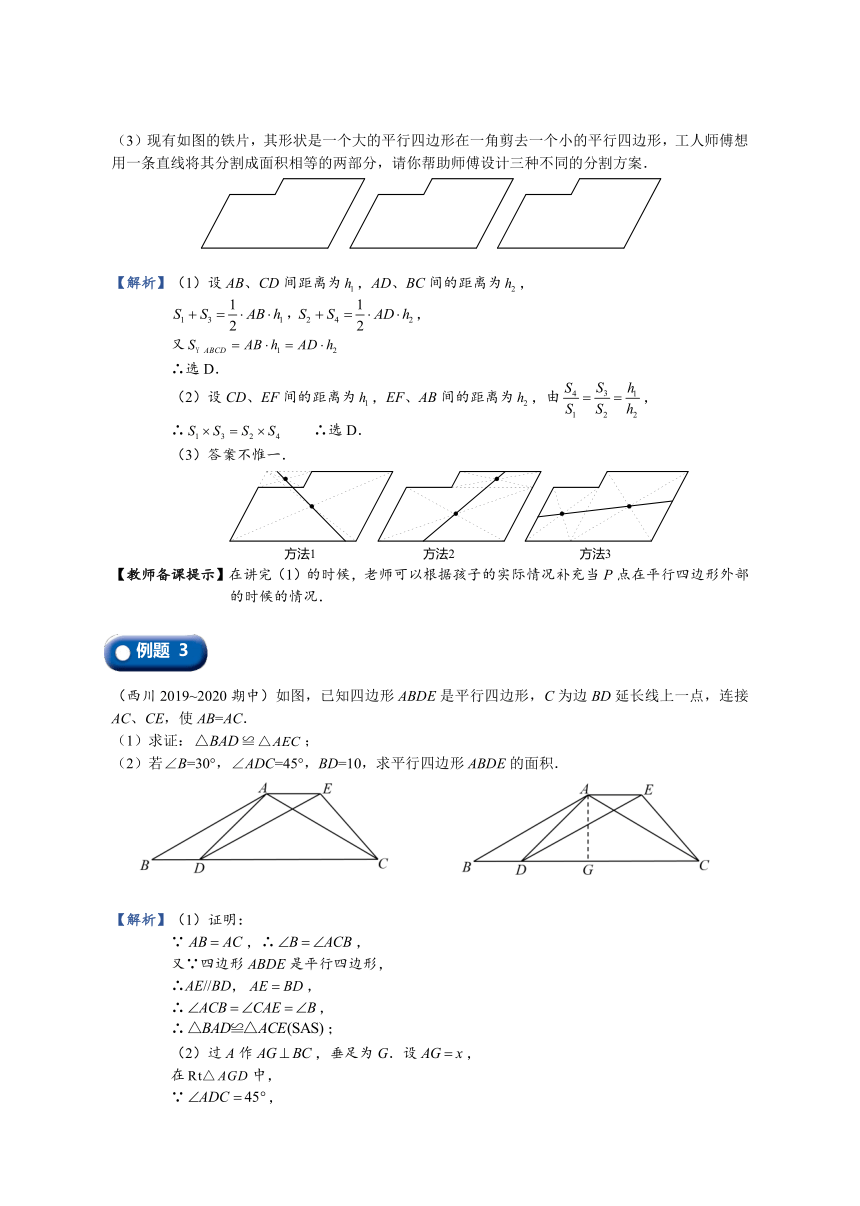
(3)现有如图的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮助师傅设计三种不同的分割方案.
(1)设AB、CD间距离为,AD、BC间的距离为,
,
又
∴选D.
(2)设CD、EF间的距离为,EF、AB间的距离为,由,
∴ ∴选D.
(3)答案不惟一.
【教师备课提示】在讲完(1)的时候,老师可以根据孩子的实际情况补充当P点在平行四边形外部的时候的情况.
(西川2019~2020期中)如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连接AC、CE,使AB=AC.
(1)求证:≌;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
(1)证明:
∵,∴,
又∵四边形ABDE是平行四边形,
∴AE//BD,,
∴,
∴;
(2)过A作,垂足为G.设,
在中,
∵,
∴,
在中,
∵,
∴,
又∵.
∴,
即,,
解得,
∴S平行四边形ABDE =BDAG=10×()=.
【教师备课提示】学校主要会把平行四边形的性质结合面积的计算来考查,所以通过这题让孩子们理解通过作高求平行四边形面积.
已知在中,于E,DF平分交线段AE于F.
(1)如图4-1,若,,请直接写出线段CD与之间所满足的关系;
(2)如图4-2,若,你在(1)中得到的结论是否仍然成立,若成立,对你的结论加以证明. 若不成立,请说明理由.
图4-1 图4-2
(1).
(2)(1)中的结论仍然成立.
证明:延长EA到G,使得,连接DG.
∵四边形ABCD是平行四边形,
∴,AB//CD,.
∵于点E,
∴.
∴.
∴.
∵,
∴.
∴,.
∴.
∵DF平分,
∴.
∵,,又
∴,
∴.
∴.
∴.
∴.
即.
【教师备课提示】这道题是平行四边形和全等综合,主要是通过平行四边形来复习孩子们对于全等的感觉,也慢慢培养孩子的综合能力.
对于下列说法,正确的请给出证明,错误的请举出反例.
(1)一组对边平行,一组对角相等的四边形是平行四边形.
(2)一组对边平行,另一组对边相等的四边形是平行四边形.
(3)一组对角相等,一条对角线平分另一条对角线的四边形是平行四边形.
(4)一组对边相等,一条对角线平分另一条对角线的四边形是平行四边形.
(5)一组对边相等,一组对角相等的四边形是平行四边形.
(1)正确.如图1所示,设AB//CD,,此时与互补,和互补,从而,故四边形ABCD是平行四边形.
(2)错误.如图2所示,在四边形ABCD中,,,但四边形ABCD不是平行四边形.
(3)错误.如图3所示,,,但四边形ABCD不是平行四边形.
(4)错误.如图4所示,在四边形ABCD中,,,但四边形ABCD不是平行四边形.(构造办法:作平行四边形,在上取点B或延长至点B,使,连接AB即得).
(5)错误.如图5所示,作等腰三角形ABE,在底边BE上取一点C(C不是BE的中点),作关于AC的垂直平分线l对称的,则在四边形ABCD中,,,但四边形ABCD不是平行四边形(∵,,∴)
图1 图2 图3
图4 图5
已知四边形ABCD,从下列条件中:①AD//BC;②AB//CD;③;④;⑤;⑥;任取其中两个,可以得出“四边形ABCD是平行四边形ABCD”这一结论的情况有
( ).
A.4种 B.9种 C.13种 D.15种
B.
【教师备课提示】通过这道题加深孩子们对于平行四边形判定条件的理解.
在中,E、F在BD上,且,点G、H分别在AD、BC上,且,GH与BD交于点O,求证:EG//HF,.
连接GF、EH,
∵四边形ABCD为平行四边形,
∴AD//BC,,
∴,,
∵,∴,
∴,
∴,,
∵,∴,
∴四边形EHFG为平行四边形,
∴EG//HF,.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若,且.求证:四边形ABCD是平行四边形.
延长PA、PC,使、.
连接MF、EN、ME、NF.
∵,∴
∴四边形MFNE是平行四边形.
∴,
∵,
∴,∴
∴,,
∴,∴
∴四边形ABCD是平行四边形.
1.在中,若周长为54cm,,则_______cm.
2.在平行四边形ABCD中,,则等于( ).
A. B. C. D.
3.在平行四边形ABCD中,点、、、和、、、分别为AB和CD的五等分点,点、和、分别是BC和DA的三等分点,已知四边形的面积1,则平行四边形ABCD面积为( ).
A.2 B. C. D.15
1.16;2.C;3.C.
4.(西川期中改编)如图,在中,,F是AD的中点,作,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是________.(把所有正确结论的序号都填在横线上)
①;②;③;④.
①②④;提示:延长EF,CD交于点G即可.
【教师备课提示】这道题是一道考试B填的改编题,比较综合,主要考察平行四边形和全等的综合,老师可以根据时间决定评讲的详略.
5.在中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.已知,,;则__________,=__________.
(1)证明:
∵在平行四边形ABCD中,E是AD边上的中点,
∴,,
∴,
∴;
(2)过B点作交DA的延长线于G点
∵
∴
∴,
又,则
∴
∴
∴.
6.如图,过平行四边形ABCD对角线的交点O作直线EF交AD、BC分别于E、F,又G、H分别为OD、OB的中点,求证:四边形EHFG为平行四边形.
易证,,
∴四边形EHFG为平行四边形.
7.如图,在平行四边形ABCD中,,,.求证:EF与MN互相平分.
连接MF、FN、EN、ME,
∵,,
∴AE//CF,
∵ABCD是平行四边形,
∴AD//BC,
∴AECF是平行四边形,从而.
∴,.
又由已知,
所以,①
又因为,,,
所以,
所以②,
由①②得四边形ENFM是平行四边形,故对角线EF与MN互相平分.
(1)(2019春﹒浦东新区校级月考)如图,在平行四边形ABCD中,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG,BG,则= .
(2)(2019﹒休宁县一模)如图,已知平行四边形ABCD中,AD=6,AB==45°.过点B、D分别作BE⊥AD,DF⊥BC,交AD、BC与点E、F.点Q为DF边上一点,∠DEQ=30°,点P为EQ的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=EQ,则EM的长等于
(3)如图1-3,在中,,,于E,则________.
(4)如图1-4,与的周长相等,且,,则的度数为________.
图1-3 图1-4
(1)14
(2)1或2;
(3)∵四边形ABCD是平行四边形,∴,又∵
∴,又∵,
∴
(4)∵与的周长相等,且,
∴,
∴,
∵,,
∴,,
∴,
∴.
(1)如图,中,P是四边形内任意一点,,,,的面积分别为,,,,则一定成立的是( )
A. B.
C. D.
(2)如图,中,平行于边的两条线段EF,GH把分成四部分,分别记这四部分的面积为,,和,则下列等式一定成立的是( ).
A. B.
C. D.
(3)现有如图的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮助师傅设计三种不同的分割方案.
(1)设AB、CD间距离为,AD、BC间的距离为,
,
又
∴选D.
(2)设CD、EF间的距离为,EF、AB间的距离为,由,
∴ ∴选D.
(3)答案不惟一.
【教师备课提示】在讲完(1)的时候,老师可以根据孩子的实际情况补充当P点在平行四边形外部的时候的情况.
(西川2019~2020期中)如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连接AC、CE,使AB=AC.
(1)求证:≌;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
(1)证明:
∵,∴,
又∵四边形ABDE是平行四边形,
∴AE//BD,,
∴,
∴;
(2)过A作,垂足为G.设,
在中,
∵,
∴,
在中,
∵,
∴,
又∵.
∴,
即,,
解得,
∴S平行四边形ABDE =BDAG=10×()=.
【教师备课提示】学校主要会把平行四边形的性质结合面积的计算来考查,所以通过这题让孩子们理解通过作高求平行四边形面积.
已知在中,于E,DF平分交线段AE于F.
(1)如图4-1,若,,请直接写出线段CD与之间所满足的关系;
(2)如图4-2,若,你在(1)中得到的结论是否仍然成立,若成立,对你的结论加以证明. 若不成立,请说明理由.
图4-1 图4-2
(1).
(2)(1)中的结论仍然成立.
证明:延长EA到G,使得,连接DG.
∵四边形ABCD是平行四边形,
∴,AB//CD,.
∵于点E,
∴.
∴.
∴.
∵,
∴.
∴,.
∴.
∵DF平分,
∴.
∵,,又
∴,
∴.
∴.
∴.
∴.
即.
【教师备课提示】这道题是平行四边形和全等综合,主要是通过平行四边形来复习孩子们对于全等的感觉,也慢慢培养孩子的综合能力.
对于下列说法,正确的请给出证明,错误的请举出反例.
(1)一组对边平行,一组对角相等的四边形是平行四边形.
(2)一组对边平行,另一组对边相等的四边形是平行四边形.
(3)一组对角相等,一条对角线平分另一条对角线的四边形是平行四边形.
(4)一组对边相等,一条对角线平分另一条对角线的四边形是平行四边形.
(5)一组对边相等,一组对角相等的四边形是平行四边形.
(1)正确.如图1所示,设AB//CD,,此时与互补,和互补,从而,故四边形ABCD是平行四边形.
(2)错误.如图2所示,在四边形ABCD中,,,但四边形ABCD不是平行四边形.
(3)错误.如图3所示,,,但四边形ABCD不是平行四边形.
(4)错误.如图4所示,在四边形ABCD中,,,但四边形ABCD不是平行四边形.(构造办法:作平行四边形,在上取点B或延长至点B,使,连接AB即得).
(5)错误.如图5所示,作等腰三角形ABE,在底边BE上取一点C(C不是BE的中点),作关于AC的垂直平分线l对称的,则在四边形ABCD中,,,但四边形ABCD不是平行四边形(∵,,∴)
图1 图2 图3
图4 图5
已知四边形ABCD,从下列条件中:①AD//BC;②AB//CD;③;④;⑤;⑥;任取其中两个,可以得出“四边形ABCD是平行四边形ABCD”这一结论的情况有
( ).
A.4种 B.9种 C.13种 D.15种
B.
【教师备课提示】通过这道题加深孩子们对于平行四边形判定条件的理解.
在中,E、F在BD上,且,点G、H分别在AD、BC上,且,GH与BD交于点O,求证:EG//HF,.
连接GF、EH,
∵四边形ABCD为平行四边形,
∴AD//BC,,
∴,,
∵,∴,
∴,
∴,,
∵,∴,
∴四边形EHFG为平行四边形,
∴EG//HF,.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若,且.求证:四边形ABCD是平行四边形.
延长PA、PC,使、.
连接MF、EN、ME、NF.
∵,∴
∴四边形MFNE是平行四边形.
∴,
∵,
∴,∴
∴,,
∴,∴
∴四边形ABCD是平行四边形.
1.在中,若周长为54cm,,则_______cm.
2.在平行四边形ABCD中,,则等于( ).
A. B. C. D.
3.在平行四边形ABCD中,点、、、和、、、分别为AB和CD的五等分点,点、和、分别是BC和DA的三等分点,已知四边形的面积1,则平行四边形ABCD面积为( ).
A.2 B. C. D.15
1.16;2.C;3.C.
4.(西川期中改编)如图,在中,,F是AD的中点,作,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是________.(把所有正确结论的序号都填在横线上)
①;②;③;④.
①②④;提示:延长EF,CD交于点G即可.
【教师备课提示】这道题是一道考试B填的改编题,比较综合,主要考察平行四边形和全等的综合,老师可以根据时间决定评讲的详略.
5.在中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.已知,,;则__________,=__________.
(1)证明:
∵在平行四边形ABCD中,E是AD边上的中点,
∴,,
∴,
∴;
(2)过B点作交DA的延长线于G点
∵
∴
∴,
又,则
∴
∴
∴.
6.如图,过平行四边形ABCD对角线的交点O作直线EF交AD、BC分别于E、F,又G、H分别为OD、OB的中点,求证:四边形EHFG为平行四边形.
易证,,
∴四边形EHFG为平行四边形.
7.如图,在平行四边形ABCD中,,,.求证:EF与MN互相平分.
连接MF、FN、EN、ME,
∵,,
∴AE//CF,
∵ABCD是平行四边形,
∴AD//BC,
∴AECF是平行四边形,从而.
∴,.
又由已知,
所以,①
又因为,,,
所以,
所以②,
由①②得四边形ENFM是平行四边形,故对角线EF与MN互相平分.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
