初中数学浙教版八年级下册4.2 平行四边形-对角线相互平分 同步训练(含解析)
文档属性
| 名称 | 初中数学浙教版八年级下册4.2 平行四边形-对角线相互平分 同步训练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览



文档简介
初中数学浙教版八年级下册4.2 平行四边形-对角线相互平分 同步训练
一、基础夯实
1.平行四边形所具有的性质是(?? )
A.?对角线相等???????????B.?邻边互相垂直???????????C.?每条对角线平分一组对角???????????D.?两组对边分别相等
2.在平行四边形 中,对角线 相交于点 ,若 ,则 的周长为(??? ) 21世纪教育网版权所有
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,在 ABCD中,AC与BD相交于点O,则下列结论不一定成立是( ??)
A.?BO=DO??????????????????????????B.?AB=CD??????????????????????????C.?∠BAD=∠BCD??????????????????????????D.?AC=BD
4.ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是(?? )
A.?10?????????????????????????????????????????B.?11?????????????????????????????????????????C.?12?????????????????????????????????????????D.?22
5.如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为16,则AC与BD的和是(??? )
A.?22?????????????????????????????????????????B.?20?????????????????????????????????????????C.?16?????????????????????????????????????????D.?10
6.如图所示,在□ABCD中,对角线AC、BD相交于点O , 且AB≠AD , 则下列式子错误的是()
A.?AC⊥BD?????????????????????????B.?AB=CD?????????????????????????C.?BO=OD?????????????????????????D.?∠BAD=∠BCD
7.如图,平行四边形ABCD的对角线AC、BD相交于点O , 若AC+BD=24厘米,△OAB的周长是18厘米,则AB的长为(?? ) 21教育网
A.?6厘米?????????????????????????????????B.?12厘米?????????????????????????????????C.?5厘米?????????????????????????????????D.?9厘米
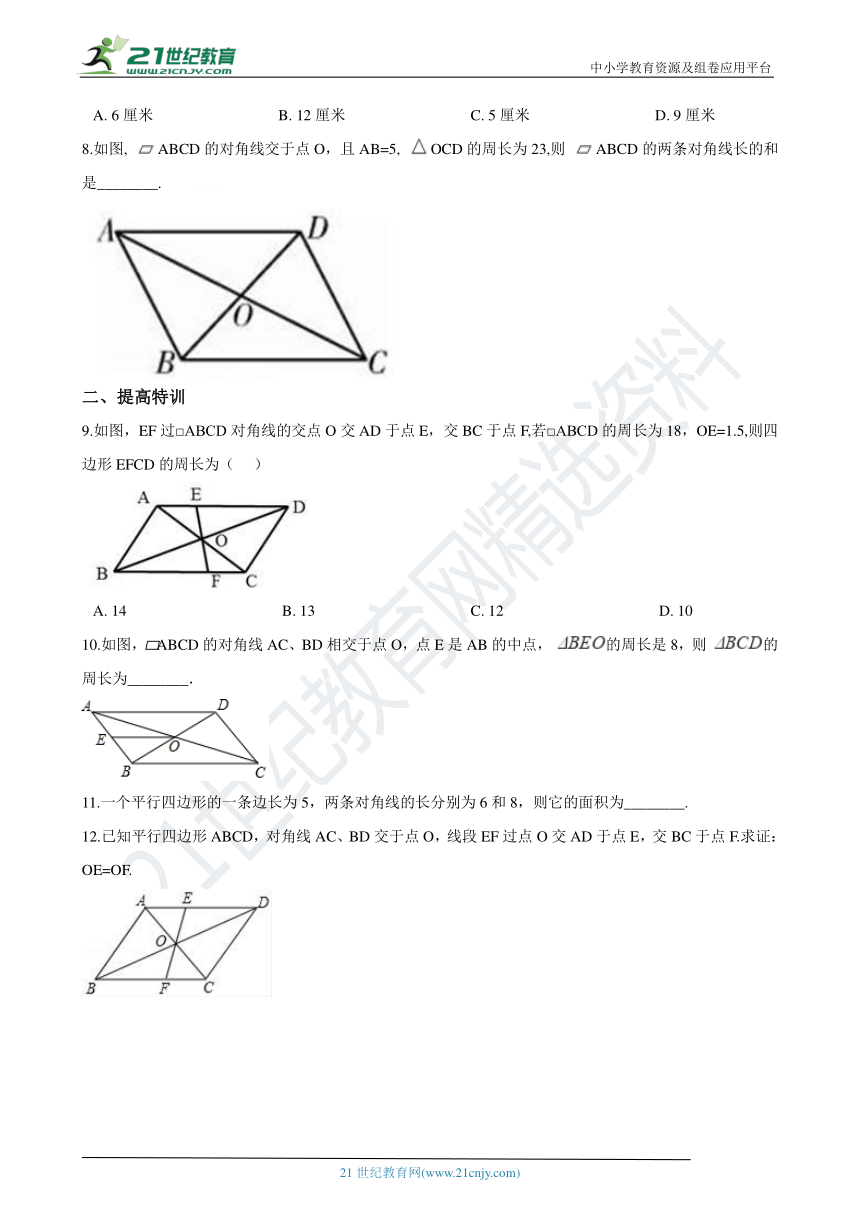
8.如图, ABCD的对角线交于点O,且AB=5, OCD的周长为23,则 ABCD的两条对角线长的和是________. 21·cn·jy·com
二、提高特训
9.如图,EF过□ABCD对角线的交点O交AD于点E,交BC于点F,若□ABCD的周长为18,OE=1.5,则四边形EFCD的周长为(??? ) www.21-cn-jy.com
A.?14?????????????????????????????????????????B.?13?????????????????????????????????????????C.?12?????????????????????????????????????????D.?10
10.如图,?ABCD的对角线AC、BD相交于点O,点E是AB的中点, 的周长是8,则 的周长为________. 【来源:21·世纪·教育·网】
11.一个平行四边形的一条边长为5,两条对角线的长分别为6和8,则它的面积为________.
12.已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF. 21·世纪*教育网
答案解析部分
一、基础夯实
1. D
平行四边形的对角相等,对角线互相平分,对边平行且相等.
故答案为:D. 分析:平行四边形的性质:对边平行且相等,对角线互相平分,对角相等,邻角互补,据此判断即可.
2. C
解:如图
∵平行四边形ABCD,
∴AO=4,BD=5
∴ 的周长=AB+AO+BO=6+4+5=15
故答案为:C
分析:首先利用平行四边形对角线互相平分得AO=4,BD=5,然后把 的周长求出.
3. D
解:∵平行四边形ABCD ∴BO=DO,故A不符合题意; ∴AB=CD,故B不符合题意; ∴∠BAD=∠BCD,故C不符合题意; AC不一定等于BD,故D符合题意; 故答案为;D 分析:利用平行四边形的对角线互相平分,可对A作出判断;根据平行四边形的对应边相等,对角相等,可对B、C作出判断;再根据平行四边形的对角线不一定相等,可对D作出判断。
4. D
如图,在平行四边形ABCD中,AB=5,
∴CD=AB=5,
∵△OCD的周长为16,
∴DO+CO=16-5=11,
故AC+BD=2(DO+CO)=22,
故答案为:D.
分析:根据题意作出图形,再根据平行四边形的性质即可求解.
5. B
∵四边形ABCD是平行四边形,
∴AB=CD=6,
∵△OCD的周长为16,
∴OD+OC=16?6=10,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=20,
故答案为:B.
分析:由平行四边形的性质可得AB=CD,OA=OC,OB=OD;再结合三角形OCD的周长=OC+OD+CD=16可求得OD+OC的长,于是AC+BD=2(OC+OD)可求解。21cnjy.com
6. A
因为在 ABCD中, AB≠AD,所以 ABCD不是菱形,所以AC⊥BD错误,
故答案为:A.
分析:平行四边形的对边平行且相等、对角相等、对角线互相平分,据此分别判断即可.
7. A
解:∵平行四边形ABCD的对角线A
C、BD相交于点O,AC+BD=24厘米,
∴AO+BO=DO+CO= ×24=12(cm),
∵△OAB的周长是18厘米,
∴AB的长为:6cm.
故答案为:A.
分析:直接利用平行四边形对角线互相平分得出AO+BO的值,进而得出答案.
8. 36
解:∵四边形ABCD是平行四边形,AB=5, ∴OB=OD=BD,OA=OC=AC,CD=AB=5, ∵△ OCD的周长 =OD+OC+CD=23, ∴OC+OD=18, 即BD+AC=18, ∴BD+AC=36. 故答案为:36. 2·1·c·n·j·y
分析:根据平行四边形的性质可得OB=OD=BD,OA=OC=AC,CD=AB=5,由△ OCD的周长 =OD+OC+CD=23,可得BD+AC=36,据此求出结论.www-2-1-cnjy-com
二、提高特训
9. C
解:∵平行四边形ABCD,周长为18 ∴OB=OD,AD∥BC,BC+CD=9 ∴∠OBF=∠ODE 在△OBF和△ODE中, ∴△OBF≌△ODE(ASA) ∴OE=OF=1.5,DE=BF ∵四边形EFCD的周长为:DE+FC+EF+CD=BF+FC+2OE+CD=BC+CD+2OE=9+2×1.5=12. 故答案为:C. 分析:利用平行四边形的性质,结合已知条件可得到OB=OD,AD∥BC,BC+CD=9,从而可证得∠OBF=∠ODE,四边形EFCD的周长再利用ASA证明△OBF≌△ODE,利用全等三角形的性质,易证OE=OF=1.5,DE=BF,然后证明四边形EFCD的周长=BC+CD+2OE,代入计算可求值。
10. 16
解:∵?ABCD的对角线AC、BD相交于点O,
,
∴O为BD中点,
∵点E是AB的中点,
∵四边形ABCD是平行四边形,
的周长为8,
的周长是16,
故答案为16.
分析:根据平行四边形的性质,对角线互相平分,又点E是AB的中点,所以 的周长是△BEO周长的两倍。2-1-c-n-j-y
11. 24
解:根据题意画出相应的图形,如图所示:
则有平行四边形ABCD中,BC=5,AC=6,BD=8,
∴OC= AC=3,OB= BD=4,
∵OC2+OB2=9+16=25,BC2=25,
∴OC2+OB2=BC2 ,
∴∠BOC=90°,即AC⊥BD,
∴四边形ABCD为菱形,
则菱形ABCD的面积S= AC?BD= ×6×8=24,
故答案为:24.
分析:利用平行四边形的对角线互相平分,分别求出OC,OB的长,再利用勾股定理的逆定理证明△BOC是直角三角形,然后根据对角线互相垂直的平行四边形是菱形,易证四边形ABCD为菱形,根据菱形的面积等于两对角线之积的一半,就可求出此菱形的面积。21*cnjy*com
12. 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF.
分析:由平行四边形的性质可得 AD∥BC,OA=OC, 由平行线的性质可得 ∠OAE=∠OCF, 然后用角边角可证 △AOE≌△COF,根据全等三角形的性质可求解。【来源:21cnj*y.co*m】
一、基础夯实
1.平行四边形所具有的性质是(?? )
A.?对角线相等???????????B.?邻边互相垂直???????????C.?每条对角线平分一组对角???????????D.?两组对边分别相等
2.在平行四边形 中,对角线 相交于点 ,若 ,则 的周长为(??? ) 21世纪教育网版权所有
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,在 ABCD中,AC与BD相交于点O,则下列结论不一定成立是( ??)
A.?BO=DO??????????????????????????B.?AB=CD??????????????????????????C.?∠BAD=∠BCD??????????????????????????D.?AC=BD
4.ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是(?? )
A.?10?????????????????????????????????????????B.?11?????????????????????????????????????????C.?12?????????????????????????????????????????D.?22
5.如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为16,则AC与BD的和是(??? )
A.?22?????????????????????????????????????????B.?20?????????????????????????????????????????C.?16?????????????????????????????????????????D.?10
6.如图所示,在□ABCD中,对角线AC、BD相交于点O , 且AB≠AD , 则下列式子错误的是()
A.?AC⊥BD?????????????????????????B.?AB=CD?????????????????????????C.?BO=OD?????????????????????????D.?∠BAD=∠BCD
7.如图,平行四边形ABCD的对角线AC、BD相交于点O , 若AC+BD=24厘米,△OAB的周长是18厘米,则AB的长为(?? ) 21教育网
A.?6厘米?????????????????????????????????B.?12厘米?????????????????????????????????C.?5厘米?????????????????????????????????D.?9厘米
8.如图, ABCD的对角线交于点O,且AB=5, OCD的周长为23,则 ABCD的两条对角线长的和是________. 21·cn·jy·com
二、提高特训
9.如图,EF过□ABCD对角线的交点O交AD于点E,交BC于点F,若□ABCD的周长为18,OE=1.5,则四边形EFCD的周长为(??? ) www.21-cn-jy.com
A.?14?????????????????????????????????????????B.?13?????????????????????????????????????????C.?12?????????????????????????????????????????D.?10
10.如图,?ABCD的对角线AC、BD相交于点O,点E是AB的中点, 的周长是8,则 的周长为________. 【来源:21·世纪·教育·网】
11.一个平行四边形的一条边长为5,两条对角线的长分别为6和8,则它的面积为________.
12.已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF. 21·世纪*教育网
答案解析部分
一、基础夯实
1. D
平行四边形的对角相等,对角线互相平分,对边平行且相等.
故答案为:D. 分析:平行四边形的性质:对边平行且相等,对角线互相平分,对角相等,邻角互补,据此判断即可.
2. C
解:如图
∵平行四边形ABCD,
∴AO=4,BD=5
∴ 的周长=AB+AO+BO=6+4+5=15
故答案为:C
分析:首先利用平行四边形对角线互相平分得AO=4,BD=5,然后把 的周长求出.
3. D
解:∵平行四边形ABCD ∴BO=DO,故A不符合题意; ∴AB=CD,故B不符合题意; ∴∠BAD=∠BCD,故C不符合题意; AC不一定等于BD,故D符合题意; 故答案为;D 分析:利用平行四边形的对角线互相平分,可对A作出判断;根据平行四边形的对应边相等,对角相等,可对B、C作出判断;再根据平行四边形的对角线不一定相等,可对D作出判断。
4. D
如图,在平行四边形ABCD中,AB=5,
∴CD=AB=5,
∵△OCD的周长为16,
∴DO+CO=16-5=11,
故AC+BD=2(DO+CO)=22,
故答案为:D.
分析:根据题意作出图形,再根据平行四边形的性质即可求解.
5. B
∵四边形ABCD是平行四边形,
∴AB=CD=6,
∵△OCD的周长为16,
∴OD+OC=16?6=10,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=20,
故答案为:B.
分析:由平行四边形的性质可得AB=CD,OA=OC,OB=OD;再结合三角形OCD的周长=OC+OD+CD=16可求得OD+OC的长,于是AC+BD=2(OC+OD)可求解。21cnjy.com
6. A
因为在 ABCD中, AB≠AD,所以 ABCD不是菱形,所以AC⊥BD错误,
故答案为:A.
分析:平行四边形的对边平行且相等、对角相等、对角线互相平分,据此分别判断即可.
7. A
解:∵平行四边形ABCD的对角线A
C、BD相交于点O,AC+BD=24厘米,
∴AO+BO=DO+CO= ×24=12(cm),
∵△OAB的周长是18厘米,
∴AB的长为:6cm.
故答案为:A.
分析:直接利用平行四边形对角线互相平分得出AO+BO的值,进而得出答案.
8. 36
解:∵四边形ABCD是平行四边形,AB=5, ∴OB=OD=BD,OA=OC=AC,CD=AB=5, ∵△ OCD的周长 =OD+OC+CD=23, ∴OC+OD=18, 即BD+AC=18, ∴BD+AC=36. 故答案为:36. 2·1·c·n·j·y
分析:根据平行四边形的性质可得OB=OD=BD,OA=OC=AC,CD=AB=5,由△ OCD的周长 =OD+OC+CD=23,可得BD+AC=36,据此求出结论.www-2-1-cnjy-com
二、提高特训
9. C
解:∵平行四边形ABCD,周长为18 ∴OB=OD,AD∥BC,BC+CD=9 ∴∠OBF=∠ODE 在△OBF和△ODE中, ∴△OBF≌△ODE(ASA) ∴OE=OF=1.5,DE=BF ∵四边形EFCD的周长为:DE+FC+EF+CD=BF+FC+2OE+CD=BC+CD+2OE=9+2×1.5=12. 故答案为:C. 分析:利用平行四边形的性质,结合已知条件可得到OB=OD,AD∥BC,BC+CD=9,从而可证得∠OBF=∠ODE,四边形EFCD的周长再利用ASA证明△OBF≌△ODE,利用全等三角形的性质,易证OE=OF=1.5,DE=BF,然后证明四边形EFCD的周长=BC+CD+2OE,代入计算可求值。
10. 16
解:∵?ABCD的对角线AC、BD相交于点O,
,
∴O为BD中点,
∵点E是AB的中点,
∵四边形ABCD是平行四边形,
的周长为8,
的周长是16,
故答案为16.
分析:根据平行四边形的性质,对角线互相平分,又点E是AB的中点,所以 的周长是△BEO周长的两倍。2-1-c-n-j-y
11. 24
解:根据题意画出相应的图形,如图所示:
则有平行四边形ABCD中,BC=5,AC=6,BD=8,
∴OC= AC=3,OB= BD=4,
∵OC2+OB2=9+16=25,BC2=25,
∴OC2+OB2=BC2 ,
∴∠BOC=90°,即AC⊥BD,
∴四边形ABCD为菱形,
则菱形ABCD的面积S= AC?BD= ×6×8=24,
故答案为:24.
分析:利用平行四边形的对角线互相平分,分别求出OC,OB的长,再利用勾股定理的逆定理证明△BOC是直角三角形,然后根据对角线互相垂直的平行四边形是菱形,易证四边形ABCD为菱形,根据菱形的面积等于两对角线之积的一半,就可求出此菱形的面积。21*cnjy*com
12. 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF.
分析:由平行四边形的性质可得 AD∥BC,OA=OC, 由平行线的性质可得 ∠OAE=∠OCF, 然后用角边角可证 △AOE≌△COF,根据全等三角形的性质可求解。【来源:21cnj*y.co*m】
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
