2020年浙教版八年级数学下册4.2 平行四边形及其性质 同步练习(1)(含答案)
文档属性
| 名称 | 2020年浙教版八年级数学下册4.2 平行四边形及其性质 同步练习(1)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 149.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 22:31:56 | ||
图片预览



文档简介
4.2 平行四边形及其性质(第1课时)
课堂笔记
1. 定义:两组对边分别平行的四边形叫做________ .
2. 性质:平行四边形的对边________ . 平行四边形的对角________.
分层训练
A组 基础训练
1. ABCD的四个内角的度数之比∠A∶∠B∶∠C∶∠D可能是( )
A. 2∶5∶2∶5 B. 3∶4∶4∶3 C. 4∶4∶2∶2 D. 2∶3∶4∶5
2. 如图,在ABCD中,若∠B=60°,AB=5cm,则以下结论正确的是( )
A. BC=5cm,∠D=60°
B. ∠C=120°,CD=5cm
C. AD=5cm,∠A=60°
D. ∠A=120°,AD=5cm
3. 已知平行四边形的周长为20cm,两邻边之比为3∶2,则较长边的长为( )
A. 6cm B. 4cm C. 3cm D. 2cm
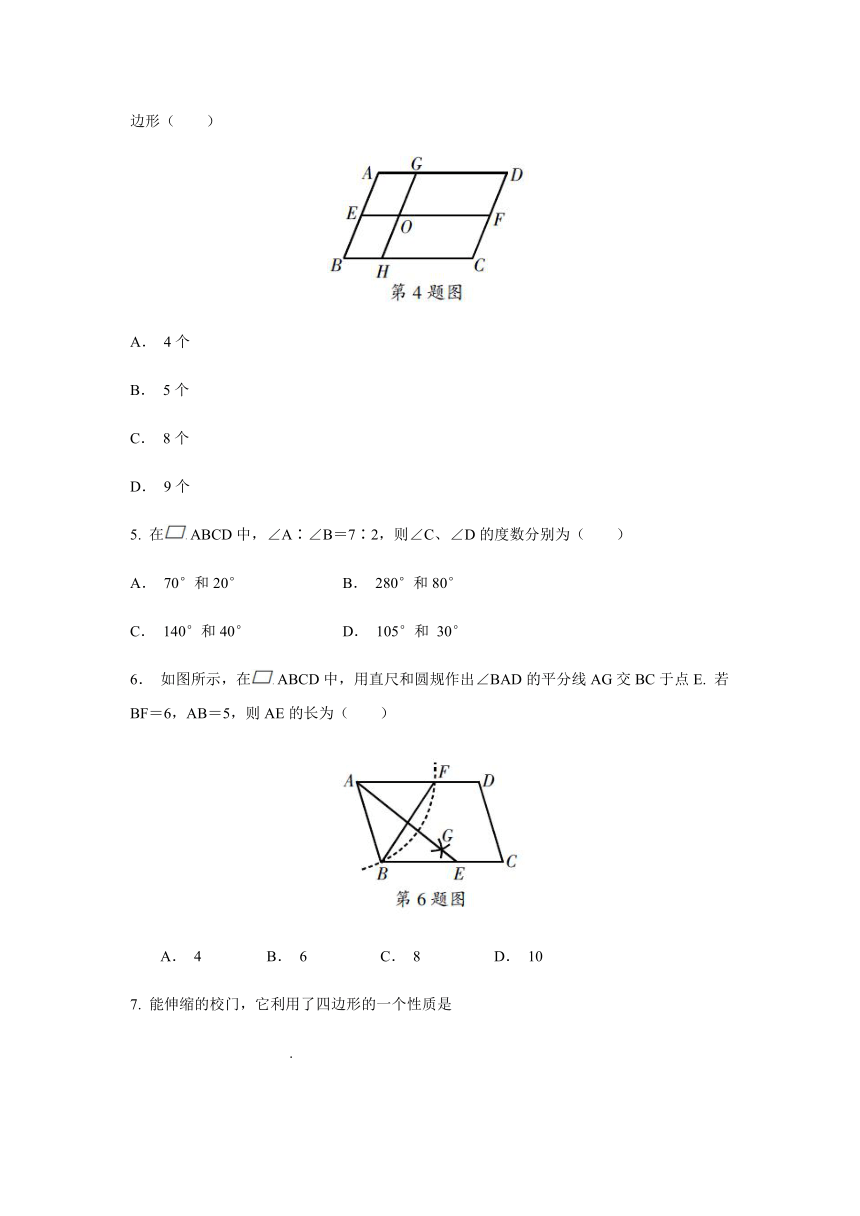
4. 如图,在ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中共有平行四边形( )
A. 4个
B. 5个
C. 8个
D. 9个
5. 在ABCD中,∠A∶∠B=7∶2,则∠C、∠D的度数分别为( )
A. 70°和20° B. 280°和80°
C. 140°和40° D. 105°和 30°
6. 如图所示,在ABCD中,用直尺和圆规作出∠BAD的平分线AG交BC于点E. 若BF=6,AB=5,则AE的长为( )
A. 4 B. 6 C. 8 D. 10
7. 能伸缩的校门,它利用了四边形的一个性质是
.
8. 在ABCD中,∠A=48°,BC=3cm,则∠B=________,AD=________.
9. 已知平行四边形的最大角比最小角大70°,则最大角为________°.
10. 如图,在ABCD中,DE⊥AB于点E,DF⊥BC于点F,且∠ADE+∠CDF=60°,则∠EDF的度数是________ .
11. 如图所示,在ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE∶EC=1∶2,则∠BCD的度数为________ .
12. 如图,四边形ABCD中,E是BC边的中点,连结DE并延长交AB的延长线于点F,已知AD=4,AB=BF,∠F=∠CDE. 求BC的长.
B组 自主提高
13. 如图,在ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为________ .
14. 如图,四边形ABCD是平行四边形,且∠EAD=∠BAF.
(1)△CEF是等腰三角形吗?请你说明其中的道理;
(2)想一想:△CEF的哪两条边之和等于ABCD的周长,并说明理由.
15. 如图,在平行四边形ABCD中,点E是BC上的一点,F在线段DE上,且∠AFE=∠ADC.
(1)若∠AFE=70°,∠DEC=40°,求∠DAF的大小;
(2)若DE=AD,求证:△AFD≌△DCE.
C组 综合运用
16. 如图,已知ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)试说明线段CD与FA相等的理由;
(2)若使∠F=∠BCF,ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).
参考答案
【课堂笔记】
1. 平行四边形
2. 相等 相等
【分层训练】
1—5. ABADC 6. C
7. 四边形的不稳定性
8. 132° 3cm
9. 125
10. 60°
11. 120°
12. ∵∠CDE=∠F,∴CD∥BF,又∵E是BC的中点,∴EC=EB,在△DEC与△FEB中,∴△DEC≌△FEB(AAS),∴CD=BF,∴AB=CD,又∵DC∥BF,∴四边形ABCD是平行四边形,∴BC=AD=4.
13. 21° 【点拨】设∠ADE=x,∵AE=EF,∠ADF=90°,∴DE=AF=AE=EF,∠DAE=∠ADE=x,∵AE=EF=CD,∴DE=CD,∴∠DCE=∠DEC=2x,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠BCA=x,∴∠DCE=∠BCD-∠BCA=63°-x,∴2x=63°-x,解得:x=21°,即∠ADE=21°.
14. (1)△CEF是等腰三角形,∵ABCD,∴AD∥BC,AB∥CE,∴∠EAD=∠F,∠FAB=∠E. ∵∠EAD=∠BAF,∴∠E=∠F,∴△CEF是等腰三角形;
(2)∵∠E=∠F=∠FAB=∠EAD,∴BF=BA,DA=DE. ∴AB+AD+CD+CB=FC+EC.
15. (1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADF=∠DEC=40°. ∵∠AFD+∠AFE=180°,∴∠AFD=180°-∠AFE=110°,∴∠DAF=180°-∠ADF-∠AFD=30°;
(2)∵四边形ABCD是平行四边形,∴∠B=∠ADC,AB∥CD,AD∥BC,∴∠C+∠ADC=180°,∠ADF=∠DEC,∵∠AFD+∠AFE=180°,∠AFE=∠ADC,∴∠AFD=∠C,在△AFD和△DCE中,∴△AFD≌△DCE(AAS).
16. (1)∵四边形ABCD是平行四边形,∴CD∥AB,又∵CE的延长线交BA的延长线于点F,∴∠CDA=∠DAF,∵E是AD中点,∴DE=AE,∵∠CED=∠AEF,∴△CDE≌△FAE,∴CD=FA.
(2)要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB.
理由:∵由(1)知,△CED≌△FEA,∴CD=FA,又∵四边形ABCD是平行四边形,∴CD=AB,∴AB=AF,即BF=2AB,∵BC=2AB,∴BF=BC,∴∠F=∠BCF.
课堂笔记
1. 定义:两组对边分别平行的四边形叫做________ .
2. 性质:平行四边形的对边________ . 平行四边形的对角________.
分层训练
A组 基础训练
1. ABCD的四个内角的度数之比∠A∶∠B∶∠C∶∠D可能是( )
A. 2∶5∶2∶5 B. 3∶4∶4∶3 C. 4∶4∶2∶2 D. 2∶3∶4∶5
2. 如图,在ABCD中,若∠B=60°,AB=5cm,则以下结论正确的是( )
A. BC=5cm,∠D=60°
B. ∠C=120°,CD=5cm
C. AD=5cm,∠A=60°
D. ∠A=120°,AD=5cm
3. 已知平行四边形的周长为20cm,两邻边之比为3∶2,则较长边的长为( )
A. 6cm B. 4cm C. 3cm D. 2cm
4. 如图,在ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中共有平行四边形( )
A. 4个
B. 5个
C. 8个
D. 9个
5. 在ABCD中,∠A∶∠B=7∶2,则∠C、∠D的度数分别为( )
A. 70°和20° B. 280°和80°
C. 140°和40° D. 105°和 30°
6. 如图所示,在ABCD中,用直尺和圆规作出∠BAD的平分线AG交BC于点E. 若BF=6,AB=5,则AE的长为( )
A. 4 B. 6 C. 8 D. 10
7. 能伸缩的校门,它利用了四边形的一个性质是
.
8. 在ABCD中,∠A=48°,BC=3cm,则∠B=________,AD=________.
9. 已知平行四边形的最大角比最小角大70°,则最大角为________°.
10. 如图,在ABCD中,DE⊥AB于点E,DF⊥BC于点F,且∠ADE+∠CDF=60°,则∠EDF的度数是________ .
11. 如图所示,在ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE∶EC=1∶2,则∠BCD的度数为________ .
12. 如图,四边形ABCD中,E是BC边的中点,连结DE并延长交AB的延长线于点F,已知AD=4,AB=BF,∠F=∠CDE. 求BC的长.
B组 自主提高
13. 如图,在ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为________ .
14. 如图,四边形ABCD是平行四边形,且∠EAD=∠BAF.
(1)△CEF是等腰三角形吗?请你说明其中的道理;
(2)想一想:△CEF的哪两条边之和等于ABCD的周长,并说明理由.
15. 如图,在平行四边形ABCD中,点E是BC上的一点,F在线段DE上,且∠AFE=∠ADC.
(1)若∠AFE=70°,∠DEC=40°,求∠DAF的大小;
(2)若DE=AD,求证:△AFD≌△DCE.
C组 综合运用
16. 如图,已知ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)试说明线段CD与FA相等的理由;
(2)若使∠F=∠BCF,ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).
参考答案
【课堂笔记】
1. 平行四边形
2. 相等 相等
【分层训练】
1—5. ABADC 6. C
7. 四边形的不稳定性
8. 132° 3cm
9. 125
10. 60°
11. 120°
12. ∵∠CDE=∠F,∴CD∥BF,又∵E是BC的中点,∴EC=EB,在△DEC与△FEB中,∴△DEC≌△FEB(AAS),∴CD=BF,∴AB=CD,又∵DC∥BF,∴四边形ABCD是平行四边形,∴BC=AD=4.
13. 21° 【点拨】设∠ADE=x,∵AE=EF,∠ADF=90°,∴DE=AF=AE=EF,∠DAE=∠ADE=x,∵AE=EF=CD,∴DE=CD,∴∠DCE=∠DEC=2x,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠BCA=x,∴∠DCE=∠BCD-∠BCA=63°-x,∴2x=63°-x,解得:x=21°,即∠ADE=21°.
14. (1)△CEF是等腰三角形,∵ABCD,∴AD∥BC,AB∥CE,∴∠EAD=∠F,∠FAB=∠E. ∵∠EAD=∠BAF,∴∠E=∠F,∴△CEF是等腰三角形;
(2)∵∠E=∠F=∠FAB=∠EAD,∴BF=BA,DA=DE. ∴AB+AD+CD+CB=FC+EC.
15. (1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADF=∠DEC=40°. ∵∠AFD+∠AFE=180°,∴∠AFD=180°-∠AFE=110°,∴∠DAF=180°-∠ADF-∠AFD=30°;
(2)∵四边形ABCD是平行四边形,∴∠B=∠ADC,AB∥CD,AD∥BC,∴∠C+∠ADC=180°,∠ADF=∠DEC,∵∠AFD+∠AFE=180°,∠AFE=∠ADC,∴∠AFD=∠C,在△AFD和△DCE中,∴△AFD≌△DCE(AAS).
16. (1)∵四边形ABCD是平行四边形,∴CD∥AB,又∵CE的延长线交BA的延长线于点F,∴∠CDA=∠DAF,∵E是AD中点,∴DE=AE,∵∠CED=∠AEF,∴△CDE≌△FAE,∴CD=FA.
(2)要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB.
理由:∵由(1)知,△CED≌△FEA,∴CD=FA,又∵四边形ABCD是平行四边形,∴CD=AB,∴AB=AF,即BF=2AB,∵BC=2AB,∴BF=BC,∴∠F=∠BCF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
