2020年浙教版八年级数学下册4.2 平行四边形及其性质 同步练习(2)(含答案)
文档属性
| 名称 | 2020年浙教版八年级数学下册4.2 平行四边形及其性质 同步练习(2)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 131.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览



文档简介
4.2 平行四边形及其性质(第2课时)
课堂笔记
1. 平行线性质:夹在两条平行线间的________相等,夹在________间的垂线段相等.
2. 平行线之间距离:两条平行线中,一条直线上的点到另一条直线的距离,叫做这两条________.
分层训练
A组 基础训练
1. 如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( )
A. S四边形ABCD=S四边形ECDF
B. S四边形ABCD<S四边形ECDF
C. S四边形ABCD=S四边形ECDF+1
D. S四边形ABCD=S四边形ECDF+2
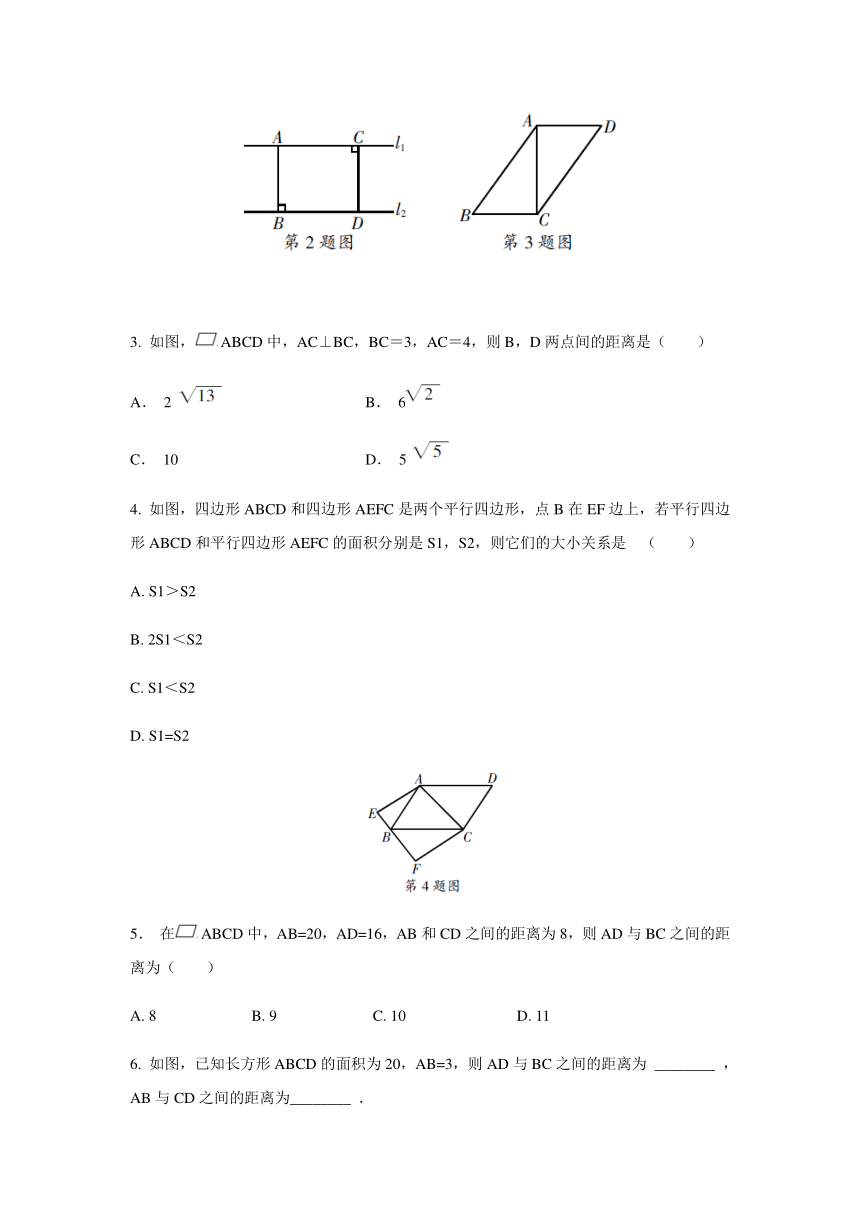
2. 如图,l1∥l2,AB⊥l2,CD⊥l1,则下列结论正确的有( )
①AB⊥l1;②AB∥CD;③AB=CD;④AC=BD.
A. 4个 B. 3个 C. 2个 D. 1个
3. 如图,ABCD中,AC⊥BC,BC=3,AC=4,则B,D两点间的距离是( )
A. 2 B. 6
C. 10 D. 5
4. 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是S1,S2,则它们的大小关系是 ( )
A. S1>S2
B. 2S1<S2
C. S1<S2
D. S1=S2
5. 在ABCD中,AB=20,AD=16,AB和CD之间的距离为8,则AD与BC之间的距离为( )
A. 8 B. 9 C. 10 D. 11
6. 如图,已知长方形ABCD的面积为20,AB=3,则AD与BC之间的距离为 ________ ,AB与CD之间的距离为________ .
7. 如图,ABCD中,AB=6,BC=4,若∠B=45°,则ABCD的面积为________ .
8. 已知直线a,b,c在同一平面内,且a∥b∥c,若a与c的距离为3cm,b与c的距离为2cm,则a与b的距离为 ________ .
9. 如图,如果直线l1∥l2,那么△ABC的面积与△DBC的面积相等吗?如果相等,请说明理由.
在图中你还能得到哪些面积相等的结论?你还能在平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?这样的三角形能画出多少个?
10. 如图,在ABCD中,AE⊥CD,AF⊥BC,垂足分别为E,F,∠EAF=60°,CE=1,CF=4. 求ABCD的各边长.
B组 自主提高
11. 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是( )
A. B. C. 5 D. 10
12. (南充中考)如图,在ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则SAEPH=________ .
13. 如图所示,在ABCD中,点E是DC边上一点,连结AE,BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.
(1)求证:AE⊥BE;
(2)若AE=3,BE=2,求ABCD的面积.
C组 综合运用
14. 已知线段y=-x+a(1≤x≤3),当a的值由-1增加到2时,求线段运动所经过的平面区域的面积.
参考答案
【课堂笔记】
1. 平行线段 两条平行线
2. 平行线之间的距离
【分层训练】
1—5. AAADC
6. 3
7. 12
8. 5cm或1cm
9. △ABC的面积与△DBC的面积相等. 理由如下:∵l1∥l2,点A、点D都在直线l1上,∴点A、点D到直线l2的距离相等. ∵BC在直线l2上,∴△ABC与△DBC是同底等高的两个三角形,∴△ABC的面积等于△DBC的面积. 在图中面积相等的三角形还有:△BAD的面积等于△CAD的面积;△AOB的面积等于△DOC的面积. 在这两条平行线l1与l2之间能画出其他的与△ABC面积相等的三角形. 在直线l1上任取一点E(点E不与点A重合),如图,连结EB,EC,
△EBC的面积等于△ABC的面积. 这样的三角形能画出无数个.
10. AB=CD=4,BC=AD=6.
11. A
12. 4
13. (1)证明:∵ABCD,∴AD∥BC,∴∠DAB+∠CBA=180°,又∵AE是∠DAB的平分线,∴∠EAB=∠DAB,同理:∠EBA=∠CBA,∴∠EAB+∠EBA=(∠DAB+∠CBA)=×180°=90°,∴∠AEB=90°,即AE⊥BE.
(2)S△ABE=3,∴SABCD=2S△ABE=6.
14. 如图,当a=-1时,y=-x-1;当a=2时,y=-x+2. ∵一次项系数都是-,∴AD∥BC. 当x=1时,y=-x-1=-,∴点B的坐标是(1,-).
同理可求得点A的坐标是(1,),点C的坐标是(3,-),点D的坐标是(3,),∴AB∥CD,∴ABCD的面积是AB·(3-1)=()×2=6.
课堂笔记
1. 平行线性质:夹在两条平行线间的________相等,夹在________间的垂线段相等.
2. 平行线之间距离:两条平行线中,一条直线上的点到另一条直线的距离,叫做这两条________.
分层训练
A组 基础训练
1. 如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( )
A. S四边形ABCD=S四边形ECDF
B. S四边形ABCD<S四边形ECDF
C. S四边形ABCD=S四边形ECDF+1
D. S四边形ABCD=S四边形ECDF+2
2. 如图,l1∥l2,AB⊥l2,CD⊥l1,则下列结论正确的有( )
①AB⊥l1;②AB∥CD;③AB=CD;④AC=BD.
A. 4个 B. 3个 C. 2个 D. 1个
3. 如图,ABCD中,AC⊥BC,BC=3,AC=4,则B,D两点间的距离是( )
A. 2 B. 6
C. 10 D. 5
4. 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是S1,S2,则它们的大小关系是 ( )
A. S1>S2
B. 2S1<S2
C. S1<S2
D. S1=S2
5. 在ABCD中,AB=20,AD=16,AB和CD之间的距离为8,则AD与BC之间的距离为( )
A. 8 B. 9 C. 10 D. 11
6. 如图,已知长方形ABCD的面积为20,AB=3,则AD与BC之间的距离为 ________ ,AB与CD之间的距离为________ .
7. 如图,ABCD中,AB=6,BC=4,若∠B=45°,则ABCD的面积为________ .
8. 已知直线a,b,c在同一平面内,且a∥b∥c,若a与c的距离为3cm,b与c的距离为2cm,则a与b的距离为 ________ .
9. 如图,如果直线l1∥l2,那么△ABC的面积与△DBC的面积相等吗?如果相等,请说明理由.
在图中你还能得到哪些面积相等的结论?你还能在平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?这样的三角形能画出多少个?
10. 如图,在ABCD中,AE⊥CD,AF⊥BC,垂足分别为E,F,∠EAF=60°,CE=1,CF=4. 求ABCD的各边长.
B组 自主提高
11. 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是( )
A. B. C. 5 D. 10
12. (南充中考)如图,在ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则SAEPH=________ .
13. 如图所示,在ABCD中,点E是DC边上一点,连结AE,BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.
(1)求证:AE⊥BE;
(2)若AE=3,BE=2,求ABCD的面积.
C组 综合运用
14. 已知线段y=-x+a(1≤x≤3),当a的值由-1增加到2时,求线段运动所经过的平面区域的面积.
参考答案
【课堂笔记】
1. 平行线段 两条平行线
2. 平行线之间的距离
【分层训练】
1—5. AAADC
6. 3
7. 12
8. 5cm或1cm
9. △ABC的面积与△DBC的面积相等. 理由如下:∵l1∥l2,点A、点D都在直线l1上,∴点A、点D到直线l2的距离相等. ∵BC在直线l2上,∴△ABC与△DBC是同底等高的两个三角形,∴△ABC的面积等于△DBC的面积. 在图中面积相等的三角形还有:△BAD的面积等于△CAD的面积;△AOB的面积等于△DOC的面积. 在这两条平行线l1与l2之间能画出其他的与△ABC面积相等的三角形. 在直线l1上任取一点E(点E不与点A重合),如图,连结EB,EC,
△EBC的面积等于△ABC的面积. 这样的三角形能画出无数个.
10. AB=CD=4,BC=AD=6.
11. A
12. 4
13. (1)证明:∵ABCD,∴AD∥BC,∴∠DAB+∠CBA=180°,又∵AE是∠DAB的平分线,∴∠EAB=∠DAB,同理:∠EBA=∠CBA,∴∠EAB+∠EBA=(∠DAB+∠CBA)=×180°=90°,∴∠AEB=90°,即AE⊥BE.
(2)S△ABE=3,∴SABCD=2S△ABE=6.
14. 如图,当a=-1时,y=-x-1;当a=2时,y=-x+2. ∵一次项系数都是-,∴AD∥BC. 当x=1时,y=-x-1=-,∴点B的坐标是(1,-).
同理可求得点A的坐标是(1,),点C的坐标是(3,-),点D的坐标是(3,),∴AB∥CD,∴ABCD的面积是AB·(3-1)=()×2=6.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
