浙教版数学八年级下册 3.1 平均数 同步练习(含答案)
文档属性
| 名称 | 浙教版数学八年级下册 3.1 平均数 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-31 00:00:00 | ||
图片预览




文档简介
第3章 数据分析初步 3.1 平均数
1.已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+5,a2-5,a3+5,a4-5,a5+5的平均数为( )
A. 8 B. 9 10. 10 D.11
2. 一组数据:40、37、x、64的平均数是53,则x的值是( )
A. 67 B. 69 C. 71 D. 72
3.在一次青年歌手大奖赛上,七位评委为某位歌手打出的分数如下:9.5, 9.4, 9.6, 9.9, 9.3, 9.7,9.0,去掉一个最高分和一个最低分后,所剩数据的平均数是( )
A.9.2 B.9.3 C.9.4 D.9.5
4. 有一组数据:2,5,5,6,7,这组数据的平均数为( )
A.3 B.4 C.5 D.6
5. 某学校生物兴趣小组11人到校外采集植物标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个兴趣小组平均每人采集标本是( )
A.3件 B.4件 C.5件 D.6件
6. 已知一组数据1,7,10,8,a,6,0,3,若x=5,则a应等于( )
A.6 B.5 C.4 D.3
7. 为了满足顾客的需求,某商场将5 kg奶糖,3 kg酥心糖和2 kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后的什锦糖的售价应为每千克( )
A.25元 B.28.5元 C.29元 D.34.5元
8. 如图是小芹6月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
A.1小时 B.1.5小时 C.2小时 D.3小时
9. 某地区100个家庭收入按从低到高是5800元,…,10000元,各不相同,在输入计算机时,把最大的数错误地输成100000元,则依据错误数字算出的平均值与实际数字的平均值的差是( )
A.900元 B.942元 C.90000元 D.1000元
10. 某校规定学生的这学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分 B.82分 C.84分 D.86分
11. 如果一组数据6,x, 2, 4的平均数为5,那么x为
12. 某班40名学生的某次体育素质测验成绩统计表如下:
成绩(分) 50 60 70 80 90 100
人数(人) 2 x 10 y 8 2
若这个班的体育素质平均成绩是74分,则x=____,y=____.
13. 学校把学生的笔试、实践能力两项成绩分别按60%,40%的比例计入学期总成绩.小明实践能力这一项成绩是81分,若他想学期总成绩达到90分,则他笔试的成绩必须达到________分.
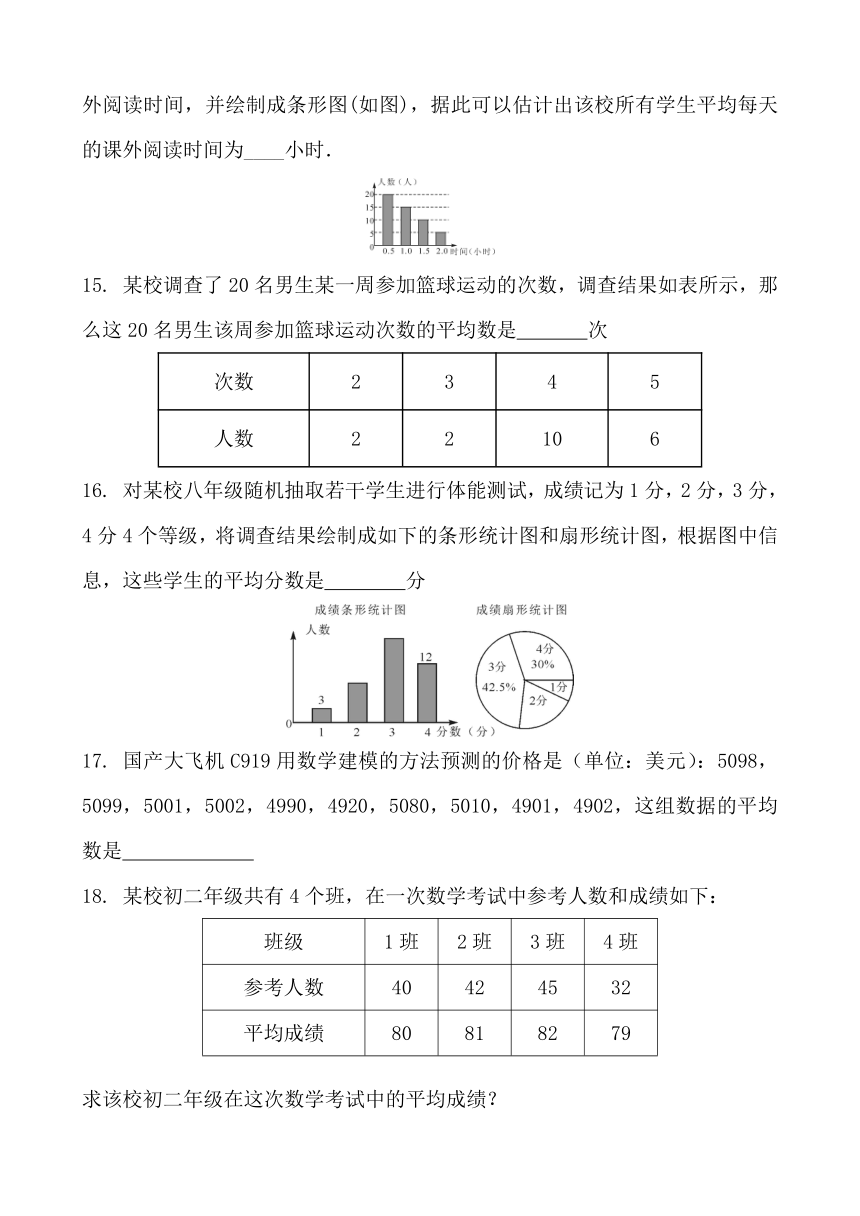
14. 某校为了了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图(如图),据此可以估计出该校所有学生平均每天的课外阅读时间为____小时.
15. 某校调查了20名男生某一周参加篮球运动的次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是 次
次数 2 3 4 5
人数 2 2 10 6
16. 对某校八年级随机抽取若干学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下的条形统计图和扇形统计图,根据图中信息,这些学生的平均分数是 分
17. 国产大飞机C919用数学建模的方法预测的价格是(单位:美元):5098,5099,5001,5002,4990,4920,5080,5010,4901,4902,这组数据的平均数是
18. 某校初二年级共有4个班,在一次数学考试中参考人数和成绩如下:
班级 1班 2班 3班 4班
参考人数 40 42 45 32
平均成绩 80 81 82 79
求该校初二年级在这次数学考试中的平均成绩?
19. 某校开展“节约每一滴水”活动,为了了解开展活动的一个月以来节约用水的病况,从八年级的400名同学中选出20名同学统计了解各自家庭一个月的节水情况,见下表:
节水量/m3 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估算这400名同学的家庭一个月节约用水的总量大约是多少?
20. 一次数学测验,八年级(1)班第一学习小组有2个同学得分在70~75之间,有5个同学得分在80~85之间,有4个同学得分在85~90之间,有1个同学得分在90~95间.请估计这个班的平均成绩是多少?
21. 某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期 一 二 三 四 五 六 日
增减/辆 8 5 -2 -7 -6 10 13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
22. 某公司对应聘者进行面试,按专业知识、工作经验、仪表形象给应聘者打分,这三个方面的重要性之比为6∶3∶1.对应聘的明明、芳芳两人的打分如下表:
明明 芳芳
专业知识 14 18
工作经验 16 16
仪表形象 18 12
如果两人中只能录取一人,假若你是人事主管,根据上面的信息,你会录用谁?
23. 下表是某居民小区五月份的用水情况:
月用水量(m3) 4 5 6 8 9 11
户数 2 3 7 5 2 1
(1)计算这20户家庭的月平均用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少立方米?
24. 学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如下表:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2,1,3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
25. 甲、乙两人两次同时在同一粮站购买粮食(假设两次购买粮食的单价不同),甲每次购买粮食100 kg,乙每次购买粮食用去100元.设甲、乙两人第一次购买粮食的单价为每千克x元,第二次购买粮食的单价为每千克y元.
(1)用含x,y的代数式表示甲两次购买粮食共需付款________元,乙两次共购买________千克粮食.若甲两次购买粮食的平均单价为每千克Q1元,乙两次购买粮食的平均单价为每千克Q2元,则Q1=________元,Q2=________元;
(2)若规定两次购买粮食的平均单价较低者,购买粮食的方式是合算的.请你判断甲、乙两人购买粮食的方式哪一个更合算些,并说明理由.
26. 某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如表所示:
测试项目 测试成绩/分
甲 乙 丙
笔试 92 90 95
面试 85 95 80
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2∶5∶3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
参考答案:
1---10 BCDCB BCBAD
11. 8
12. 10 8
13. 96
14. 1
15. 4
16. 2.95
17. 5000.3
18. 解:平均成绩==80.6
19. 解:根据表格可求得所选出的20名同学平均每家一个月的节水量:(0.2×2+0.25×4+0.3×6+0.4×7+0.5×1)÷20=0.325(m3),所以400名家庭一个月节约用水的总量大约为400×0.325=130(m3).
20. 解:组中值分别为:=72.5,=82.5 =87.5,=92.5.
平均成绩为:===83.3
答:这个班的平均成绩约是83.3分.
21. 解:(1)从统计表格中得出星期四经过红绿灯路口的小汽车最少,为93辆;星期日经过红绿灯路口的小汽车最多,为113辆
(2)平均数=(8+5-2-7-6+10+13)÷7+100=103,
故平均每天有103辆小汽车通过这个红绿灯路口
22. 解:依题意,得明明的最后成绩为:=15(分),
芳芳的最后成绩为:=16.8(分),
显然由于芳芳的最后得数比明明的最后得分高,所以应录用芳芳.
23. (1) (4×2+5×3+6×7+8×5+9×2+11×1)÷20=6.7(m3).
故这20户家庭的月平均用水量为6.7m3 .
(2) 6.7×500=3350(m3).
故该小区居民每月共用水3350m3.
24. 解:(1)乙的平均成绩:=79.5,
∵80.25>79.5,∴应选派甲
(2)甲的平均成绩:=79.5,
乙的平均成绩:=80.4,
∵79.5<80.4,∴应选派乙
25. (1)(100x+100y)
(2)Q1-Q2=-=>0,
故Q1>Q2,所以乙的购买方式合算.
26. 解:(1)图略
(2)甲的票数是:200×34%=68(票),乙的票数是:200×30%=60(票),丙的票数是:200×28%=56(票)
(3)甲的平均成绩:x1==85.1,
乙的平均成绩:x2==85.5,
丙的平均成绩:x3==82.7,
∵乙的平均成绩最高,∴应该录取乙
1.已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+5,a2-5,a3+5,a4-5,a5+5的平均数为( )
A. 8 B. 9 10. 10 D.11
2. 一组数据:40、37、x、64的平均数是53,则x的值是( )
A. 67 B. 69 C. 71 D. 72
3.在一次青年歌手大奖赛上,七位评委为某位歌手打出的分数如下:9.5, 9.4, 9.6, 9.9, 9.3, 9.7,9.0,去掉一个最高分和一个最低分后,所剩数据的平均数是( )
A.9.2 B.9.3 C.9.4 D.9.5
4. 有一组数据:2,5,5,6,7,这组数据的平均数为( )
A.3 B.4 C.5 D.6
5. 某学校生物兴趣小组11人到校外采集植物标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个兴趣小组平均每人采集标本是( )
A.3件 B.4件 C.5件 D.6件
6. 已知一组数据1,7,10,8,a,6,0,3,若x=5,则a应等于( )
A.6 B.5 C.4 D.3
7. 为了满足顾客的需求,某商场将5 kg奶糖,3 kg酥心糖和2 kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后的什锦糖的售价应为每千克( )
A.25元 B.28.5元 C.29元 D.34.5元
8. 如图是小芹6月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
A.1小时 B.1.5小时 C.2小时 D.3小时
9. 某地区100个家庭收入按从低到高是5800元,…,10000元,各不相同,在输入计算机时,把最大的数错误地输成100000元,则依据错误数字算出的平均值与实际数字的平均值的差是( )
A.900元 B.942元 C.90000元 D.1000元
10. 某校规定学生的这学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分 B.82分 C.84分 D.86分
11. 如果一组数据6,x, 2, 4的平均数为5,那么x为
12. 某班40名学生的某次体育素质测验成绩统计表如下:
成绩(分) 50 60 70 80 90 100
人数(人) 2 x 10 y 8 2
若这个班的体育素质平均成绩是74分,则x=____,y=____.
13. 学校把学生的笔试、实践能力两项成绩分别按60%,40%的比例计入学期总成绩.小明实践能力这一项成绩是81分,若他想学期总成绩达到90分,则他笔试的成绩必须达到________分.
14. 某校为了了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图(如图),据此可以估计出该校所有学生平均每天的课外阅读时间为____小时.
15. 某校调查了20名男生某一周参加篮球运动的次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是 次
次数 2 3 4 5
人数 2 2 10 6
16. 对某校八年级随机抽取若干学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下的条形统计图和扇形统计图,根据图中信息,这些学生的平均分数是 分
17. 国产大飞机C919用数学建模的方法预测的价格是(单位:美元):5098,5099,5001,5002,4990,4920,5080,5010,4901,4902,这组数据的平均数是
18. 某校初二年级共有4个班,在一次数学考试中参考人数和成绩如下:
班级 1班 2班 3班 4班
参考人数 40 42 45 32
平均成绩 80 81 82 79
求该校初二年级在这次数学考试中的平均成绩?
19. 某校开展“节约每一滴水”活动,为了了解开展活动的一个月以来节约用水的病况,从八年级的400名同学中选出20名同学统计了解各自家庭一个月的节水情况,见下表:
节水量/m3 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估算这400名同学的家庭一个月节约用水的总量大约是多少?
20. 一次数学测验,八年级(1)班第一学习小组有2个同学得分在70~75之间,有5个同学得分在80~85之间,有4个同学得分在85~90之间,有1个同学得分在90~95间.请估计这个班的平均成绩是多少?
21. 某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期 一 二 三 四 五 六 日
增减/辆 8 5 -2 -7 -6 10 13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
22. 某公司对应聘者进行面试,按专业知识、工作经验、仪表形象给应聘者打分,这三个方面的重要性之比为6∶3∶1.对应聘的明明、芳芳两人的打分如下表:
明明 芳芳
专业知识 14 18
工作经验 16 16
仪表形象 18 12
如果两人中只能录取一人,假若你是人事主管,根据上面的信息,你会录用谁?
23. 下表是某居民小区五月份的用水情况:
月用水量(m3) 4 5 6 8 9 11
户数 2 3 7 5 2 1
(1)计算这20户家庭的月平均用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少立方米?
24. 学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如下表:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2,1,3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
25. 甲、乙两人两次同时在同一粮站购买粮食(假设两次购买粮食的单价不同),甲每次购买粮食100 kg,乙每次购买粮食用去100元.设甲、乙两人第一次购买粮食的单价为每千克x元,第二次购买粮食的单价为每千克y元.
(1)用含x,y的代数式表示甲两次购买粮食共需付款________元,乙两次共购买________千克粮食.若甲两次购买粮食的平均单价为每千克Q1元,乙两次购买粮食的平均单价为每千克Q2元,则Q1=________元,Q2=________元;
(2)若规定两次购买粮食的平均单价较低者,购买粮食的方式是合算的.请你判断甲、乙两人购买粮食的方式哪一个更合算些,并说明理由.
26. 某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如表所示:
测试项目 测试成绩/分
甲 乙 丙
笔试 92 90 95
面试 85 95 80
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2∶5∶3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
参考答案:
1---10 BCDCB BCBAD
11. 8
12. 10 8
13. 96
14. 1
15. 4
16. 2.95
17. 5000.3
18. 解:平均成绩==80.6
19. 解:根据表格可求得所选出的20名同学平均每家一个月的节水量:(0.2×2+0.25×4+0.3×6+0.4×7+0.5×1)÷20=0.325(m3),所以400名家庭一个月节约用水的总量大约为400×0.325=130(m3).
20. 解:组中值分别为:=72.5,=82.5 =87.5,=92.5.
平均成绩为:===83.3
答:这个班的平均成绩约是83.3分.
21. 解:(1)从统计表格中得出星期四经过红绿灯路口的小汽车最少,为93辆;星期日经过红绿灯路口的小汽车最多,为113辆
(2)平均数=(8+5-2-7-6+10+13)÷7+100=103,
故平均每天有103辆小汽车通过这个红绿灯路口
22. 解:依题意,得明明的最后成绩为:=15(分),
芳芳的最后成绩为:=16.8(分),
显然由于芳芳的最后得数比明明的最后得分高,所以应录用芳芳.
23. (1) (4×2+5×3+6×7+8×5+9×2+11×1)÷20=6.7(m3).
故这20户家庭的月平均用水量为6.7m3 .
(2) 6.7×500=3350(m3).
故该小区居民每月共用水3350m3.
24. 解:(1)乙的平均成绩:=79.5,
∵80.25>79.5,∴应选派甲
(2)甲的平均成绩:=79.5,
乙的平均成绩:=80.4,
∵79.5<80.4,∴应选派乙
25. (1)(100x+100y)
(2)Q1-Q2=-=>0,
故Q1>Q2,所以乙的购买方式合算.
26. 解:(1)图略
(2)甲的票数是:200×34%=68(票),乙的票数是:200×30%=60(票),丙的票数是:200×28%=56(票)
(3)甲的平均成绩:x1==85.1,
乙的平均成绩:x2==85.5,
丙的平均成绩:x3==82.7,
∵乙的平均成绩最高,∴应该录取乙
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
