5.1.1 矩形的性质同步练习（含答案）

中小学教育资源及组卷应用平台


5.1　矩形
第1课时　矩形的性质　 　　　　　

知识点1　矩形的定义
1.如图5-1-1,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形.
求证:四边形ADBE是矩形.

图5-1-1

知识点2　矩形边、角的性质
2.矩形ABCD的两邻边长分别是1,2,则BD的长是 (　　)
A. B.3 C. D.2
3.四边形ABCD为矩形,已知点A(1,1),B(3,1),C(3,5),那么点D的坐标为 (　　)
A.(1,3) B.(1,5) C.(5,3) D.(5,1)
4.如图5-1-2,矩形ABCD的周长是28,O是AC的中点,P是AD的中点,△AOD的周长与△COD的周长差是2(且AD>CD),则△AOP的周长为 (　　)

图5-1-2
A.12 B.14 C.16 D.18
5.如图5-1-3,直线l∥m,矩形ABCD的顶点B在直线m上,则∠α=　　　　°.?

图5-1-3
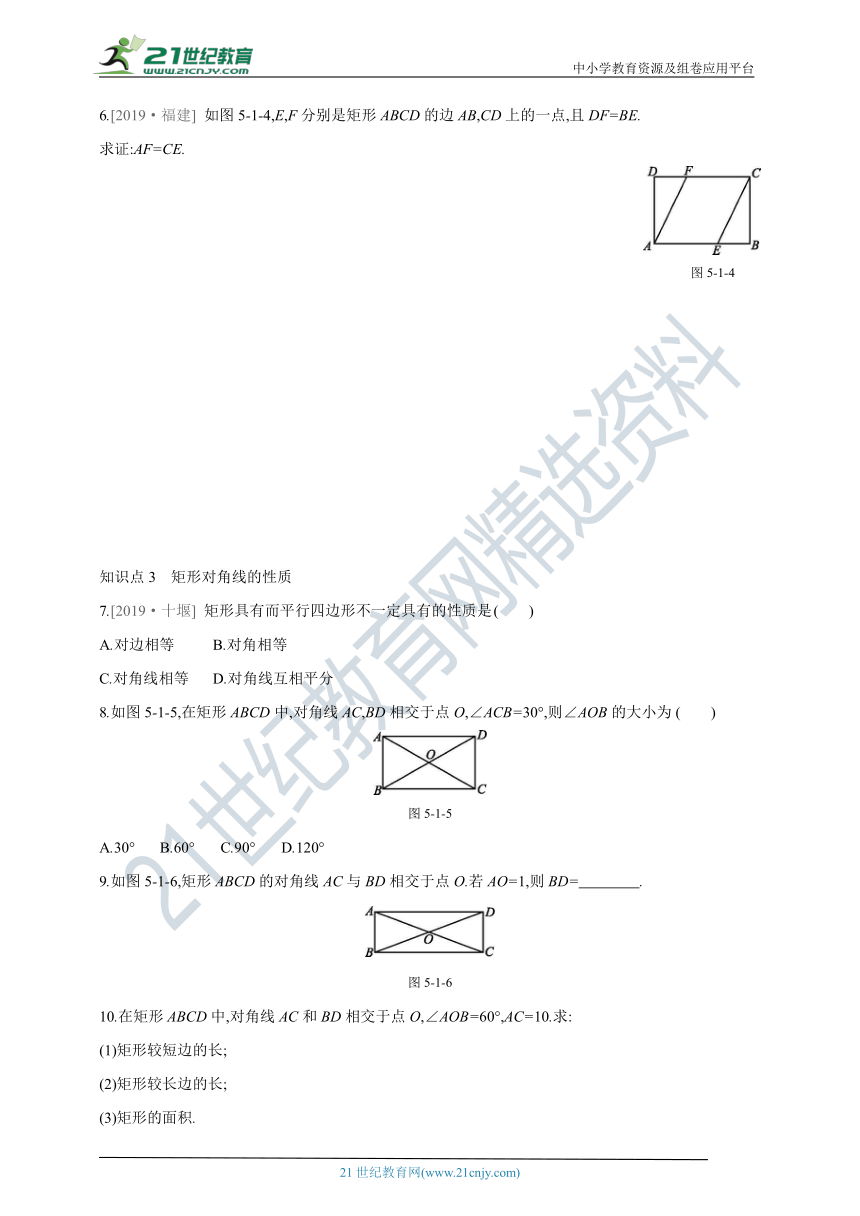
6.[2019·福建] 如图5-1-4,E,F分别是矩形ABCD的边AB,CD上的一点,且DF=BE.
求证:AF=CE.

图5-1-4








知识点3　矩形对角线的性质
7.[2019·十堰] 矩形具有而平行四边形不一定具有的性质是 (　　)
A.对边相等 B.对角相等
C.对角线相等 D.对角线互相平分
8.如图5-1-5,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为 (　　)

图5-1-5
A.30° B.60° C.90° D.120°
9.如图5-1-6,矩形ABCD的对角线AC与BD相交于点O.若AO=1,则BD=　　　　.?

图5-1-6
10.在矩形ABCD中,对角线AC和BD相交于点O,∠AOB=60°,AC=10.求:
(1)矩形较短边的长;
(2)矩形较长边的长;
(3)矩形的面积.

图5-1-7





11.如图5-1-8,在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.
求证:BE=CF.

图5-1-8




12.如图5-1-9,在矩形ABCD中,AB=2,AD=1,点M在边CD上.若MA平分∠DMB,则DM的长是 (　　)

　图5-1-9
A. B.
C.- D.2-
13.[2019·广州] 如图5-1-10,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为 (　　)

图5-1-10
A.4 B.4 C.10 D.8
14.[2017·绍兴] 在探索“尺规三等分角”这个数学名题的过程中,曾利用了图5-1-11.该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是 (　　)

　图5-1-11
A.7° B.21° C.23° D.24°
15.[2018·嘉兴期末] 如图5-1-12,在矩形ABCD中,E,F分别为AB,AD的中点,若EF=5,则AC=　　　　.?

图5-1-12
16.[2018·张家界] 如图5-1-13,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的长.

图5-1-13



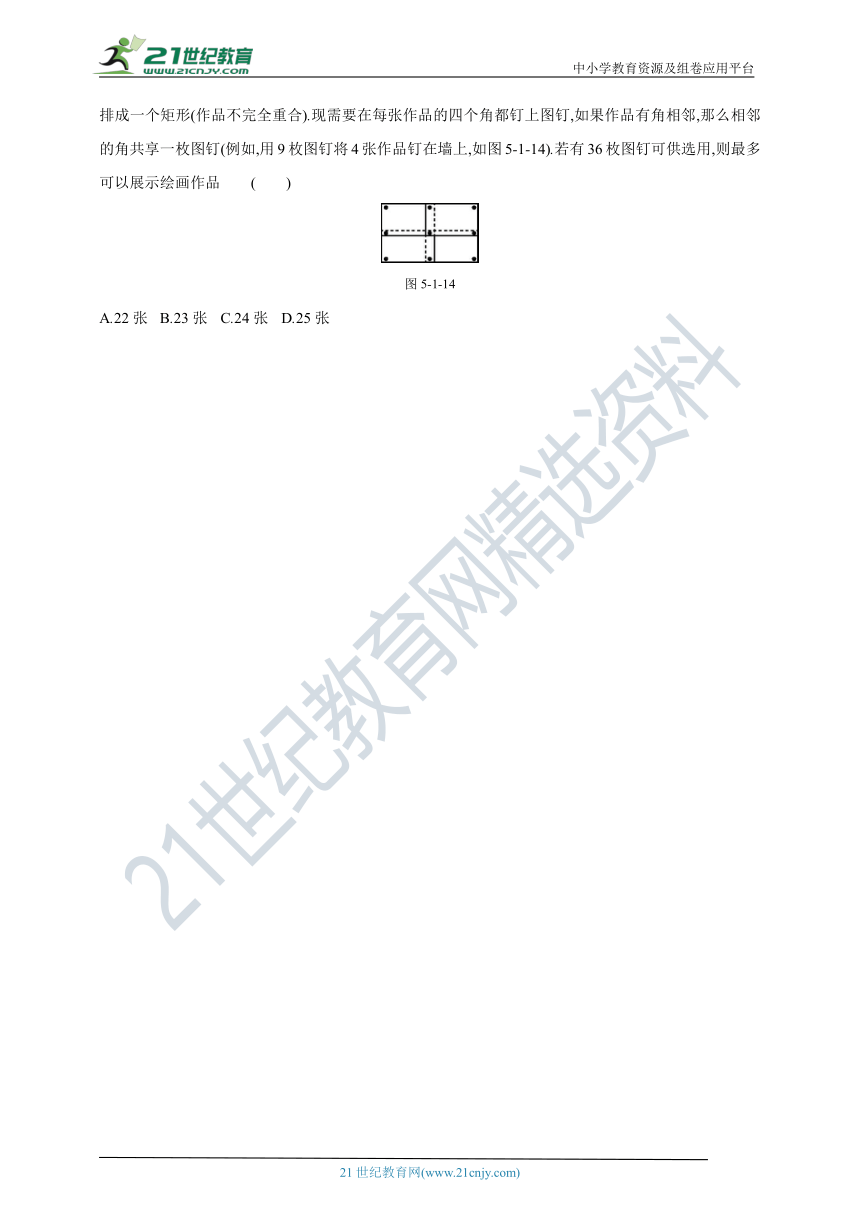
17.[2019·义乌模拟] 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角都钉上图钉,如果作品有角相邻,那么相邻的角共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图5-1-14).若有36枚图钉可供选用,则最多可以展示绘画作品 (　　)

图5-1-14
A.22张 B.23张 C.24张 D.25张




教师详解详析
1.证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∴∠ADB=90°.
又∵四边形ADBE是平行四边形,
∴平行四边形ADBE是矩形.
2.C　[解析] 因为矩形的每个角都是直角,所以两邻边和对角线构成直角三角形,所以BD==.
3.B　[解析] 在矩形ABCD中,A(1,1),B(3,1),C(3,5),∴CD∥x轴,AD∥BC∥y轴,∴点D的横坐标和点A的横坐标相同,都是1,点D的纵坐标和点C的纵坐标相同,都是5,即点D的坐标是(1,5).故选B.
4.A　[解析] 设AB=n,BC=m,
由题意得
解得
∵∠B=90°,
∴AC==10.
∵AP=PD=4,OA=OC=5,
∴OP=CD=3,
∴△AOP的周长为3+4+5=12.
故选A.
5.25
6.证明:∵四边形ABCD是矩形,
∴∠D=∠B=90°,AD=CB.
在△ADF和△CBE中,
∴△ADF≌△CBE(SAS),
∴AF=CE.
7.C
8.B
9.2　[解析] 在矩形ABCD中,
∵对角线AC与BD相交于点O,AO=1,
∴AO=CO=BO=DO=1,∴BD=2.
故答案为2.
10.解:(1)∵四边形ABCD是矩形,
∴OA=OB=OC.
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=AC=5,即矩形较短边的长为5.
(2)在Rt△ABC中,∠ABC=90°,AB=5,AC=10,则BC===5.
即矩形较长边的长是5.
(3)矩形的面积=AB·BC=5×5=25.
11.证明:∵四边形ABCD为矩形,
∴BO=CO.
∵BE⊥AC,CF⊥BD,
∴∠BEO=∠CFO=90°.
又∵∠BOE=∠COF,∴△BOE≌△COF,
∴BE=CF.
12.D　[解析] ∵四边形ABCD是矩形,
∴CD=AB=2,AB∥CD,BC=AD=1,∠C=90°,
∴∠BAM=∠AMD.
∵MA平分∠DMB,
∴∠AMD=∠AMB,
∴∠BAM=∠AMB,
∴BM=AB=2,
∴CM===,
∴DM=CD-CM=2-.
故选D.

13.A　[解析] 如图,连结AE.

∵EF是AC的垂直平分线,
∴OA=OC,AE=CE.
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE.
在△AOF和△COE中,
∴△AOF≌△COE(ASA),
∴AF=CE=5,
∴AE=CE=5,BC=BE+CE=3+5=8,
∴AB===4,
∴AC===4.
故选A.
14.C　[解析] ∵四边形ABCD是矩形,
∴∠D=90°,AB∥CD,AD∥BC,
∴∠FEA=∠ECD,∠DAC=∠ACB=21°.
∵∠ACF=∠AFC,∠FAE=∠FEA,
∴∠ACF=2∠FEA.
设∠ECD=x,则∠ACF=2x,
∴∠ACD=3x.
在Rt△ACD中,3x+21°=90°,
解得x=23°.故选C.
15.10　[解析] 连结BD,根据三角形中位线性质,可知BD=2EF=10,而矩形对角线AC=BD,所以AC=10.

16.解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠AEB=∠DAF.
又∵DF⊥AE,∴∠DFA=90°,
∴∠DFA=∠B.
又∵AD=EA,
∴△ADF≌△EAB,∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,∴AD=2DF.
∵DF=AB,∴AD=2AB=8.
17.D　[解析] ①如果所有的画展示成一行,36÷(1+1)-1=17(张),
∴36枚图钉最多可以展示17张画;
②如果所有的画展示成两行,36÷(2+1)-1=11(列),
2×11=22(张),
∴36枚图钉最多可以展示22张画;
③如果所有的画展示成三行,36÷(3+1)-1=8(列),
3×8=24(张),
∴36枚图钉最多可以展示24张画;
④如果所有的画展示成四行,36÷(4+1)=7(列)……1(枚),
4×6=24(张),
∴36枚图钉最多可以展示24张画;
⑤如果所有的画展示成五行,36÷(5+1)-1=5(列),
5×5=25(张),
∴36枚图钉最多可以展示25张画;
⑥如果所有的画展示成六行,36÷(6+1)=5(列)……1(枚),
6×4=24(张),
∴36枚图钉最多可以展示24张画;
⑦如果所有的画展示成七行,36÷(7+1)=4(列)……4(枚),
4-1=3(列),7×3+3=24(张),
∴36枚图钉最多可以展示24张画;…
依次类推,将所有的画展示成不同行,发现展示成五行时,可展示的画最多.
综上所述,36枚图钉最多可以展示25张画.
故选D.

















































21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)