5.3.2 正方形的性质同步练习(含答案)
文档属性
| 名称 | 5.3.2 正方形的性质同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 10:26:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.3 正方形
第2课时 正方形的性质
知识点1 正方形的性质
1.如图5-3-10,已知正方形ABCD的两条对角线相交于点O,那么此图中等腰直角三角形有 ( )
图5-3-10
A.4个 B.6个
C.8个 D.10个
2.若正方形的一条对角线的长为4,则这个正方形的面积是 ( )
A.8 B.4 C.8 D.16
3.如图5-3-11,正方形ABCD中,P,Q分别为BC,CD的中点,连结PQ,则∠CPQ的大小为( )
图5-3-11
A.50° B.60° C.45° D.70°
4.如图5-3-12,已知正方形ABCD,点E在边DC上,DE=3,EC=1,则AE的长为 .?
图5-3-12
5.[2019·台州天台县一模] 如图5-3-13,先将边长为6 cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',当两个三角形重叠部分的面积为8 cm2时,它移动的距离AA'等于 cm.?
图5-3-13
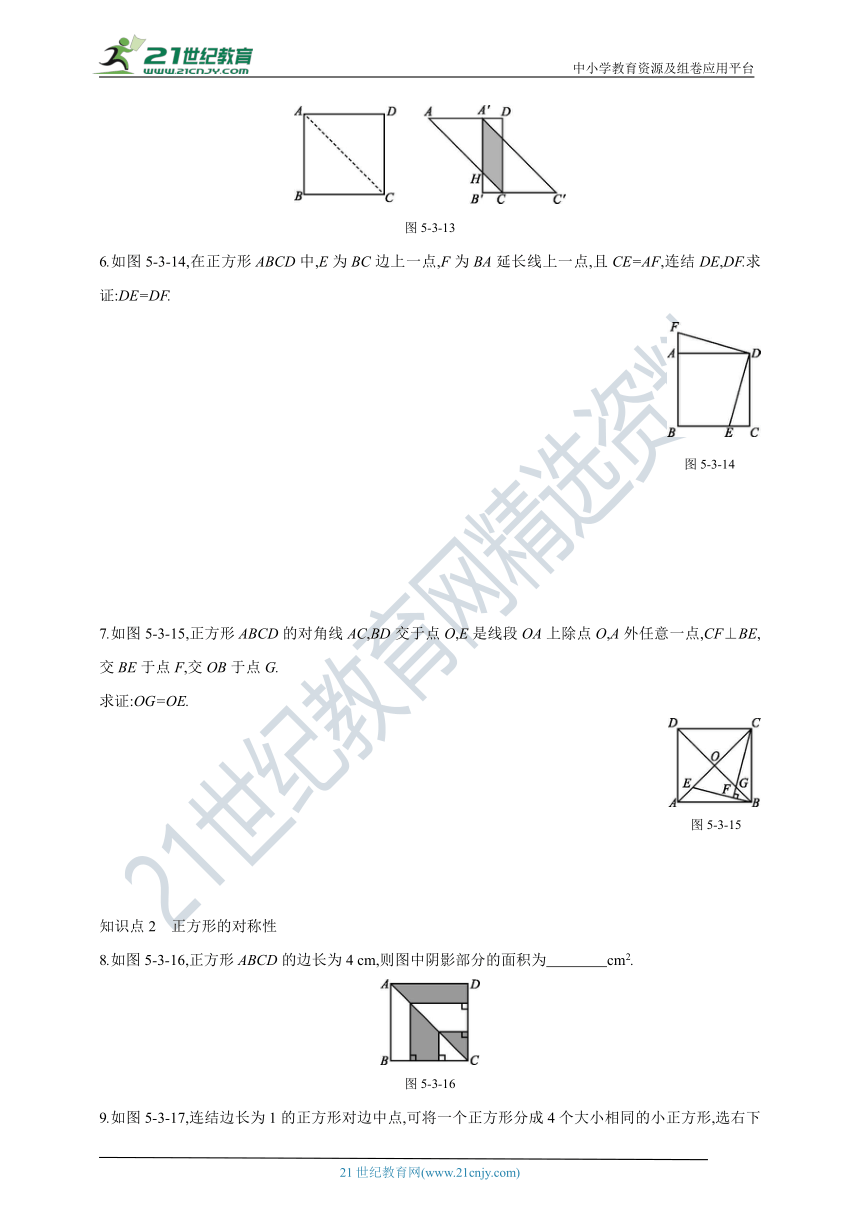
6.如图5-3-14,在正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连结DE,DF.求证:DE=DF.
图5-3-14
7.如图5-3-15,正方形ABCD的对角线AC,BD交于点O,E是线段OA上除点O,A外任意一点,CF⊥BE,交BE于点F,交OB于点G.
求证:OG=OE.
图5-3-15
知识点2 正方形的对称性
8.如图5-3-16,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 cm2.?
图5-3-16
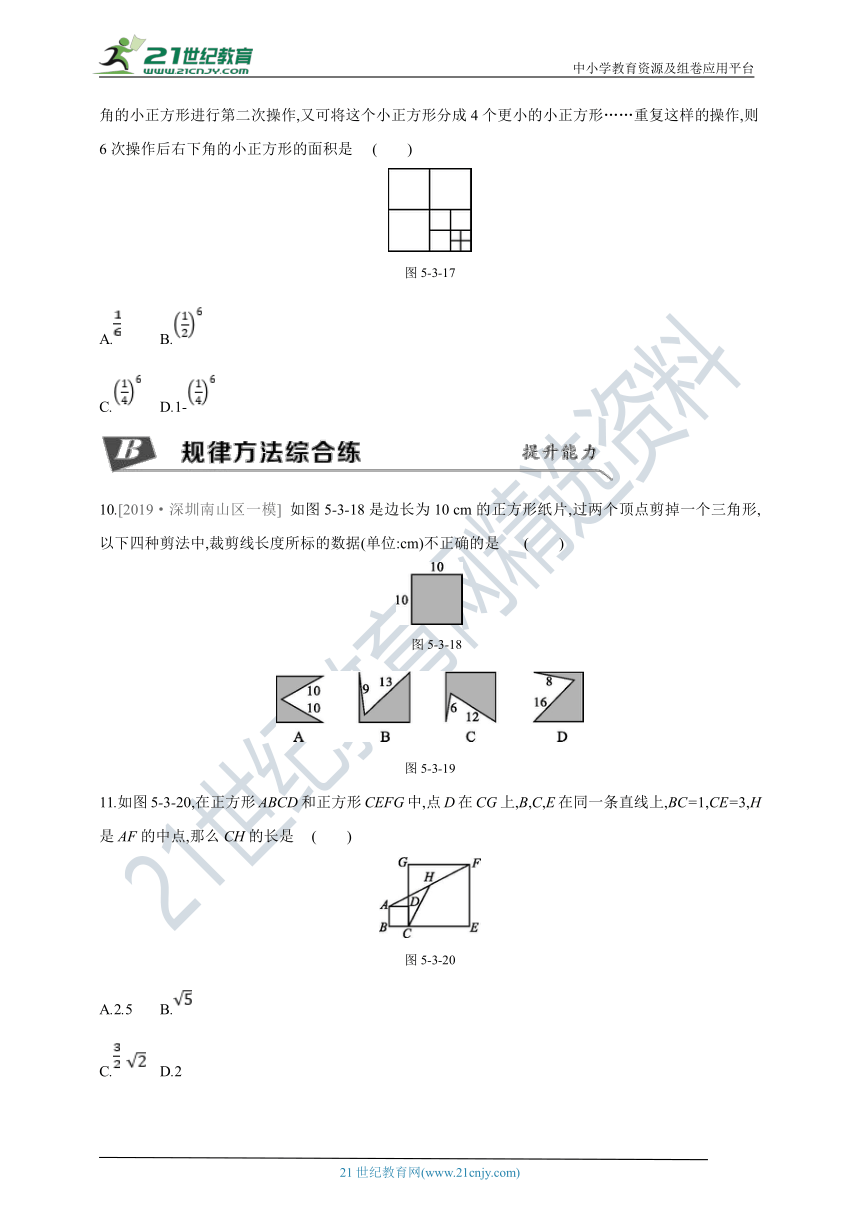
9.如图5-3-17,连结边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形……重复这样的操作,则6次操作后右下角的小正方形的面积是 ( )
图5-3-17
A. B.
C. D.1-
10.[2019·深圳南山区一模] 如图5-3-18是边长为10 cm的正方形纸片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是 ( )
图5-3-18
图5-3-19
11.如图5-3-20,在正方形ABCD和正方形CEFG中,点D在CG上,B,C,E在同一条直线上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
图5-3-20
A.2.5 B.
C. D.2
12.如图5-3-21,在正方形ABCD中,对角线AC与BD相交于点O,E是BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .?
图5-3-21
13.如图5-3-22,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .?
图5-3-22
14.[2018·遵义] 如图5-3-23,正方形ABCD的对角线交于点O,点E,F分别在AB,BC上(AE
(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.
图5-3-23
15.如图5-3-24,已知正方形ABCD和正方形CEFG的边长分别为10 cm和5 cm,点B,C,E在同一条直线上,点G在CD上.
(1)△BFD的面积为 cm2.?
(2)若将正方形CEFG的边长改为8 cm,则△BFD的面积为多少平方厘米?
(3)若去掉“正方形CEFG的边长为5 cm”这个条件,你还能求出△BFD的面积吗?若能,请求出;若不能,说明理由.
图5-3-24
详解详析
1.C [解析] ∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠BAD=90°,OA=OB=OC=OD,AC⊥BD,
∴△ABC,△ADC,△ABD,△BCD,△AOB,△BOC,△AOD,△COD都是等腰直角三角形.
故选C.
2.A [解析] ∵正方形的一条对角线长为4,
∴这个正方形的面积=×4×4=8.
故选A.
3.C [解析] ∵四边形ABCD为正方形,
∴BC=CD,∠BCD=90°.
∵P,Q分别为BC,CD的中点,
∴CP=CQ,
∴∠CPQ=45°.故选C.
4.5 [解析] ∵四边形ABCD是正方形,
∴AD=DC,∠D=90°.
∵DE=3,EC=1,∴AD=DC=4.
在Rt△ADE中,AE===5.
5.2或4 [解析] 令AA'=x.
由图可知:A'D=6-x,A'H=x,
∴S阴=A'H·A'D=x·(6-x)=8,
解得x=2或4,
∴AA'=2或4.
6.证明:在正方形ABCD中,AD=CD,∠DAB=∠C=90°,
∴∠DAF=90°=∠C.
在△DCE和△DAF中,
∴△DCE≌△DAF,∴DE=DF.
7.证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OB=OC,OC⊥OB,
∴∠COG=∠BOE=90°.
∵CF⊥BE,
∴∠CEB+∠ECF=90°.
∵∠CEB+∠OBE=90°,
∴∠OCG=∠OBE,
∴△OCG≌△OBE(ASA),
∴OG=OE.
8.8
9.C
10.D [解析] 选项D不正确.理由:
∵正方形的边长为10,
∴对角线长=10≈14.
∵16>14,
∴这个图形不可能存在.
故选D.
11.B
12.3.5 [解析] ∵CE=5,△CEF的周长为18,
∴CF+EF=18-5=13.
∵F为DE的中点,∴DF=EF.
∵∠BCD=90°,
∴CF=DE=DF,
∴CF+EF=DF+EF=DE=13,
∴CD===12.
∵四边形ABCD是正方形,
∴BC=CD=12,O为BD的中点,
∴OF是△BDE的中位线,
∴OF=BE=(BC-CE)=×(12-5)=3.5.
13. [解析] 因为正方形ABCD的边长为4,BE=1,AF=2,在AD上截取AM=2,连结EM,则EM的长为PF+PE的最小值,过点M作MN⊥BC于点N,由题意可知EN=BN-BE=AM-BE=AF-BE=2-1=1,MN=4,所以EM===.
14.解:(1)证明:正方形ABCD中,∵AC=BD,OA=AC,OB=OD=BD,
∴OA=OB=OD.
∵AC⊥BD,∴∠AOB=∠AOD=90°,
∴∠OAD=∠OBA=45°,
∴∠OAM=∠OBN.
又∵∠EOF=90°,
∠AOM+∠MOB=90°,∠BON+∠MOB=90°,
∴∠AOM=∠BON,
∴△AOM≌△BON,∴OM=ON.
(2)如图,过点O作OP⊥AB于点P,则∠OPA=90°,
∴∠OPA=∠MAE.
∵E为OM的中点,
∴OE=ME.
又∵∠AEM=∠PEO,
∴△AEM≌△PEO,
∴AE=PE.
∵OA=OB,OP⊥AB,
∴AP=BP=AB=2,
∴PE=1.
在Rt△OPB中,∵∠OBP=45°,
∴OP=BP=2.
在Rt△OEP中,∵OE==,
∴OM=2OE=2.
在Rt△OMN中,∵OM=ON,
∴MN=OM=2.
15.解:(1)50
(2)延长EF,AD交于点M,则四边形ABEM为矩形.
S△BFD=S矩形ABEM-S△BEF-S△MDF-S△ABD=(10+8)×10-×(10+8)×8-×(10-8)×8-×10×10=50(cm2).
(3)能,△BFD的面积仍为50 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
