第四章 平行四边形中的面积问题复习课件(共26张PPT)
文档属性
| 名称 | 第四章 平行四边形中的面积问题复习课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 609.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 09:47:18 | ||
图片预览


文档简介
(共26张PPT)
平行四边形中的面积问题
初 中 数 学 专 题 讲 练
一、利用平行线解题
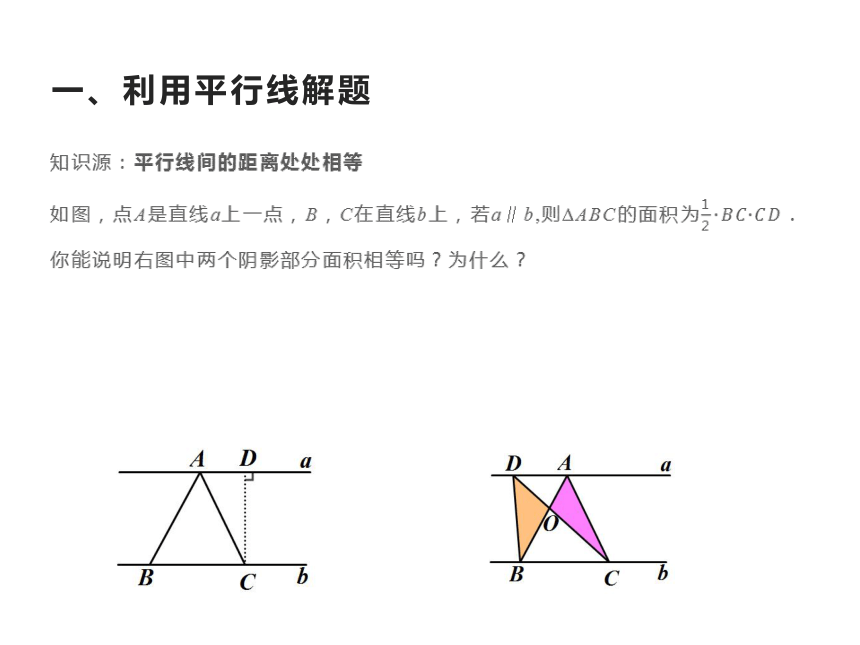
知识源:平行线间的距离处处相等
如图,点A是直线a上一点,B,C在直线b上,若a∥b,则 ABC的面积为
你能说明右图中两个阴影部分面积相等吗?为什么?
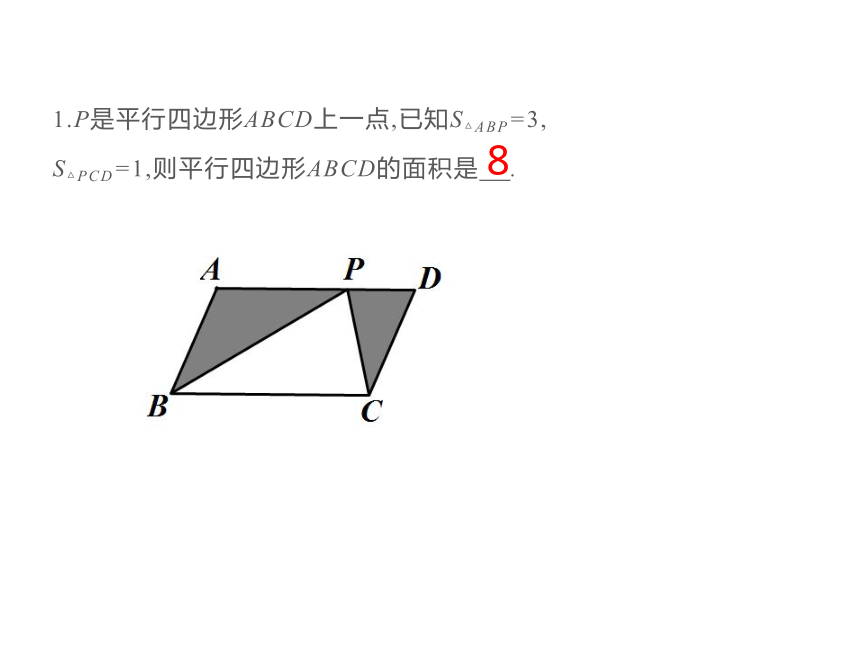
1.P是平行四边形ABCD上一点,已知S△ABP=3,
S△PCD=1,则平行四边形ABCD的面积是 .
8
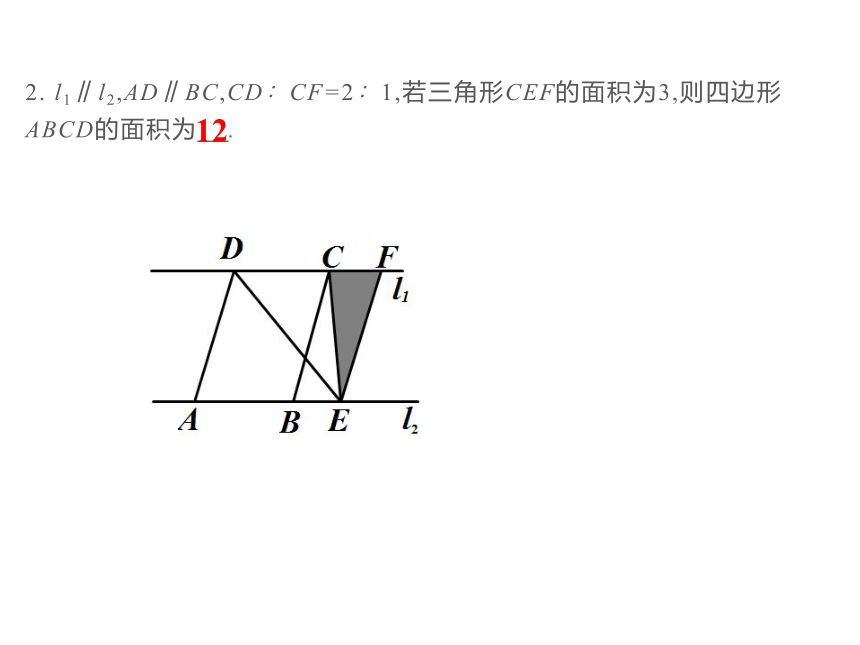
2. l1∥l2,AD∥BC,CD∶CF=2∶1,若三角形CEF的面积为3,则四边形ABCD的面积为 .
12
3. 在□ABCD中,AB=4,BC=6,∠ABC,∠ADC的平分线分别交AD,BC于点E,F.若□ ABCD的面积为18,则四边形BFDE的面积为______
6
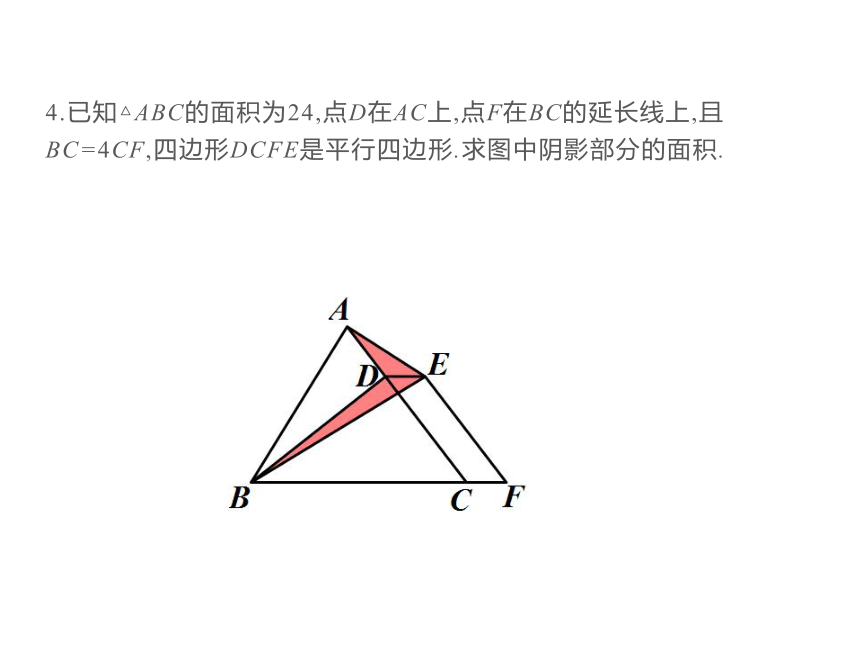
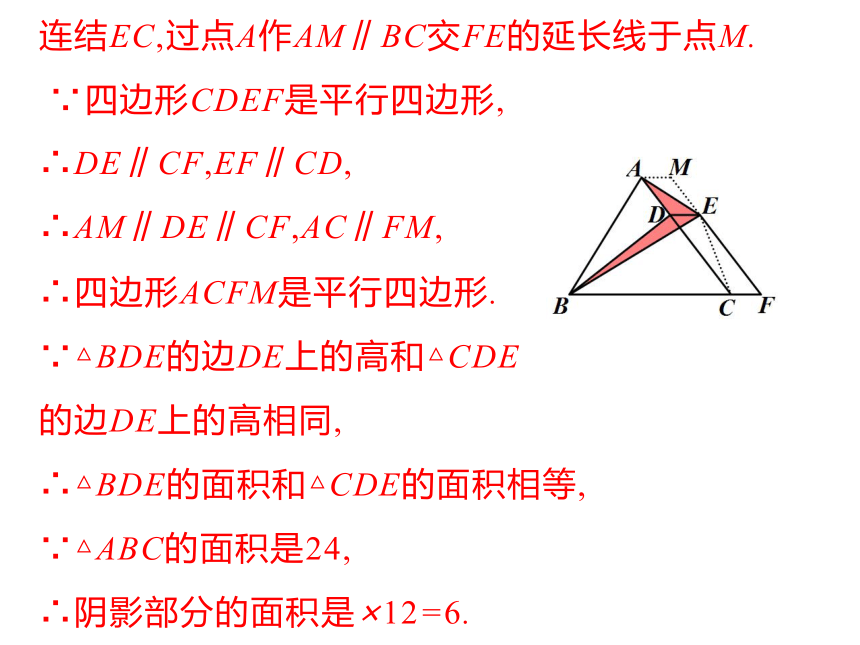
4.已知△ABC的面积为24,点D在AC上,点F在BC的延长线上,且BC=4CF,四边形DCFE是平行四边形.求图中阴影部分的面积.
连结EC,过点A作AM∥BC交FE的延长线于点M.
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形.
∵△BDE的边DE上的高和△CDE
的边DE上的高相同,
∴△BDE的面积和△CDE的面积相等,
∵△ABC的面积是24,
∴阴影部分的面积是×12=6.
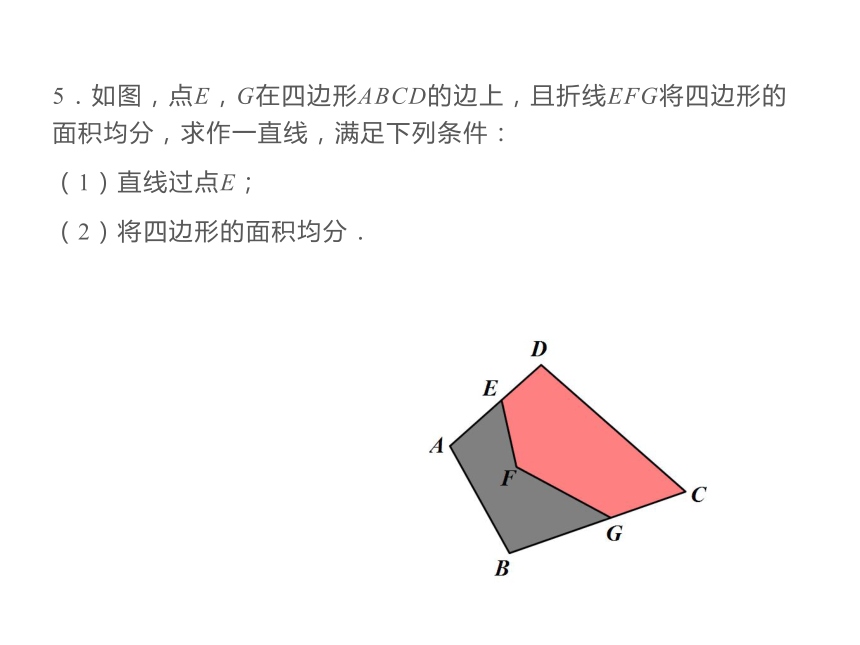
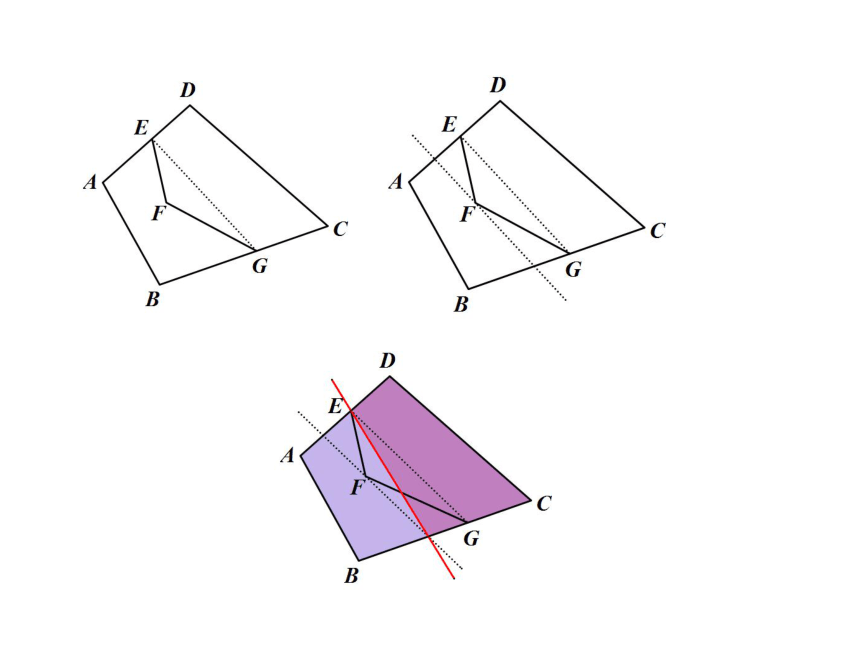
5.如图,点E,G在四边形ABCD的边上,且折线EFG将四边形的面积均分,求作一直线,满足下列条件:
(1)直线过点E;
(2)将四边形的面积均分.
6.如图,在四边形ABCD中,画一直线,将四边形的面积均分.
二、利用中心对称解题
知识源:平行四边形是中心对称图形,经过对称中心的直线等分面积.
如图,四边形ABCD是平行四边形,点O是对称中心,所有经过点O的直线都能将四边形的面积均分.
1.如图,点E,F在□ABCD的对边上,若□ABCD的面积是40 cm2,则阴影部分的面积是 .
20
2. (1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”或“=”);
(2)两个正方形如图②所示摆放,O为小正方形对角线的交点,作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,作直线将整个图形分成面积相等的两部分(用三种方法分割).
3.如图,在矩形ABCD形状的木板中有一个圆形的洞,请画一条锯痕,将剩余木板的面积均分.
三、利用中线或中位线解题
知识源:
1.三角形的中线将三角形的面积均分;
2.三角形的中位线将三角形面积分成1:3两部分.
1.O是 ABCD的对角线交点,E为AB的中点,若S ABCD=16,则S△DOE的值为___.
2
2.如图,E,F,G,H分别是四边形ABCD的中点,若四边形ABCD的面积为100,求四边形EFGH的面积.
如图,连接BD,则S ABD=4S AEH,同理: S CBD=4S CFG
∴四边形ABCD的面积=4(S AEH+ S CFG ),即S AEH+ S CFG =25,同理: S BEF+ S DHG =25
∴四边形EFGH的面积为四边形ABCD面积的一半,即50
3.在□ABCD中,A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD的五等分点,B1,B2和D1,D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为1,求平行四边形ABCD的面积.
将每个小格的面积设为k,根据等分点可知:
S ABCD=15k,而四边形A4B2C4D2的面积=15k-k-2k-2k-k=9k=1,∴
∴四边形ABCD的面积为
如图,一个四边形形状的池塘ABCD的四个顶点处各有一棵桃树,现欲将池塘扩建,要求如下:
(1)保留桃树的原位置不变;
(2)扩建后的池塘形状是平行四边形;
(3)扩建后池塘的面积为原池塘面积的2倍.
请画出示意图.
如图:
平行四边形中的面积问题
初 中 数 学 专 题 讲 练
一、利用平行线解题
知识源:平行线间的距离处处相等
如图,点A是直线a上一点,B,C在直线b上,若a∥b,则 ABC的面积为
你能说明右图中两个阴影部分面积相等吗?为什么?
1.P是平行四边形ABCD上一点,已知S△ABP=3,
S△PCD=1,则平行四边形ABCD的面积是 .
8
2. l1∥l2,AD∥BC,CD∶CF=2∶1,若三角形CEF的面积为3,则四边形ABCD的面积为 .
12
3. 在□ABCD中,AB=4,BC=6,∠ABC,∠ADC的平分线分别交AD,BC于点E,F.若□ ABCD的面积为18,则四边形BFDE的面积为______
6
4.已知△ABC的面积为24,点D在AC上,点F在BC的延长线上,且BC=4CF,四边形DCFE是平行四边形.求图中阴影部分的面积.
连结EC,过点A作AM∥BC交FE的延长线于点M.
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形.
∵△BDE的边DE上的高和△CDE
的边DE上的高相同,
∴△BDE的面积和△CDE的面积相等,
∵△ABC的面积是24,
∴阴影部分的面积是×12=6.
5.如图,点E,G在四边形ABCD的边上,且折线EFG将四边形的面积均分,求作一直线,满足下列条件:
(1)直线过点E;
(2)将四边形的面积均分.
6.如图,在四边形ABCD中,画一直线,将四边形的面积均分.
二、利用中心对称解题
知识源:平行四边形是中心对称图形,经过对称中心的直线等分面积.
如图,四边形ABCD是平行四边形,点O是对称中心,所有经过点O的直线都能将四边形的面积均分.
1.如图,点E,F在□ABCD的对边上,若□ABCD的面积是40 cm2,则阴影部分的面积是 .
20
2. (1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”或“=”);
(2)两个正方形如图②所示摆放,O为小正方形对角线的交点,作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,作直线将整个图形分成面积相等的两部分(用三种方法分割).
3.如图,在矩形ABCD形状的木板中有一个圆形的洞,请画一条锯痕,将剩余木板的面积均分.
三、利用中线或中位线解题
知识源:
1.三角形的中线将三角形的面积均分;
2.三角形的中位线将三角形面积分成1:3两部分.
1.O是 ABCD的对角线交点,E为AB的中点,若S ABCD=16,则S△DOE的值为___.
2
2.如图,E,F,G,H分别是四边形ABCD的中点,若四边形ABCD的面积为100,求四边形EFGH的面积.
如图,连接BD,则S ABD=4S AEH,同理: S CBD=4S CFG
∴四边形ABCD的面积=4(S AEH+ S CFG ),即S AEH+ S CFG =25,同理: S BEF+ S DHG =25
∴四边形EFGH的面积为四边形ABCD面积的一半,即50
3.在□ABCD中,A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD的五等分点,B1,B2和D1,D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为1,求平行四边形ABCD的面积.
将每个小格的面积设为k,根据等分点可知:
S ABCD=15k,而四边形A4B2C4D2的面积=15k-k-2k-2k-k=9k=1,∴
∴四边形ABCD的面积为
如图,一个四边形形状的池塘ABCD的四个顶点处各有一棵桃树,现欲将池塘扩建,要求如下:
(1)保留桃树的原位置不变;
(2)扩建后的池塘形状是平行四边形;
(3)扩建后池塘的面积为原池塘面积的2倍.
请画出示意图.
如图:
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
