浙教版九年级下册数学第2章 一元二次方程 复习 课件(1)(共25张PPT)
文档属性
| 名称 | 浙教版九年级下册数学第2章 一元二次方程 复习 课件(1)(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:51:56 | ||
图片预览







文档简介
(共25张PPT)
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
方程两边都是整式
ax?+bx+c=0(a?0)
只含有一个未知数
求知数的最高次数是2
配 方 法
求 根 公式法
直接开平方法
因 式 分解法
二次项系数为1,而一次项系数为偶数
判断下列方程是不是一元二次方程,若不是一元二次方程,请说明理由?
1、(x-1)2=4
2、x2-2x=8
4、x2=y+1
5、x3-2x2=1
6、ax2 + bx + c=1
×
√
√
×
×
×
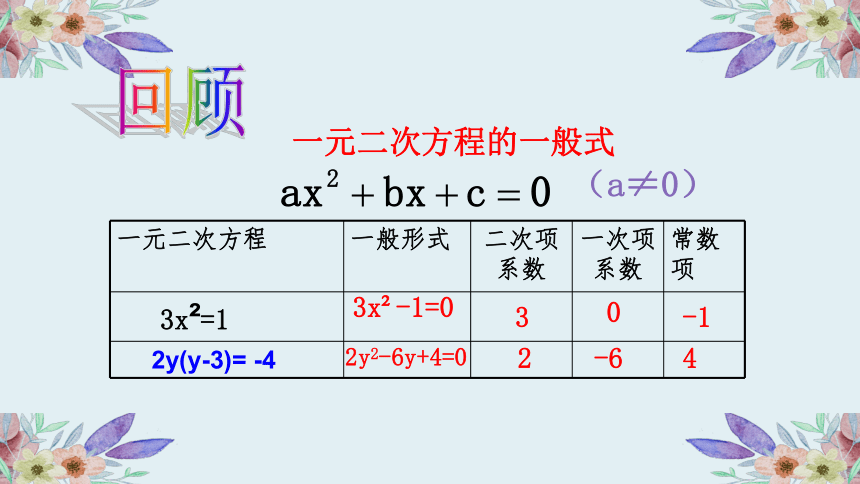
一元二次方程的一般式
(a≠0)
3x?-1=0
3
2
-6
-1
4
0
2y2-6y+4=0
一元二次方程 一般形式 二次项系数 一次项系数 常数项
3x?=1
2y(y-3)= -4
2
3.若x=2是方程x2+ax-8=0的解,则a= ;
2
4、写出一个根为2,另一个根为5的一元二次方程 。
≠- 2
2、已知一元二次方程x2=2x 的解是( )
(A)0 (B)2 (C)0或-2 (D)0或2
D
1、已知一元二次方程(x+1)(2x-1)=0的解是( )
(A)-1 (B)1/2 (C)-1或-2 (D)-1或1/2
D
用适当的方法解下列方程
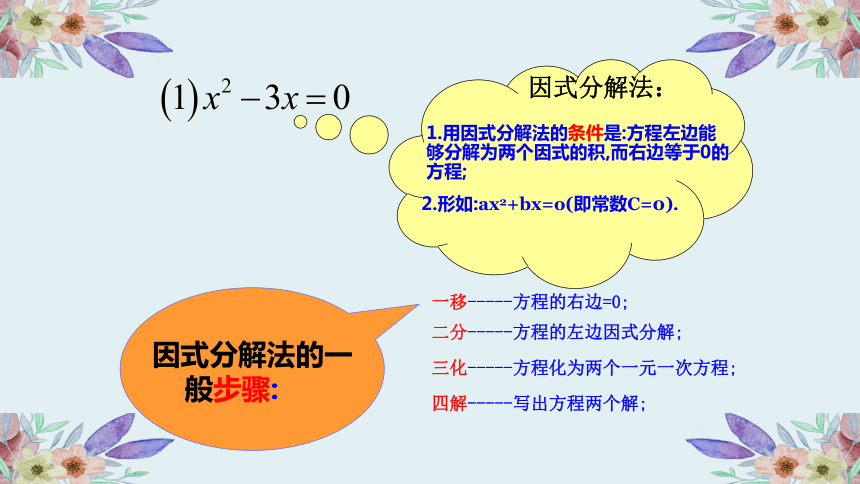
因式分解法:
1.用因式分解法的条件是:方程左边能够分解为两个因式的积,而右边等于0的方程;
2.形如:ax2+bx=o(即常数C=0).
因式分解法的一般步骤:
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
直接开平方法:
1.用开平方法的条件是:缺少一次项的一元二次方程,用开平方法比较方便;
2.形如:ax2+c=o (即没有一次项).
a(x+m)2=k
配方法:
用配方法的条件是:适应于任何一个一元二次方程,但是在没有特别要求的情况下,除了形如x2+2kx+c=0 用配方法外,一般不用;(即二次项系数为1,一次项系数是偶数。)
配方法的一般步骤:
一除----把二次项系数化为1(方程的两边同
时除以二次项系数a)
二移----把常数项移到方程的右边;
三配----把方程的左边配成一个完全平方式;
四开----利用开平方法求出原方程的两个解.
★一除、二移、三配、四开、五解.
公式法:
用公式法的条件是:适应于任何一个一元二次方程,先将方程化为一般形式,再求出b2-4ac的值, b2-4ac≥0则方程有实数根, b2-4ac<0则方程无实数根;
方程根的情况与b2-4ac的值的关系:
当b2-4ac>0 时,方程有两个不相等的实数根;
当b2-4ac=0 时,方程有两个相等的实数根;
当b2-4ac<0 时,方程没有实数根.
公式法虽然是万能的,对任何一元二次方程都适用,但不一定是最简单的,因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法,若不行,再考虑公式法(适当也可考虑配方法)
选择适当的方法解下列方程
你说我说大家说:
通过今天的学习你有什么收获或感受?
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
方程两边都是整式
ax?+bx+c=0(a?0)
只含有一个未知数
求知数的最高次数是2
配 方 法
求 根 公式法
直接开平方法
因 式 分解法
二次项系数为1,而一次项系数为偶数
已知方程x2+kx = - 3? 的一个根是-1,则k= , 另一根为______
4
x=-3
6
构造一个一元二次方程,要求:
(1)常数项为零(2)有一根为2。
解方程:
解方程:
m取什么值时,方程 x2+(2m+1)x+m2-4=0有两个相等的实数解
说明:当二次项系数也含有待定的字母时,要注意二次项系数不能为0,还要注意题目中待定字母的取值范围.
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
方程两边都是整式
ax?+bx+c=0(a?0)
只含有一个未知数
求知数的最高次数是2
配 方 法
求 根 公式法
直接开平方法
因 式 分解法
二次项系数为1,而一次项系数为偶数
判断下列方程是不是一元二次方程,若不是一元二次方程,请说明理由?
1、(x-1)2=4
2、x2-2x=8
4、x2=y+1
5、x3-2x2=1
6、ax2 + bx + c=1
×
√
√
×
×
×
一元二次方程的一般式
(a≠0)
3x?-1=0
3
2
-6
-1
4
0
2y2-6y+4=0
一元二次方程 一般形式 二次项系数 一次项系数 常数项
3x?=1
2y(y-3)= -4
2
3.若x=2是方程x2+ax-8=0的解,则a= ;
2
4、写出一个根为2,另一个根为5的一元二次方程 。
≠- 2
2、已知一元二次方程x2=2x 的解是( )
(A)0 (B)2 (C)0或-2 (D)0或2
D
1、已知一元二次方程(x+1)(2x-1)=0的解是( )
(A)-1 (B)1/2 (C)-1或-2 (D)-1或1/2
D
用适当的方法解下列方程
因式分解法:
1.用因式分解法的条件是:方程左边能够分解为两个因式的积,而右边等于0的方程;
2.形如:ax2+bx=o(即常数C=0).
因式分解法的一般步骤:
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
直接开平方法:
1.用开平方法的条件是:缺少一次项的一元二次方程,用开平方法比较方便;
2.形如:ax2+c=o (即没有一次项).
a(x+m)2=k
配方法:
用配方法的条件是:适应于任何一个一元二次方程,但是在没有特别要求的情况下,除了形如x2+2kx+c=0 用配方法外,一般不用;(即二次项系数为1,一次项系数是偶数。)
配方法的一般步骤:
一除----把二次项系数化为1(方程的两边同
时除以二次项系数a)
二移----把常数项移到方程的右边;
三配----把方程的左边配成一个完全平方式;
四开----利用开平方法求出原方程的两个解.
★一除、二移、三配、四开、五解.
公式法:
用公式法的条件是:适应于任何一个一元二次方程,先将方程化为一般形式,再求出b2-4ac的值, b2-4ac≥0则方程有实数根, b2-4ac<0则方程无实数根;
方程根的情况与b2-4ac的值的关系:
当b2-4ac>0 时,方程有两个不相等的实数根;
当b2-4ac=0 时,方程有两个相等的实数根;
当b2-4ac<0 时,方程没有实数根.
公式法虽然是万能的,对任何一元二次方程都适用,但不一定是最简单的,因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法,若不行,再考虑公式法(适当也可考虑配方法)
选择适当的方法解下列方程
你说我说大家说:
通过今天的学习你有什么收获或感受?
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
方程两边都是整式
ax?+bx+c=0(a?0)
只含有一个未知数
求知数的最高次数是2
配 方 法
求 根 公式法
直接开平方法
因 式 分解法
二次项系数为1,而一次项系数为偶数
已知方程x2+kx = - 3? 的一个根是-1,则k= , 另一根为______
4
x=-3
6
构造一个一元二次方程,要求:
(1)常数项为零(2)有一根为2。
解方程:
解方程:
m取什么值时,方程 x2+(2m+1)x+m2-4=0有两个相等的实数解
说明:当二次项系数也含有待定的字母时,要注意二次项系数不能为0,还要注意题目中待定字母的取值范围.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
