2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第1课时课件(37张ppt)
文档属性
| 名称 | 2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第1课时课件(37张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 919.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 11:13:56 | ||
图片预览









文档简介
课件34张PPT。第1课时 1.二次函数y=ax2+k的图象
(1)通过在同一坐标系中画函数 与 的图象,可以
得到:它们的对称轴都是__轴(直线____);开口方向都是开口
_____;顶点不同,函数 的顶点坐标为______,
的顶点坐标为______.yx=0向上(0,0)(0,1)(2)通过观察二次函数 与 的图象还可以得到:
当自变量x取同一数值时,函数 的函数值都比 的
函数值____,从图象位置上看,函数 的图象上每一点都
在函数 的图象上相应点的上方_____单位.函数
的图象可以看成是将函数 的图象向___平移___个单位得
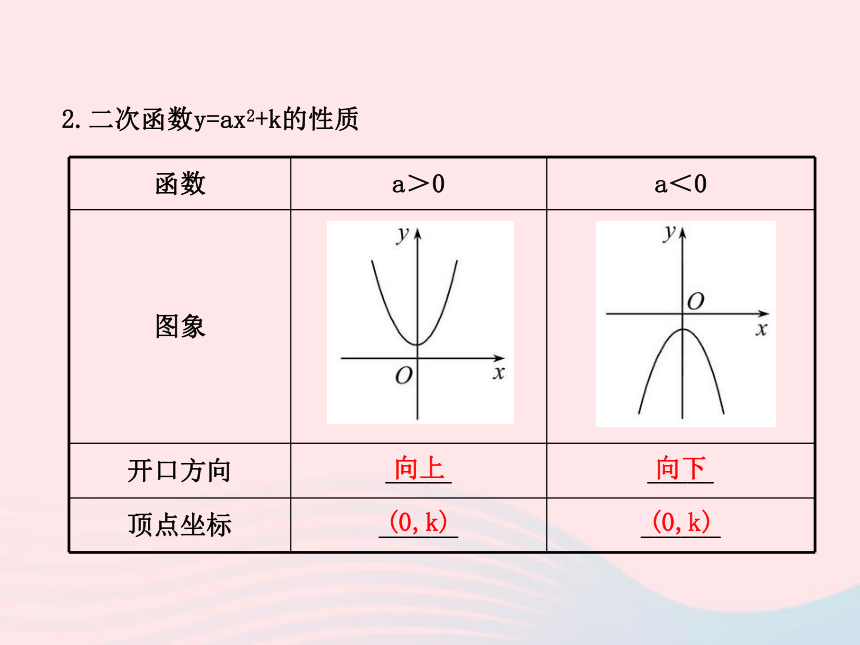
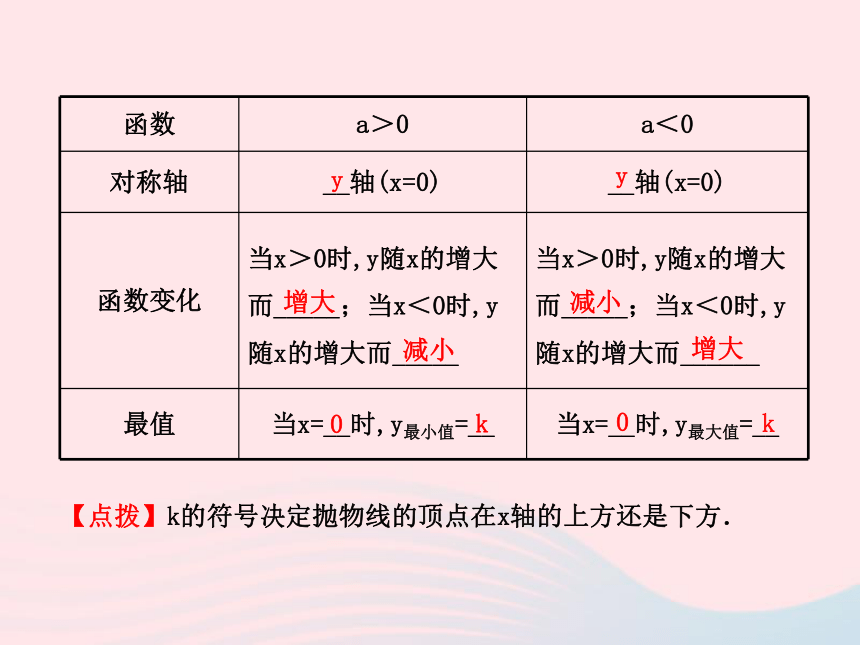
到的. 大1一个上一2.二次函数y=ax2+k的性质 向上向下(0,k)(0,k)增大减小减小增大0k0k【点拨】k的符号决定抛物线的顶点在x轴的上方还是下方. yy【预习思考】函数y=x2与y=-x2+1的图象形状是否相同?
提示:它们的形状相同,只是开口方向不同,顶点坐标也不相
同. 二次函数y=ax2+k的图象与性质
【例1】已知下列函数.
y=3x2;y=3x2+2;y=-3x2;y=3x2-2.
(1)指出以上四个二次函数的开口方向、对称轴、顶点坐标及最
值;
(2)函数y=3x2的图象分别与y=3x2+2,y=3x2-2的图象有怎样的联
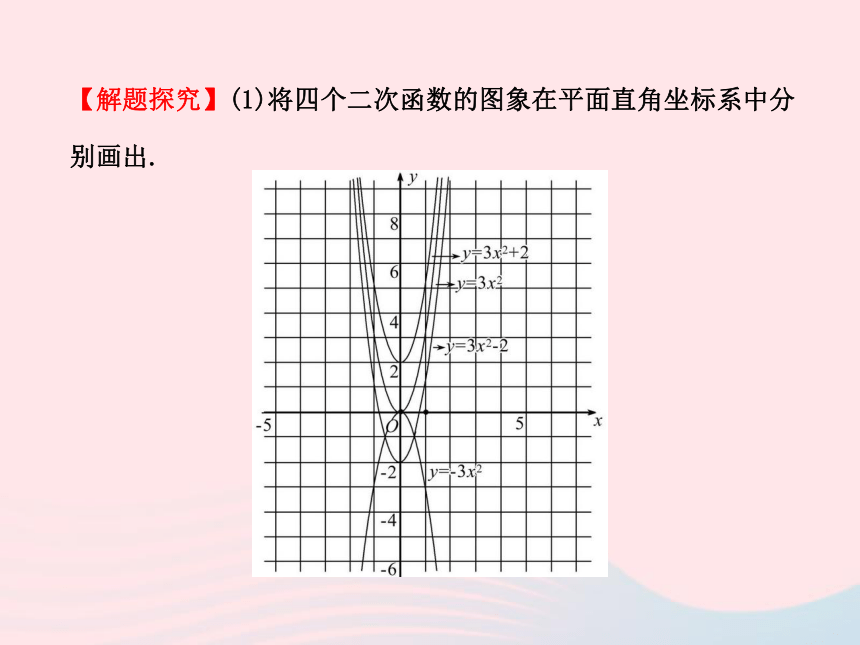
系?【解题探究】(1)将四个二次函数的图象在平面直角坐标系中分
别画出. 可得:①y=3x2,y=3x2+2与y=3x2-2的开口向上,y=-3x2的开口
向下.
②四个二次函数图象的对称轴均为y轴.
③y=3x2和y=-3x2的顶点坐标为(0,0).y=3x2+2的顶点坐标为
(0,2),y=3x2-2的顶点坐标为(0,-2).
④y=3x2,当x=0时,y最小值=0.
y=3x2+2,当x=0时,y最小值=2.
y=-3x2,当x=0时,y最大值=0.
y=3x2-2,当x=0时,y最小值=-2. (2)通过观察图象可得:
y=3x2+2的图象是将y=3x2的图象向上平移2个单位得到的,
y=3x2-2的图象是将y=3x2的图象向下平移2个单位得到的.【互动探究】函数y=3x2+2的图象经过怎样的平移可得到函数
y=3x2-2的图象?
提示:函数y=3x2+2的图象沿y轴向下平移4个单位可得到函数
y=3x2-2的图象.【规律总结】
函数y=ax2+k的性质口诀
a大于0,口向上,y轴左减右是增,x为0,k最小;
a小于0,口向下,y轴左增右是减,x为0,k最大. 【跟踪训练】
1.抛物线y=-2x2+1的对称轴是( )
(A)直线 (B)直线
(C)y轴 (D)直线x=2
【解析】选C.根据二次函数y=ax2+k的性质可知y=-2x2+1的对称
轴是y轴. 2.下列函数的图象在每一个象限内,y值随x值
的增大而增大的是( )
(A)y=-x+1 (B)y=x2-1
(C)y= (D)【解析】选D.A:对于一次函数y=-x+1,k<0,函数的图象在每一
个象限内,y值随x值的增大而减小,故本选项错误;B:对于二次
函数y=x2-1,当x>0时,y值随x值的增大而增大,当x<0时,y值随
x值的增大而减小,故本选项错误;C:对于反比例函数 ,
k>0,函数的图象在每一个象限内,y值随x值的增大而减小,故本
选项错误;D:对于反比例函数 ,k<0,函数的图象在每一
个象限内,y值随x值的增大而增大,故本选项正确.【变式训练】若二次函数 与y=-x2+k的图象的顶点重
合,则下列结论不正确的是( )
(A)这两个函数图象有相同的对称轴
(B)这两个函数图象的开口方向相反
(C)方程-x2+k=0没有实数根
(D)二次函数y=-x2+k的最大值为
【解析】选C.∵二次函数 与y=-x2+k的图象的顶点重
合,∴ ,∴A,B,D正确;当 时,方程-x2+k=0有实数
根,故C不正确. 3.将抛物线y=x2的图象向上平移1个单位,则
平移后的抛物线的关系式为____________.
【解析】∵图象向上(下)平移,横坐标不变,
∴由题意得,y=x2+1.
答案:y=x2+1 二次函数y=ax2+k的性质的应用
【例2】如图,小河上有一拱桥,拱桥
及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,
ED,DB组成,已知河底ED是水平的,ED=16 m,AE=8 m,抛物线
的顶点C到ED的距离是11 m,以ED所在的直线为x轴,抛物线的
对称轴为y轴建立平面直角坐标系. (1)求抛物线的函数关系式;
(2)已知从某时刻开始的40 h内,水面与河底ED的距离h(单位:m)
随时间t(单位:h)的变化满足函数关系h= (0≤
t≤40)且当水面到顶点C的距离不大于5 m时,需禁止船只通行,
请通过计算说明:在这一时段内,需多少小时禁止船只通行? 【规范解答】(1)设抛物线所对应的函数关系式为y=ax2+11,
由题意得B(8,8),…………………………………………2分
∴64a+11=8,解得a= ,………………………………3分
∴ .………………………………………4分(2)水面到顶点C的距离不大于5 m时,即水面与河底ED的距离h
至少为6m,
∴6= ,……………………………………5分
解得t1=35,t2=3,…………………………………………6分
∴需要35-3=32(h).
答:需32小时禁止船只通行.……………………………7分【规律总结】
利用y=ax2+k的图象及性质解决生活中实际问题的步骤
1.首先建立适当的坐标系.
2.根据图象上的点确定函数关系式.
3.利用抛物线的特点与性质解决具体问题.【跟踪训练】
4.赵州桥的桥拱是抛物线形,建立如
图所示的坐标系,其对应的函数关系
式为 ,当水位线在AB位置时,
水面宽AB=30米,这时水面离桥顶的高
度h是( )
(A)5米 (B)6米 (C)8米 (D)9米
【解析】选D.y= ,|-9|=9.5.隧道的截面是抛物线,且抛物线所对应的函数关系式为
,一辆车高3 m,宽4 m,该车______(填写“能”
或“不能”)通过隧道.
【解析】在 中,
当y=3时, ,解得:
x=± ,所以宽是 <4 m,即不能通过.
答案:不能6.如图,某大学校门是一抛物线形水泥建筑物,大门的地面宽度
为8 m,两侧距地面4 m高处各挂一个牌匾,且两牌匾顶部的水平
距离为6 m,则该大学校门的高度约是多少?(精确到 0.1,建筑厚
度不计)【解析】以校门所在地面线段的中点为原点建立平面直角坐标
系,如图,设抛物线所对应的函数关系式为y=ax2+k,由题意可知
抛物线与x轴的两个交点坐标为(-4,0),(4,0),且经过点(3,
4),由此三点可得抛物线的关系式为 ,当x=0时,
≈9.1,故该大学校门的高度约为9.1 m.1.下列关于二次函数y=-3x2+2的图象和性质的说法正确的是
( )
(A)开口方向向下,顶点坐标为(0,0)
(B)开口方向向上,对称轴为y轴
(C)y随x的增大而增大
(D)当x>0时,y随x的增大而减小【解析】选D.根据二次函数y=ax2+k的图象和性质,由-3<0可知
开口方向向下,顶点坐标为(0,2),对称轴为y轴;当x>0时,y随x的
增大而减小,当x<0时,y随x的增大而增大.2.在同一坐标系中,一次函数y=ax+1与二次函
数y=x2+a的图象可能是( )【解析】选C.本题考查函数的图象与性质,先根据一次函数
y=ax+1过(0,1)点排除D;再根据二次函数y=x2+a开口向上,排除
B;当a>0时,A,C均不可能,当a<0时,A不可能,只有C可能.所
以答案为C.3.抛物线y=3x2-1的顶点坐标为_______,对称轴是_______.
【解析】因为函数y=ax2+k的顶点坐标为(0,k),对称轴为y轴,所以抛物线y=3x2-1的顶点坐标为(0,-1),对称轴为y轴.
答案:(0,-1) y轴4.廊桥是我国古老的文化遗产.如图是某座抛物线形廊桥的示意
图,已知抛物线的函数关系式为 .为保护廊桥的安
全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,
则这两盏灯的水平距离EF是_____米.(精确到1米)【解析】由“在该抛物线上距水面AB高为8米的点”,
可知y=8,
把y=8代入 得:
x=
由此可求出EF= ≈18(米).
答案:185.若二次函数y=ax2+2的图象经过点(-2,10),求a的值,这个函数有最大值还是最小值?是多少?
【解析】把x=-2,y=10代入y=ax2+2,得4a+2=10,a=2,
∵a=2>0,则抛物线开口向上,有最小值,该函数的最小值是2.
(1)通过在同一坐标系中画函数 与 的图象,可以
得到:它们的对称轴都是__轴(直线____);开口方向都是开口
_____;顶点不同,函数 的顶点坐标为______,
的顶点坐标为______.yx=0向上(0,0)(0,1)(2)通过观察二次函数 与 的图象还可以得到:
当自变量x取同一数值时,函数 的函数值都比 的
函数值____,从图象位置上看,函数 的图象上每一点都
在函数 的图象上相应点的上方_____单位.函数
的图象可以看成是将函数 的图象向___平移___个单位得
到的. 大1一个上一2.二次函数y=ax2+k的性质 向上向下(0,k)(0,k)增大减小减小增大0k0k【点拨】k的符号决定抛物线的顶点在x轴的上方还是下方. yy【预习思考】函数y=x2与y=-x2+1的图象形状是否相同?
提示:它们的形状相同,只是开口方向不同,顶点坐标也不相
同. 二次函数y=ax2+k的图象与性质
【例1】已知下列函数.
y=3x2;y=3x2+2;y=-3x2;y=3x2-2.
(1)指出以上四个二次函数的开口方向、对称轴、顶点坐标及最
值;
(2)函数y=3x2的图象分别与y=3x2+2,y=3x2-2的图象有怎样的联
系?【解题探究】(1)将四个二次函数的图象在平面直角坐标系中分
别画出. 可得:①y=3x2,y=3x2+2与y=3x2-2的开口向上,y=-3x2的开口
向下.
②四个二次函数图象的对称轴均为y轴.
③y=3x2和y=-3x2的顶点坐标为(0,0).y=3x2+2的顶点坐标为
(0,2),y=3x2-2的顶点坐标为(0,-2).
④y=3x2,当x=0时,y最小值=0.
y=3x2+2,当x=0时,y最小值=2.
y=-3x2,当x=0时,y最大值=0.
y=3x2-2,当x=0时,y最小值=-2. (2)通过观察图象可得:
y=3x2+2的图象是将y=3x2的图象向上平移2个单位得到的,
y=3x2-2的图象是将y=3x2的图象向下平移2个单位得到的.【互动探究】函数y=3x2+2的图象经过怎样的平移可得到函数
y=3x2-2的图象?
提示:函数y=3x2+2的图象沿y轴向下平移4个单位可得到函数
y=3x2-2的图象.【规律总结】
函数y=ax2+k的性质口诀
a大于0,口向上,y轴左减右是增,x为0,k最小;
a小于0,口向下,y轴左增右是减,x为0,k最大. 【跟踪训练】
1.抛物线y=-2x2+1的对称轴是( )
(A)直线 (B)直线
(C)y轴 (D)直线x=2
【解析】选C.根据二次函数y=ax2+k的性质可知y=-2x2+1的对称
轴是y轴. 2.下列函数的图象在每一个象限内,y值随x值
的增大而增大的是( )
(A)y=-x+1 (B)y=x2-1
(C)y= (D)【解析】选D.A:对于一次函数y=-x+1,k<0,函数的图象在每一
个象限内,y值随x值的增大而减小,故本选项错误;B:对于二次
函数y=x2-1,当x>0时,y值随x值的增大而增大,当x<0时,y值随
x值的增大而减小,故本选项错误;C:对于反比例函数 ,
k>0,函数的图象在每一个象限内,y值随x值的增大而减小,故本
选项错误;D:对于反比例函数 ,k<0,函数的图象在每一
个象限内,y值随x值的增大而增大,故本选项正确.【变式训练】若二次函数 与y=-x2+k的图象的顶点重
合,则下列结论不正确的是( )
(A)这两个函数图象有相同的对称轴
(B)这两个函数图象的开口方向相反
(C)方程-x2+k=0没有实数根
(D)二次函数y=-x2+k的最大值为
【解析】选C.∵二次函数 与y=-x2+k的图象的顶点重
合,∴ ,∴A,B,D正确;当 时,方程-x2+k=0有实数
根,故C不正确. 3.将抛物线y=x2的图象向上平移1个单位,则
平移后的抛物线的关系式为____________.
【解析】∵图象向上(下)平移,横坐标不变,
∴由题意得,y=x2+1.
答案:y=x2+1 二次函数y=ax2+k的性质的应用
【例2】如图,小河上有一拱桥,拱桥
及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,
ED,DB组成,已知河底ED是水平的,ED=16 m,AE=8 m,抛物线
的顶点C到ED的距离是11 m,以ED所在的直线为x轴,抛物线的
对称轴为y轴建立平面直角坐标系. (1)求抛物线的函数关系式;
(2)已知从某时刻开始的40 h内,水面与河底ED的距离h(单位:m)
随时间t(单位:h)的变化满足函数关系h= (0≤
t≤40)且当水面到顶点C的距离不大于5 m时,需禁止船只通行,
请通过计算说明:在这一时段内,需多少小时禁止船只通行? 【规范解答】(1)设抛物线所对应的函数关系式为y=ax2+11,
由题意得B(8,8),…………………………………………2分
∴64a+11=8,解得a= ,………………………………3分
∴ .………………………………………4分(2)水面到顶点C的距离不大于5 m时,即水面与河底ED的距离h
至少为6m,
∴6= ,……………………………………5分
解得t1=35,t2=3,…………………………………………6分
∴需要35-3=32(h).
答:需32小时禁止船只通行.……………………………7分【规律总结】
利用y=ax2+k的图象及性质解决生活中实际问题的步骤
1.首先建立适当的坐标系.
2.根据图象上的点确定函数关系式.
3.利用抛物线的特点与性质解决具体问题.【跟踪训练】
4.赵州桥的桥拱是抛物线形,建立如
图所示的坐标系,其对应的函数关系
式为 ,当水位线在AB位置时,
水面宽AB=30米,这时水面离桥顶的高
度h是( )
(A)5米 (B)6米 (C)8米 (D)9米
【解析】选D.y= ,|-9|=9.5.隧道的截面是抛物线,且抛物线所对应的函数关系式为
,一辆车高3 m,宽4 m,该车______(填写“能”
或“不能”)通过隧道.
【解析】在 中,
当y=3时, ,解得:
x=± ,所以宽是 <4 m,即不能通过.
答案:不能6.如图,某大学校门是一抛物线形水泥建筑物,大门的地面宽度
为8 m,两侧距地面4 m高处各挂一个牌匾,且两牌匾顶部的水平
距离为6 m,则该大学校门的高度约是多少?(精确到 0.1,建筑厚
度不计)【解析】以校门所在地面线段的中点为原点建立平面直角坐标
系,如图,设抛物线所对应的函数关系式为y=ax2+k,由题意可知
抛物线与x轴的两个交点坐标为(-4,0),(4,0),且经过点(3,
4),由此三点可得抛物线的关系式为 ,当x=0时,
≈9.1,故该大学校门的高度约为9.1 m.1.下列关于二次函数y=-3x2+2的图象和性质的说法正确的是
( )
(A)开口方向向下,顶点坐标为(0,0)
(B)开口方向向上,对称轴为y轴
(C)y随x的增大而增大
(D)当x>0时,y随x的增大而减小【解析】选D.根据二次函数y=ax2+k的图象和性质,由-3<0可知
开口方向向下,顶点坐标为(0,2),对称轴为y轴;当x>0时,y随x的
增大而减小,当x<0时,y随x的增大而增大.2.在同一坐标系中,一次函数y=ax+1与二次函
数y=x2+a的图象可能是( )【解析】选C.本题考查函数的图象与性质,先根据一次函数
y=ax+1过(0,1)点排除D;再根据二次函数y=x2+a开口向上,排除
B;当a>0时,A,C均不可能,当a<0时,A不可能,只有C可能.所
以答案为C.3.抛物线y=3x2-1的顶点坐标为_______,对称轴是_______.
【解析】因为函数y=ax2+k的顶点坐标为(0,k),对称轴为y轴,所以抛物线y=3x2-1的顶点坐标为(0,-1),对称轴为y轴.
答案:(0,-1) y轴4.廊桥是我国古老的文化遗产.如图是某座抛物线形廊桥的示意
图,已知抛物线的函数关系式为 .为保护廊桥的安
全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,
则这两盏灯的水平距离EF是_____米.(精确到1米)【解析】由“在该抛物线上距水面AB高为8米的点”,
可知y=8,
把y=8代入 得:
x=
由此可求出EF= ≈18(米).
答案:185.若二次函数y=ax2+2的图象经过点(-2,10),求a的值,这个函数有最大值还是最小值?是多少?
【解析】把x=-2,y=10代入y=ax2+2,得4a+2=10,a=2,
∵a=2>0,则抛物线开口向上,有最小值,该函数的最小值是2.
