2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第4课时课件(44张ppt)
文档属性
| 名称 | 2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第4课时课件(44张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 11:14:14 | ||
图片预览








文档简介
课件44张PPT。第4课时 1.二次函数y=ax2+bx+c的图象
在坐标系中画出函数y=x2+2x+3的图象
由于y=x2+2x+3可化为y=(x+1)2+2,所以y=x2+2x+3的图象的开口
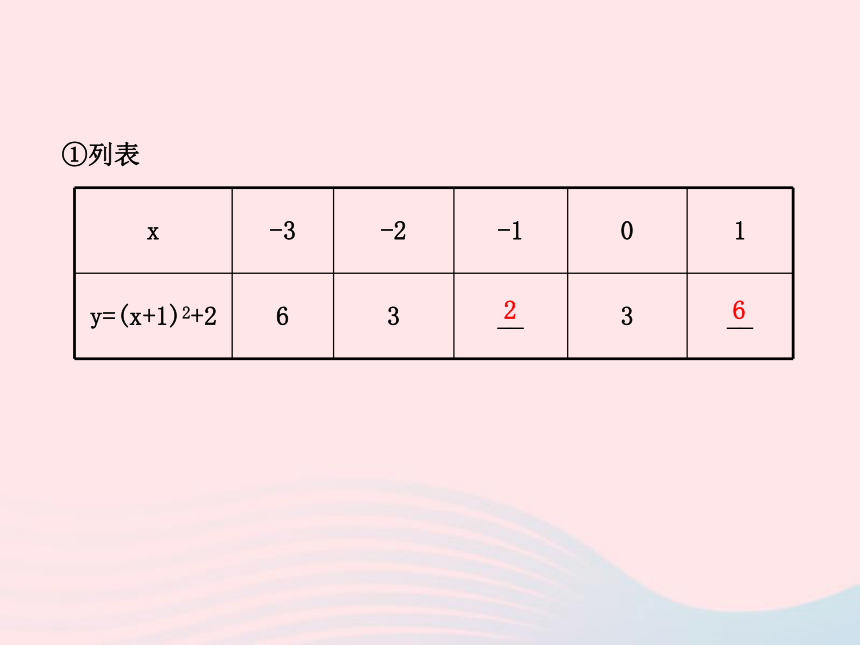
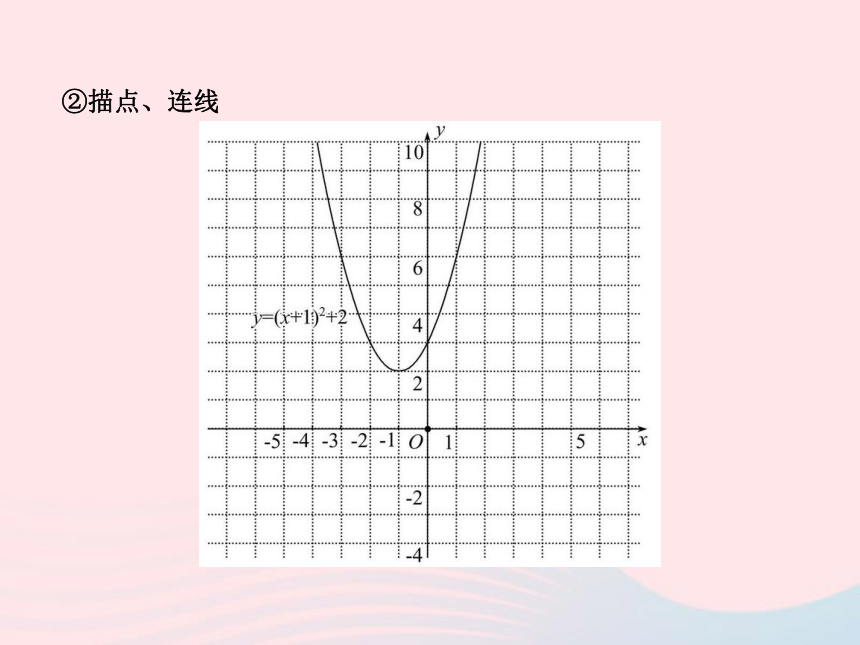
向上,对称轴为x=-1,顶点坐标为(-1,2).①列表26②描点、连线 观察表格和图象:
(1)从图象可以看出函数y=(x+1)2+2的图象是一条_______,开口
方向向___,对称轴是x=___,顶点坐标为(___,2);
(2)当x<___时,函数值y随x的增大而减小;当x>-1时,函数值
y随x的增大而_____;当x=-1时,函数有最___值,最小值为y=__.抛物线上-1-1-1增大小22.二次函数y=ax2+bx+c的性质
(1)把y=ax2+bx+c化为y=a(x-h)2+k的形式.
y=ax2+bx+c______________________________由于y=ax2+bx+c可变形为 ,具有y=a(x-
h)2+k的形式,所以它的图象是_______,h= ,k= .抛物线____________(2)函数y=ax2+bx+c与函数y=ax2的联系及它的对称轴和顶点坐
标.
①函数y=ax2+bx+c的图象是一条抛物线,形状与y=ax2相同,只
是位置不同;
②函数y=ax2+bx+c(a≠0)的对称轴为直线 ,顶点坐标为
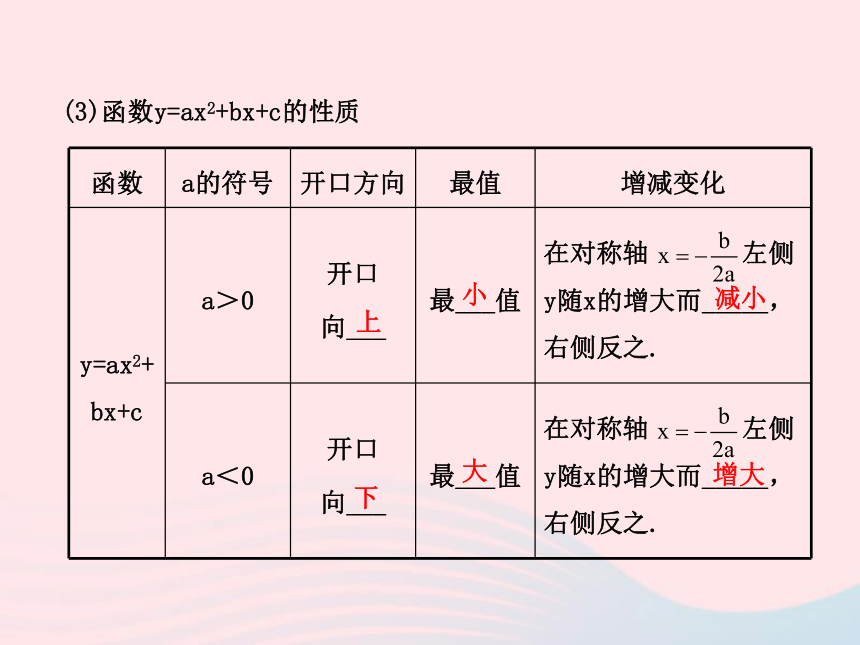
.____________(3)函数y=ax2+bx+c的性质上小减小下大增大【点拨】对于二次函数y=ax2+bx+c,它的顶点坐标和对称轴只
与a,b,c有关.
【预习思考】二次函数y=ax2+bx+c中的c的值能决定它的抛物线
的什么位置?
提示:抛物线y=ax2+bx+c与y轴的交点坐标为(0,c),所以二次函
数y=ax2+bx+c中的c的值能决定抛物线与y轴的交点的位置. 抛物线y=ax2+bx+c的图象与性质
【例1】已知抛物线y=-x2+2x+2.
(1)该抛物线的对称轴是______,顶点坐标是______;
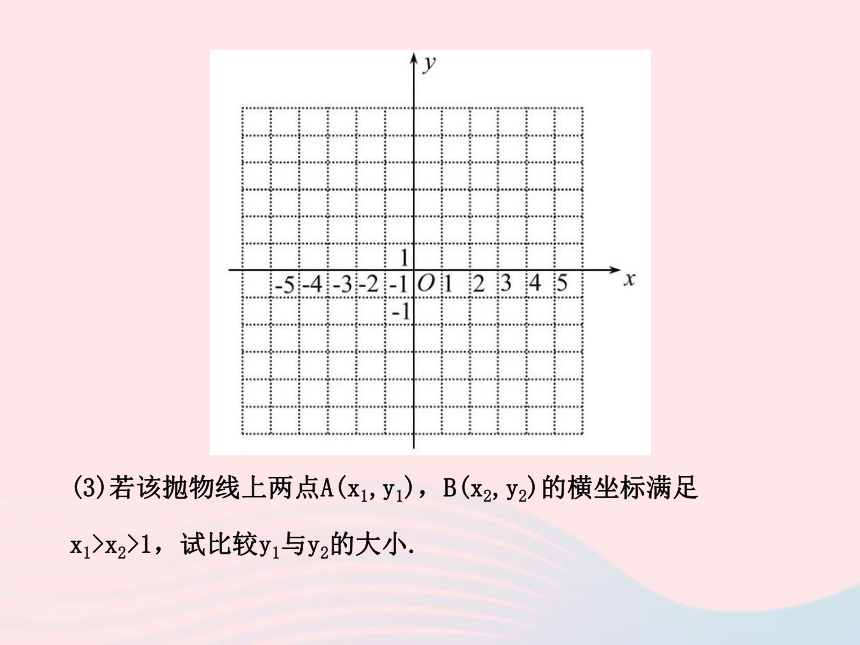
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画
出该抛物线的图象;(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足
x1>x2>1,试比较y1与y2的大小.【解题探究】(1)把抛物线y=-x2+2x+2化成y=a(x-h)2+k(a≠0)
的形式为y=-(x-1)2+3,所以抛物线y=-x2+2x+2的对称轴是
x=1,顶点坐标是(1,3). (2)由于抛物线y=-x2+2x+2的对称轴是x=1,所以选取适当的x值
时要以1为中心,左右再各取两个值,最少取5个值,因此可填表
如下:描点、连线,可得到如图所示的抛物线: (3)因为抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足
x1>x2>1,所以这两点在对称轴x=1的右侧.由抛物线y=-x2+2x+2
的性质可知,在对称轴x=1右侧,y随x的增大而减小,又因为
x1>x2>1,所以y1在画二次函数的图象及理解图象性质时应注意的问题
1.画函数图象时,若抛物线与x轴有交点,最好选取交点描点,
尤其是在作抛物线草图时应抓住以下五个关键点:开口方向,
对称轴,顶点,与x轴的交点,与y轴的交点.
2.列表时应以对称轴为中心选值,间距要适当,描点画图时要
依据已知抛物线的特点,一般先找出特殊点,并用虚线画出
对称轴,然后再对称描点连线.
3.在理解和记忆二次函数的性质时,要结合图象,做到数形结合.【跟踪训练】
1.对于二次函数y=2(x+1)(x-3),下列说法
正确的是( )
(A)图象的开口向下
(B)当x>1时,y随x的增大而减小
(C)当x<1时,y随x的增大而减小
(D)图象的对称轴是直线x=-1【解析】选C.二次函数y=2(x+1)(x-3)可化为y=2x2-4x-6的形式,
可得二次函数的对称轴为
∵此二次函数中a=2>0,∴抛物线开口向上,故A选项错误;∵由二
次函数的关系式可知,此抛物线开口向上,对称轴为x=1,∴当x>1
时,y随x的增大而增大,故B选项错误;∵由二次函数的关系式可
知,此抛物线开口向上,对称轴为x=1,∴当x<1时,y随x的增大而
减小,故C选项正确;二次函数的对称轴为x=1,故D选项错误.2.抛物线y=x2-2x-3的顶点坐标是______.
【解析】方法一:对于一般形式的抛物线方程,通过配方可化
为顶点式y=a(x+h)2+k的形式,从而得到顶点坐标;具体变形为
y=(x-1)2-4,所以顶点坐标为(1,-4).
方法二:直接用抛物线的顶点坐标
答案:(1,-4)3.已知二次函数y=x2-6x+m的最小值为1,那么m的值是_____.
【解析】函数的最小值即顶点的纵坐标,
因为a=1,b=-6,c=m,所以
即
答案:10 抛物线y=ax2+bx+c与a,b,c的符号的关系
【例2】(8分)如图为二次函数y=ax2+bx+c的图象,试判断a,b,c
及b2-4ac的正负.【规范解答】∵抛物线开口向上,∴a>0.………………2分
∵对称轴 ………………………………4分
∵抛物线与y轴交点在x轴下方,∴c<0.…………………6分
∵抛物线与x轴有两个交点,
∴当y=0时,方程ax2+bx+c=0有两个不同的解,
即b2-4ac>0.…………………………………………………8分【互动探究】1.通过观察抛物线y=ax2+bx+c在坐标系中的位
置,当x=1时,可以确定的数值是什么?
提示:通过观察抛物线y=ax2+bx+c在坐标系中的位置,当x=1
时,可以确定a+b+c的值.2.通过观察抛物线y=ax2+bx+c在坐标系中的位置,当x=-1时,
可以确定的数值是什么?
提示:通过观察抛物线y=ax2+bx+c在坐标系中的位置,当x=-1
时,可以确定a-b+c的值.【规律总结】
二次函数y=ax2+bx+c的图象的特征与a,b,c的符号之间的关系
1.a决定开口方向和大小:
(1)a>0?开口向上;
(2)a<0?开口向下;
(3)|a|相同时,抛物线形状相同,|a|越大,抛物线开口越小.2.a,b决定对称轴位置:
(1)b=0?对称轴为y轴;
(2)a,b同号?对称轴在y轴左侧;
(3)a,b异号?对称轴在y轴右侧.
3.c决定抛物线与y轴的交点位置:
(1)c=0?过原点;
(2)c>0?交点在y轴的正半轴上;
(3)c<0?交点在y轴的负半轴上. 【跟踪训练】
4.已知抛物线y=ax2+bx+c(a≠0)在平面
直角坐标系中的位置如图所示,则下列结论中正确的是( )
(A)a>0 (B)b<0
(C)c<0 (D)a+b+c>0【解析】选D.因为抛物线开口向下,二次项系数a<0,所以A
项错误;根据对称轴方程x ,a<0,所以b>0,所以B项
错误;因为抛物线与y轴的交点在x轴上方,所以c>0,所以C
项错误;因为直线x=1与抛物线的交点在x轴上方,所以x=1时,
函数值y=a+b+c>0,所以D项正确.5.小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出
了下面五条信息:(1)a<0;(2)c>1;(3)b>0;(4)a+b+c>
0;(5)a-b+c>0.你认为其中正确的信息有( )
(A)2个 (B)3个 (C)4个 (D)5个【解析】选C.(1)由抛物线的开口向下知a<0,故正确;(2)由
抛物线与y轴的交点在y轴的正半轴上且大于1,可推出c>1,故
正确;(3)由图可知对称轴为 ,可推出a,b异号,又
∵a<0,∴b>0,故正确;
(4)由抛物线与x轴的交点可以看出,当x=1时,y>0,所以
a+b+c>0,故正确;
(5)由抛物线与x轴的交点可以看出,当x=-1时,y<0,所以
a-b+c<0,故错误.【变式训练】如图,抛物线y=ax2+bx+c的对称轴是x= ,小亮通
过观察得出了下面四条信息:
①c<0,②abc<0,③a-b+c>0,④2a-3b=0.你认为其中正确
的有( )
(A)1个 (B)2个 (C)3个 (D)4个【解析】选B.①由抛物线与y轴的交点在y轴的负半轴上,可知
c<0,正确;
②由抛物线的开口向上知,a>0,对称轴为 ,a,b异
号,即b<0,∴abc>0,错误;
③当x=-1时,y=a-b+c>0,正确;
④由对称轴为 得2a+3b=0,错误.6.已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一
象限.有下列三个结论:①a<0;②a+b+c>0;③ 把
正确结论的序号填在横线上______________.【解析】由抛物线开口向下可推出a<0;因为对称轴在y轴右,
对称轴为
由图象可知:当x=1时,y>0,∴a+b+c>0.
∴①②③都正确.
答案:①②③ 1.如图,二次函数的图象经过(-2,-1),(1,1)
两点,则下列关于此二次函数的说法正确的是( )
(A)y的最大值小于0 (B)当x=0时,y的值大于1
(C)当x=-1时,y的值大于1 (D)当x=-3时,y的值小于0【解析】选D.由图象知,点(1,1)在图象的对称轴的左边,所以y
的最大值大于1,不小于0,故A项错误;由图象知,当x=0时,y的值
就是函数图象与y轴的交点,而图象与y轴的交点在(1,1)点的左
边,故y<1,故B项错误;对称轴在(1,1)的右边,在对称轴的左边y
随x的增大而增大,∵-1<1,∴x=-1时,y的值小于1,故C项错误;
当x=-3时,函数图象上的点在点(-2,-1)的左边,所以y的值小于
0,故D项正确.2.若二次函数y=x2-6x+c的图象过A(-1,y1),
B(2,y2),C(3+ ,y3) 三点,则y1,y2,y3的大小关系正确的是
( )
(A)y1>y2>y3 (B)y1>y3>y2
(C)y2>y1>y3 (D)y3>y1>y2【解析】选B.方法一:y=x2-6x+c=
(x-3)2-9+c,对称轴为直线
x=3.如图可得出y1>y3>y2.
方法二:把A,B,C三点坐标分别代入关系
式,化简得:y1=7+c,y2=-8+c,y3=-7+c.
所以y1>y3>y2.故选B.3.将二次函数y=x2-4x+5化为y=(x-h)2+k的形
式,则y=______________.
【解析】y=x2-4x+5=x2-4x+4-4+5=(x-2)2+1.
答案:(x-2)2+14.已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在
第_____象限.【解析】∵抛物线的开口向下,∴a<0,
∵对称轴在y轴左边,
∴a,b同号即b<0,
∵抛物线与y轴的交点在正半轴,
∴c>0,∴bc<0,
∴点P(a,bc)在第三象限.
答案:三5.已知抛物线
(1)确定此抛物线的顶点在第几象限;
(2)确定此抛物线的对称轴;
(3)假设抛物线经过原点,求抛物线的顶点坐标.【解析】(1)
其顶点坐标为 而
所以顶点在第二象限.
(2)其对称轴为直线x=-1.
(3)若抛物线过原点(0,0),
则
∴顶点坐标为(-1,1).
在坐标系中画出函数y=x2+2x+3的图象
由于y=x2+2x+3可化为y=(x+1)2+2,所以y=x2+2x+3的图象的开口
向上,对称轴为x=-1,顶点坐标为(-1,2).①列表26②描点、连线 观察表格和图象:
(1)从图象可以看出函数y=(x+1)2+2的图象是一条_______,开口
方向向___,对称轴是x=___,顶点坐标为(___,2);
(2)当x<___时,函数值y随x的增大而减小;当x>-1时,函数值
y随x的增大而_____;当x=-1时,函数有最___值,最小值为y=__.抛物线上-1-1-1增大小22.二次函数y=ax2+bx+c的性质
(1)把y=ax2+bx+c化为y=a(x-h)2+k的形式.
y=ax2+bx+c______________________________由于y=ax2+bx+c可变形为 ,具有y=a(x-
h)2+k的形式,所以它的图象是_______,h= ,k= .抛物线____________(2)函数y=ax2+bx+c与函数y=ax2的联系及它的对称轴和顶点坐
标.
①函数y=ax2+bx+c的图象是一条抛物线,形状与y=ax2相同,只
是位置不同;
②函数y=ax2+bx+c(a≠0)的对称轴为直线 ,顶点坐标为
.____________(3)函数y=ax2+bx+c的性质上小减小下大增大【点拨】对于二次函数y=ax2+bx+c,它的顶点坐标和对称轴只
与a,b,c有关.
【预习思考】二次函数y=ax2+bx+c中的c的值能决定它的抛物线
的什么位置?
提示:抛物线y=ax2+bx+c与y轴的交点坐标为(0,c),所以二次函
数y=ax2+bx+c中的c的值能决定抛物线与y轴的交点的位置. 抛物线y=ax2+bx+c的图象与性质
【例1】已知抛物线y=-x2+2x+2.
(1)该抛物线的对称轴是______,顶点坐标是______;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画
出该抛物线的图象;(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足
x1>x2>1,试比较y1与y2的大小.【解题探究】(1)把抛物线y=-x2+2x+2化成y=a(x-h)2+k(a≠0)
的形式为y=-(x-1)2+3,所以抛物线y=-x2+2x+2的对称轴是
x=1,顶点坐标是(1,3). (2)由于抛物线y=-x2+2x+2的对称轴是x=1,所以选取适当的x值
时要以1为中心,左右再各取两个值,最少取5个值,因此可填表
如下:描点、连线,可得到如图所示的抛物线: (3)因为抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足
x1>x2>1,所以这两点在对称轴x=1的右侧.由抛物线y=-x2+2x+2
的性质可知,在对称轴x=1右侧,y随x的增大而减小,又因为
x1>x2>1,所以y1
1.画函数图象时,若抛物线与x轴有交点,最好选取交点描点,
尤其是在作抛物线草图时应抓住以下五个关键点:开口方向,
对称轴,顶点,与x轴的交点,与y轴的交点.
2.列表时应以对称轴为中心选值,间距要适当,描点画图时要
依据已知抛物线的特点,一般先找出特殊点,并用虚线画出
对称轴,然后再对称描点连线.
3.在理解和记忆二次函数的性质时,要结合图象,做到数形结合.【跟踪训练】
1.对于二次函数y=2(x+1)(x-3),下列说法
正确的是( )
(A)图象的开口向下
(B)当x>1时,y随x的增大而减小
(C)当x<1时,y随x的增大而减小
(D)图象的对称轴是直线x=-1【解析】选C.二次函数y=2(x+1)(x-3)可化为y=2x2-4x-6的形式,
可得二次函数的对称轴为
∵此二次函数中a=2>0,∴抛物线开口向上,故A选项错误;∵由二
次函数的关系式可知,此抛物线开口向上,对称轴为x=1,∴当x>1
时,y随x的增大而增大,故B选项错误;∵由二次函数的关系式可
知,此抛物线开口向上,对称轴为x=1,∴当x<1时,y随x的增大而
减小,故C选项正确;二次函数的对称轴为x=1,故D选项错误.2.抛物线y=x2-2x-3的顶点坐标是______.
【解析】方法一:对于一般形式的抛物线方程,通过配方可化
为顶点式y=a(x+h)2+k的形式,从而得到顶点坐标;具体变形为
y=(x-1)2-4,所以顶点坐标为(1,-4).
方法二:直接用抛物线的顶点坐标
答案:(1,-4)3.已知二次函数y=x2-6x+m的最小值为1,那么m的值是_____.
【解析】函数的最小值即顶点的纵坐标,
因为a=1,b=-6,c=m,所以
即
答案:10 抛物线y=ax2+bx+c与a,b,c的符号的关系
【例2】(8分)如图为二次函数y=ax2+bx+c的图象,试判断a,b,c
及b2-4ac的正负.【规范解答】∵抛物线开口向上,∴a>0.………………2分
∵对称轴 ………………………………4分
∵抛物线与y轴交点在x轴下方,∴c<0.…………………6分
∵抛物线与x轴有两个交点,
∴当y=0时,方程ax2+bx+c=0有两个不同的解,
即b2-4ac>0.…………………………………………………8分【互动探究】1.通过观察抛物线y=ax2+bx+c在坐标系中的位
置,当x=1时,可以确定的数值是什么?
提示:通过观察抛物线y=ax2+bx+c在坐标系中的位置,当x=1
时,可以确定a+b+c的值.2.通过观察抛物线y=ax2+bx+c在坐标系中的位置,当x=-1时,
可以确定的数值是什么?
提示:通过观察抛物线y=ax2+bx+c在坐标系中的位置,当x=-1
时,可以确定a-b+c的值.【规律总结】
二次函数y=ax2+bx+c的图象的特征与a,b,c的符号之间的关系
1.a决定开口方向和大小:
(1)a>0?开口向上;
(2)a<0?开口向下;
(3)|a|相同时,抛物线形状相同,|a|越大,抛物线开口越小.2.a,b决定对称轴位置:
(1)b=0?对称轴为y轴;
(2)a,b同号?对称轴在y轴左侧;
(3)a,b异号?对称轴在y轴右侧.
3.c决定抛物线与y轴的交点位置:
(1)c=0?过原点;
(2)c>0?交点在y轴的正半轴上;
(3)c<0?交点在y轴的负半轴上. 【跟踪训练】
4.已知抛物线y=ax2+bx+c(a≠0)在平面
直角坐标系中的位置如图所示,则下列结论中正确的是( )
(A)a>0 (B)b<0
(C)c<0 (D)a+b+c>0【解析】选D.因为抛物线开口向下,二次项系数a<0,所以A
项错误;根据对称轴方程x ,a<0,所以b>0,所以B项
错误;因为抛物线与y轴的交点在x轴上方,所以c>0,所以C
项错误;因为直线x=1与抛物线的交点在x轴上方,所以x=1时,
函数值y=a+b+c>0,所以D项正确.5.小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出
了下面五条信息:(1)a<0;(2)c>1;(3)b>0;(4)a+b+c>
0;(5)a-b+c>0.你认为其中正确的信息有( )
(A)2个 (B)3个 (C)4个 (D)5个【解析】选C.(1)由抛物线的开口向下知a<0,故正确;(2)由
抛物线与y轴的交点在y轴的正半轴上且大于1,可推出c>1,故
正确;(3)由图可知对称轴为 ,可推出a,b异号,又
∵a<0,∴b>0,故正确;
(4)由抛物线与x轴的交点可以看出,当x=1时,y>0,所以
a+b+c>0,故正确;
(5)由抛物线与x轴的交点可以看出,当x=-1时,y<0,所以
a-b+c<0,故错误.【变式训练】如图,抛物线y=ax2+bx+c的对称轴是x= ,小亮通
过观察得出了下面四条信息:
①c<0,②abc<0,③a-b+c>0,④2a-3b=0.你认为其中正确
的有( )
(A)1个 (B)2个 (C)3个 (D)4个【解析】选B.①由抛物线与y轴的交点在y轴的负半轴上,可知
c<0,正确;
②由抛物线的开口向上知,a>0,对称轴为 ,a,b异
号,即b<0,∴abc>0,错误;
③当x=-1时,y=a-b+c>0,正确;
④由对称轴为 得2a+3b=0,错误.6.已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一
象限.有下列三个结论:①a<0;②a+b+c>0;③ 把
正确结论的序号填在横线上______________.【解析】由抛物线开口向下可推出a<0;因为对称轴在y轴右,
对称轴为
由图象可知:当x=1时,y>0,∴a+b+c>0.
∴①②③都正确.
答案:①②③ 1.如图,二次函数的图象经过(-2,-1),(1,1)
两点,则下列关于此二次函数的说法正确的是( )
(A)y的最大值小于0 (B)当x=0时,y的值大于1
(C)当x=-1时,y的值大于1 (D)当x=-3时,y的值小于0【解析】选D.由图象知,点(1,1)在图象的对称轴的左边,所以y
的最大值大于1,不小于0,故A项错误;由图象知,当x=0时,y的值
就是函数图象与y轴的交点,而图象与y轴的交点在(1,1)点的左
边,故y<1,故B项错误;对称轴在(1,1)的右边,在对称轴的左边y
随x的增大而增大,∵-1<1,∴x=-1时,y的值小于1,故C项错误;
当x=-3时,函数图象上的点在点(-2,-1)的左边,所以y的值小于
0,故D项正确.2.若二次函数y=x2-6x+c的图象过A(-1,y1),
B(2,y2),C(3+ ,y3) 三点,则y1,y2,y3的大小关系正确的是
( )
(A)y1>y2>y3 (B)y1>y3>y2
(C)y2>y1>y3 (D)y3>y1>y2【解析】选B.方法一:y=x2-6x+c=
(x-3)2-9+c,对称轴为直线
x=3.如图可得出y1>y3>y2.
方法二:把A,B,C三点坐标分别代入关系
式,化简得:y1=7+c,y2=-8+c,y3=-7+c.
所以y1>y3>y2.故选B.3.将二次函数y=x2-4x+5化为y=(x-h)2+k的形
式,则y=______________.
【解析】y=x2-4x+5=x2-4x+4-4+5=(x-2)2+1.
答案:(x-2)2+14.已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在
第_____象限.【解析】∵抛物线的开口向下,∴a<0,
∵对称轴在y轴左边,
∴a,b同号即b<0,
∵抛物线与y轴的交点在正半轴,
∴c>0,∴bc<0,
∴点P(a,bc)在第三象限.
答案:三5.已知抛物线
(1)确定此抛物线的顶点在第几象限;
(2)确定此抛物线的对称轴;
(3)假设抛物线经过原点,求抛物线的顶点坐标.【解析】(1)
其顶点坐标为 而
所以顶点在第二象限.
(2)其对称轴为直线x=-1.
(3)若抛物线过原点(0,0),
则
∴顶点坐标为(-1,1).
