2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第2课时 课件(25张PPT)
文档属性
| 名称 | 2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第2课时 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览







文档简介
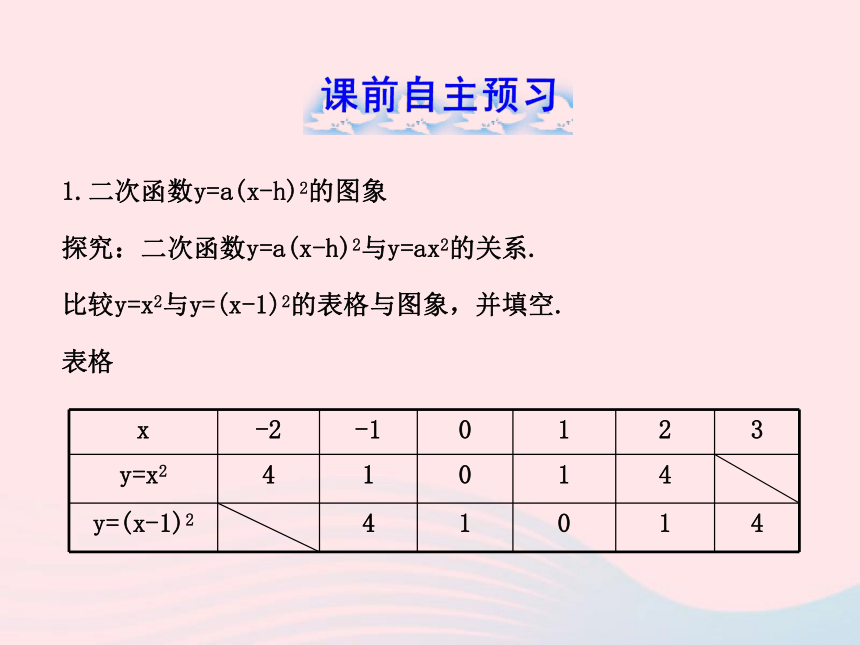
课件25张PPT。第2课时 1.二次函数y=a(x-h)2的图象
探究:二次函数y=a(x-h)2与y=ax2的关系.
比较y=x2与y=(x-1)2的表格与图象,并填空.
表格图象(1)从表格可以看出,当函数值相等时,y=(x-1)2的自变量的值
比y=x2的自变量的值____.
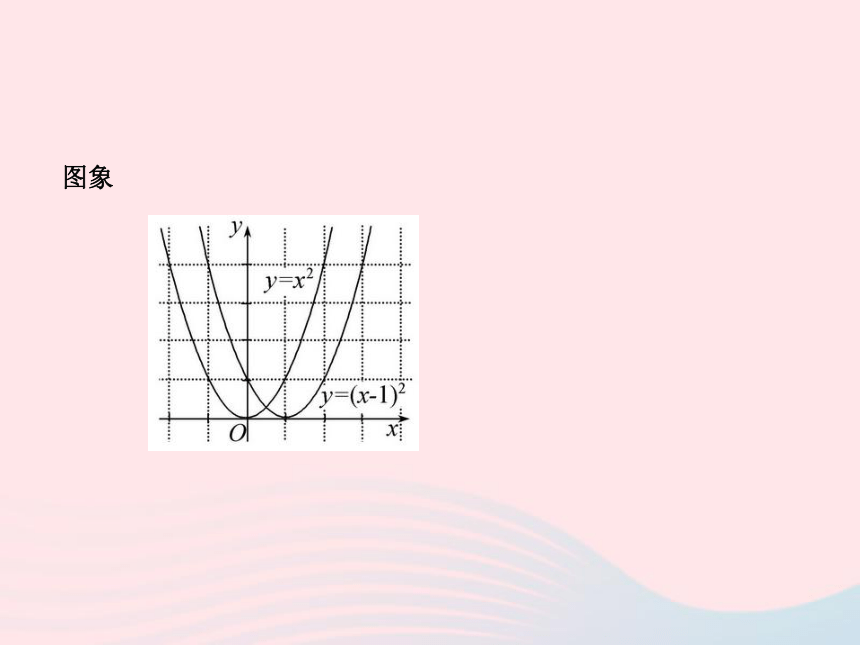
(2)从图象可以看出,只需要把y=x2的图象向___平移__个单位就
可得到y=(x-1)2的图象.
(3)①二次函数y=a(x-h)2的图象是_______,它与抛物线y=ax2的
_____相同,只是_____不同;
②二次函数y=a(x-h)2的对称轴为直线____,顶点坐标为_______.大1右1抛物线形状位置x=h(h,0)2.二次函数y=a(x-h)2的性质
(1)a>0:当x___时,函数值y随x的增大而减小;当x___时,函数值
y随x的增大而增大;
当x=__时,函数取得最___值,最___值为y=__.
(2)a<0:当x___时,函数值y随x的增大而增大;当x___时,函数值
y随x的增大而减小;
当x=__时,函数取得最___值,最___值为y=__.h小小0hh大大0h【点拨】y=ax2 y=a(x-h)2.【预习思考】
函数y=-(x-3)2与函数y=-(x+3)2的图象有怎样的联系?
提示:函数y=-(x-3)2的图象可由y=-(x+3)2的图象向右平移6个
单位得到,或函数y=-(x+3)2的图象可由y=-(x-3)2的图象向左平
移6个单位得到. 抛物线y=a(x-h)2与y=ax2的平移
【例1】已知抛物线y=a(x-h)2向左平移2个单位后,所得抛物线
为y=-2(x+5)2,试求a,h的值.
【解题探究】
(1)抛物线左右平移对a的值有影响吗?a的值为多少?
答:抛物线左右平移对a的值没有影响,a=-2.(2)对于抛物线平移的问题可以(填“可以”或“不可以”)转化
为抛物线顶点的平移.
(3)y=a(x-h)2的顶点坐标为(h,0),y=-2(x+5)2的顶点坐标为
(-5,0),将点(h,0)向左平移2个单位后为(h-2,0),所以h-2=-5,
得h=-3.
(4)综上可知a=-2,h=-3. 【规律总结】
函数y=a(x-h)2图象的左右平移规律
函数y=a(x-h)2图象的左右平移中a是不变的,向左平移m个单位
则为y=a(x-h+m)2,向右平移m个单位则为y=a(x-h-m)2,简记为
“左加右减”. 【跟踪训练】
1.将抛物线y=-x2向左平移2个单位后,得到的
抛物线的关系式是( )
(A)y=-(x+2)2 (B)y=-x2+2
(C)y=-(x-2)2 (D)y=-x2-2
【解析】选A.抛物线y=a(x-h)2可以由y=ax2经过适当的平移得到,
自变量值加减左右移,函数值加减上下移.2.在平面直角坐标系中,函数y=-x-1与 的图象大致
是( )
【解析】选A.∵y=-x-1的图象过第二、三、四象限,
的开口向下,顶点为点(1,0),∴同时符合上述条件的图象只有选
项A.3.抛物线y=-10(x+9)2由y=-10x2向_________平移______个单位
可以得到.
【解析】抛物线y=-10(x+9)2的顶点坐标为(-9,0),抛物线
y=-10x2的顶点坐标为(0,0),由(0,0)到(-9,0)是向左平移9个
单位,所以抛物线y=-10(x+9)2由y=-10x2向左平移9个单位可以
得到.
答案:左 9 函数y=a(x-h)2的图象和性质
【例2】(6分)已知函数y=6(x+4)2,
(1)直接写出它的顶点坐标及对称轴;
(2)直接写出向右平移3个单位后的关系式、顶点坐标及对称
轴;
(3)平移后当x取何值时,y随x的增大而增大?当x取何值时,y随x
的增大而减小?
特别提醒:左右平移时注意h值的增减变化.【规范解答】
(1)函数y=6(x+4)2的顶点坐标为(-4,0),对称轴为直线x=-4;
………………………………………………………………2分
(2)向右平移3个单位后的关系式为y=6(x+1)2,顶点坐标为
(-1,0),对称轴为直线x=-1;………………………………4分
(3)因为函数y=6(x+1)2的图象开口向上,所以当x≥-1时,y随x的
增大而增大;当x≤-1时,y随x的增大而减小.……………6分【规律总结】
检验平移后函数关系式是否正确的方法
特殊点法:分别写出两函数的顶点坐标,观察它们的顶点是否也可以通过相同的平移方法得到.【跟踪训练】
4.抛物线y=-3(x-5)2的对称轴是直线______,顶点坐标为_____,
有最___值为_____.
【解析】抛物线y=-3(x-5)2的对称轴是直线x=5,顶点坐标为
(5,0),有最大值为0.
答案:x=5 (5,0) 大 05.函数y=-3(x+1)2,当x______时,函数值y随x的增大而减小;
当x______时,函数有最____值,它是______.
【解析】∵-3<0,∴抛物线开口向下.
其对称轴为直线x=-1,即当x>-1时,y随x的增大而减小;因为抛
物线开口向下,所以当x=-1时,函数有最高点,即最大值,最大
值是0.
答案:≥-1 =-1 大 0【变式训练】关于二次函数y=-(x-2)2的图象,下列说法正确的
是( )
(A)是中心对称图形 (B)开口向上
(C)对称轴是直线x=-2 (D)最高点是(2,0)
【解析】选D.二次函数y=-(x-2)2的图象开口向下,是轴对称图
形,对称轴是x=2,顶点坐标,即最高点是(2,0).1.和抛物线y=-2(x+10)2开口大小相等,方向相反,顶点为(3,0)
的抛物线关系式为( )
(A)y=2(x+3)2 (B)y=2(x-3)2
(C)y=-2(x+3)2 (D)y=-2(x-3)2
【解析】选B.因为其图象和抛物线y=-2(x+10)2开口大小相等,方向相反,所以a=2;又因为抛物线顶点为(3,0),所以抛物线关系式为y=2(x-3)2.2.抛物线y=x2-2x+1的顶点坐标是( )
(A)(1,0) (B)(-1,0)
(C)(-2,1) (D)(2,-1)
【解析】选A.配方得y=(x-1)2,得顶点为(1,0). 3.将抛物线y=2(x-3)2平移得到抛物线y=2(x+3)2,应该向_____
平移_____个单位.
【解析】因为抛物线y=2(x-3)2的顶点坐标为(3,0),抛物线y=2(x+3)2的顶点坐标为(-3,0),所以若将抛物线y=2(x-3)2平移得到抛物线y=2(x+3)2,应该向左平移6个单位.
答案:左 64.函数 的图象是由 的图象向____平移____
个单位得到的,顶点坐标是_______.当x____时,函数值y随x的增大而减小;当x____时,函数值y随x的增大而增大;当x____时,函数取得____值,其值为______.
【解析】函数 的图象是由 的图象向右平移3
个单位得到的.顶点坐标是(3,0).当x>3时,函数值y随x的增大
而减小;当x<3时,函数值y随x的增大而增大;当x=3时,函数取
得最大值,其值为0.
答案:右 3 (3,0) >3 <3 =3 大 05.已知二次函数y=2x2-12x+18.
(1)求该函数图象的开口方向,对称轴以及图象与坐标轴的交点坐标;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?并求出函数的最大值或最小值.【解析】(1)∵y=2x2-12x+18=2(x2-6x+9)=2(x-3)2.
∴开口向上,对称轴是直线x=3,顶点为(3,0),
当x=0时,y=2(x-3)2=2(0-3)2=18,
当y=0时,0=2(x-3)2,解得x=3,
∴二次函数y=2x2-12x+18与x轴的交点为(3,0),与y轴的交点为
(0,18).
(2)当x>3时,y随x的增大而增大;
当x<3时,y随x的增大而减小;
当x=3时,有最小值为0.
探究:二次函数y=a(x-h)2与y=ax2的关系.
比较y=x2与y=(x-1)2的表格与图象,并填空.
表格图象(1)从表格可以看出,当函数值相等时,y=(x-1)2的自变量的值
比y=x2的自变量的值____.
(2)从图象可以看出,只需要把y=x2的图象向___平移__个单位就
可得到y=(x-1)2的图象.
(3)①二次函数y=a(x-h)2的图象是_______,它与抛物线y=ax2的
_____相同,只是_____不同;
②二次函数y=a(x-h)2的对称轴为直线____,顶点坐标为_______.大1右1抛物线形状位置x=h(h,0)2.二次函数y=a(x-h)2的性质
(1)a>0:当x___时,函数值y随x的增大而减小;当x___时,函数值
y随x的增大而增大;
当x=__时,函数取得最___值,最___值为y=__.
(2)a<0:当x___时,函数值y随x的增大而增大;当x___时,函数值
y随x的增大而减小;
当x=__时,函数取得最___值,最___值为y=__.
函数y=-(x-3)2与函数y=-(x+3)2的图象有怎样的联系?
提示:函数y=-(x-3)2的图象可由y=-(x+3)2的图象向右平移6个
单位得到,或函数y=-(x+3)2的图象可由y=-(x-3)2的图象向左平
移6个单位得到. 抛物线y=a(x-h)2与y=ax2的平移
【例1】已知抛物线y=a(x-h)2向左平移2个单位后,所得抛物线
为y=-2(x+5)2,试求a,h的值.
【解题探究】
(1)抛物线左右平移对a的值有影响吗?a的值为多少?
答:抛物线左右平移对a的值没有影响,a=-2.(2)对于抛物线平移的问题可以(填“可以”或“不可以”)转化
为抛物线顶点的平移.
(3)y=a(x-h)2的顶点坐标为(h,0),y=-2(x+5)2的顶点坐标为
(-5,0),将点(h,0)向左平移2个单位后为(h-2,0),所以h-2=-5,
得h=-3.
(4)综上可知a=-2,h=-3. 【规律总结】
函数y=a(x-h)2图象的左右平移规律
函数y=a(x-h)2图象的左右平移中a是不变的,向左平移m个单位
则为y=a(x-h+m)2,向右平移m个单位则为y=a(x-h-m)2,简记为
“左加右减”. 【跟踪训练】
1.将抛物线y=-x2向左平移2个单位后,得到的
抛物线的关系式是( )
(A)y=-(x+2)2 (B)y=-x2+2
(C)y=-(x-2)2 (D)y=-x2-2
【解析】选A.抛物线y=a(x-h)2可以由y=ax2经过适当的平移得到,
自变量值加减左右移,函数值加减上下移.2.在平面直角坐标系中,函数y=-x-1与 的图象大致
是( )
【解析】选A.∵y=-x-1的图象过第二、三、四象限,
的开口向下,顶点为点(1,0),∴同时符合上述条件的图象只有选
项A.3.抛物线y=-10(x+9)2由y=-10x2向_________平移______个单位
可以得到.
【解析】抛物线y=-10(x+9)2的顶点坐标为(-9,0),抛物线
y=-10x2的顶点坐标为(0,0),由(0,0)到(-9,0)是向左平移9个
单位,所以抛物线y=-10(x+9)2由y=-10x2向左平移9个单位可以
得到.
答案:左 9 函数y=a(x-h)2的图象和性质
【例2】(6分)已知函数y=6(x+4)2,
(1)直接写出它的顶点坐标及对称轴;
(2)直接写出向右平移3个单位后的关系式、顶点坐标及对称
轴;
(3)平移后当x取何值时,y随x的增大而增大?当x取何值时,y随x
的增大而减小?
特别提醒:左右平移时注意h值的增减变化.【规范解答】
(1)函数y=6(x+4)2的顶点坐标为(-4,0),对称轴为直线x=-4;
………………………………………………………………2分
(2)向右平移3个单位后的关系式为y=6(x+1)2,顶点坐标为
(-1,0),对称轴为直线x=-1;………………………………4分
(3)因为函数y=6(x+1)2的图象开口向上,所以当x≥-1时,y随x的
增大而增大;当x≤-1时,y随x的增大而减小.……………6分【规律总结】
检验平移后函数关系式是否正确的方法
特殊点法:分别写出两函数的顶点坐标,观察它们的顶点是否也可以通过相同的平移方法得到.【跟踪训练】
4.抛物线y=-3(x-5)2的对称轴是直线______,顶点坐标为_____,
有最___值为_____.
【解析】抛物线y=-3(x-5)2的对称轴是直线x=5,顶点坐标为
(5,0),有最大值为0.
答案:x=5 (5,0) 大 05.函数y=-3(x+1)2,当x______时,函数值y随x的增大而减小;
当x______时,函数有最____值,它是______.
【解析】∵-3<0,∴抛物线开口向下.
其对称轴为直线x=-1,即当x>-1时,y随x的增大而减小;因为抛
物线开口向下,所以当x=-1时,函数有最高点,即最大值,最大
值是0.
答案:≥-1 =-1 大 0【变式训练】关于二次函数y=-(x-2)2的图象,下列说法正确的
是( )
(A)是中心对称图形 (B)开口向上
(C)对称轴是直线x=-2 (D)最高点是(2,0)
【解析】选D.二次函数y=-(x-2)2的图象开口向下,是轴对称图
形,对称轴是x=2,顶点坐标,即最高点是(2,0).1.和抛物线y=-2(x+10)2开口大小相等,方向相反,顶点为(3,0)
的抛物线关系式为( )
(A)y=2(x+3)2 (B)y=2(x-3)2
(C)y=-2(x+3)2 (D)y=-2(x-3)2
【解析】选B.因为其图象和抛物线y=-2(x+10)2开口大小相等,方向相反,所以a=2;又因为抛物线顶点为(3,0),所以抛物线关系式为y=2(x-3)2.2.抛物线y=x2-2x+1的顶点坐标是( )
(A)(1,0) (B)(-1,0)
(C)(-2,1) (D)(2,-1)
【解析】选A.配方得y=(x-1)2,得顶点为(1,0). 3.将抛物线y=2(x-3)2平移得到抛物线y=2(x+3)2,应该向_____
平移_____个单位.
【解析】因为抛物线y=2(x-3)2的顶点坐标为(3,0),抛物线y=2(x+3)2的顶点坐标为(-3,0),所以若将抛物线y=2(x-3)2平移得到抛物线y=2(x+3)2,应该向左平移6个单位.
答案:左 64.函数 的图象是由 的图象向____平移____
个单位得到的,顶点坐标是_______.当x____时,函数值y随x的增大而减小;当x____时,函数值y随x的增大而增大;当x____时,函数取得____值,其值为______.
【解析】函数 的图象是由 的图象向右平移3
个单位得到的.顶点坐标是(3,0).当x>3时,函数值y随x的增大
而减小;当x<3时,函数值y随x的增大而增大;当x=3时,函数取
得最大值,其值为0.
答案:右 3 (3,0) >3 <3 =3 大 05.已知二次函数y=2x2-12x+18.
(1)求该函数图象的开口方向,对称轴以及图象与坐标轴的交点坐标;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?并求出函数的最大值或最小值.【解析】(1)∵y=2x2-12x+18=2(x2-6x+9)=2(x-3)2.
∴开口向上,对称轴是直线x=3,顶点为(3,0),
当x=0时,y=2(x-3)2=2(0-3)2=18,
当y=0时,0=2(x-3)2,解得x=3,
∴二次函数y=2x2-12x+18与x轴的交点为(3,0),与y轴的交点为
(0,18).
(2)当x>3时,y随x的增大而增大;
当x<3时,y随x的增大而减小;
当x=3时,有最小值为0.
