2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第5课时 课件(28张PPT)
文档属性
| 名称 | 2020春华师版九下数学26.2.2二次函数y=ax2+bx+c的图象与性质第5课时 课件(28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 573.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 16:39:05 | ||
图片预览








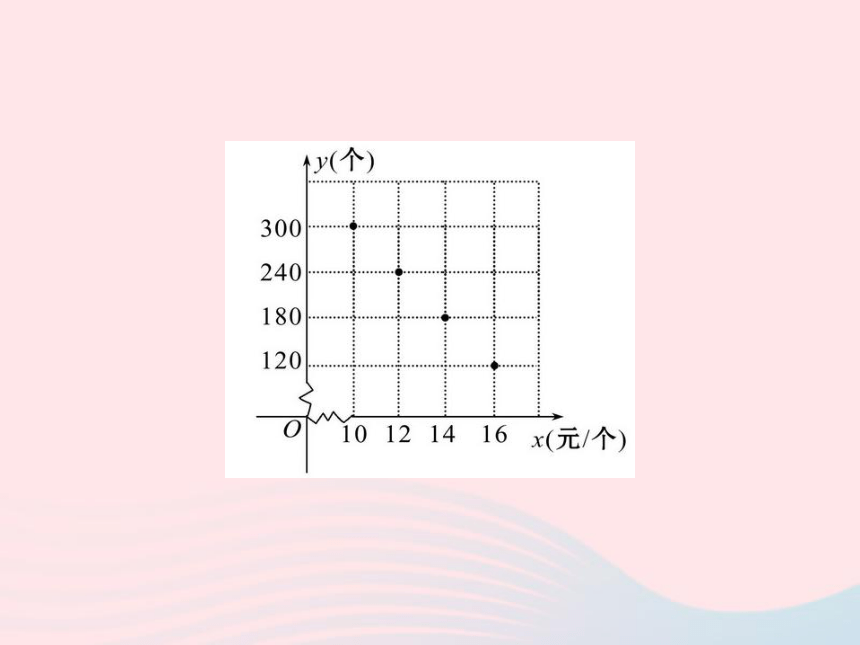
文档简介
课件28张PPT。第5课时1.求二次函数最值的方法
(1)配方法:y=ax2+bx+c化为y=_________的形式,当自变量x=__
时,函数y最大(小)=__.如二次函数y=3x2+6x+4可化为
y=3______+__,因为a=3__0,所以函数y有最___值,所以当
x=___时,y的最___值为__. a(x-h)2+khk(x+1)2>小-1小11(2)公式法:由二次函数y=ax2+bx+c的性质可得,当自变量
x=_____时,函数y最大(小)=________.如二次函数y=-2x2+8x+6,
因为a=-2__0,所以函数y有最___值,当x= =
=__时,y的最___值为 .<大2大________________________________2.实际问题中确定最值
【问题】某网店以每件60元的价格购进一批商品,若以单价80
元销售,每月可售出300件.调查表明:单价每上涨1元,该商品
每月的销售量就减少10件.
(1)请写出每月销售该商品的利润y(元)与单价上涨x(元)间的函
数关系式;
(2)单价定为多少元时,每月销售商品的利润最大?最大利润为
多少?【解题思路】(1)单价上涨x元后每件商品的售价为(_____)元,
每件商品的利润为________=(_____)元,每月的销售量为(____
______)件,每月销售该商品的利润y(元)与单价上涨x(元)间的
函数关系式为y=(_____)·(_________)=_________________.80+x80+x-6020+x300-10x20+x300-10x-10x2+100x+6 000(2)若设单价定为m元,则每件商品的利润为(_____)元,每月的
销售量为[300-_________]=(___________)件,每月销售该商品
的利润y(元)与单价m(元)间的函数关系式为y=(______)(________
____)=______________________.
即y=____(_____)2+______.
因为_____<0,所以当m=___时,y有最____值,______=______.
即单价定为___元时,每月销售商品的利润最大,最大利润为
______元. m-6010(m-80)1 100-10mm-601 100-10m-10 m2+1 700m-66 000-10m-856 250-1085y最大值6 250856 250大【点拨】准确理解实际问题中的等量关系是求最值的前提.
【预习思考】求二次函数最值的配方法与解一元二次方程的配
方法相同吗?
提示:相同. 求实际问题中的最值问题
【例】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,
求销售利润ω(元)与销售单价x(元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试
确定这种许愿瓶的销售单价,并求出此时的最大利润. 【规范解答】(1)y是x的一次函数,设y=kx+b,
图象过点(10,300),(12,240),
即可得 解得 ………………………2分
∴y=-30x+600.………………………………………………3分
当x=14时,y=180;当x=16时,y=120,
即点(14,180),(16,120)均在函数y=-30x+600的图象上,
∴y与x之间的函数关系式为y=-30x+600.…………………4分(2)ω=(x-6)(-30x+600)
=-30x2+780x-3 600,
即ω与x之间的函数关系式为
ω=-30x2+780x-3 600.………………………………………7分(3)由题意得6(-30x+600)≤900,解得x≥15,…………8分
ω=-30x2+780x-3 600的图象的对称轴为
x= =13,
∵a=-30<0,
∴抛物线开口向下,当x≥13时,ω随x增大而减小,
∴当x=13时,ω最大=1 470.
即以13元/个的价格销售这批许愿瓶可获得最大利润
1 470元.……………………………………………………10分【规律总结】
利用二次函数求解实际问题(如最大利润等)时,需注意事项
1.解答要全面,有时需要分类讨论(如涨价与降价、投入与产出
等).
2.分清每件的利润与销售量,理清价格与它们之间的关系.
3.自变量取值范围的确定,需保证实际问题有意义.
4.一般是利用二次函数的顶点坐标求最大值,但有时顶点坐标
不在取值范围内,注意画图象分析.【跟踪训练】
1.已知二次函数y=ax2+bx+c(a<0)的图象
如图所示,当-5≤x≤0时,下列说法正确的是( )
(A)有最小值-5,最大值0
(B)有最小值-3,最大值6
(C)有最小值0,最大值6
(D)有最小值2,最大值6【解析】选B.结合二次函数的图象,∵-5≤x≤0,
∴当x=-2时,函数有最大值,y最大=6;
当x=-5时,函数值最小,y最小=-3.2.某一型号飞机着陆后滑行的距离y(单位:m)
与滑行时间x(单位:s)之间的函数关系式是y=60x-1.5x2,该型
号飞机着陆后需滑行______m才能停下来.
【解析】根据题意得,飞机滑行停下了,求飞机的滑行距离,
即求函数y=60x-1.5x2的最大值,y=-1.5(x2-40x)=
-1.5(x-20)2+600≤600.
答案:6003.用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与
面积y(m2)满足函数关系y=-(x-12)2+144(0<x<24),则该矩形
面积的最大值为_______m2.
【解析】由函数关系y=-(x-12)2+144(0<x<24)可知,∵二次
函数的二次项系数即-1<0,∴当x=12时,y最大值=144.
答案:1444.如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A
开始沿AB向B以2 cm/s的速度移动,点Q从点B开始沿BC向C点以
1 cm/s的速度移动,如果P,Q分别从A,B同时出发,当△PBQ的
面积最大时,运动时间t为_____ s. 【解析】根据题意得三角形面积为:
由函数关系式可知
当t=2时,△PBQ的面积最大,为4 cm2.
答案:25.当k分别取-1,1,2时,函数y=(k-1)x2-
4x+5-k都有最大值吗?请写出你的判断,并说明理由;若有,请求
出最大值.
【解析】∵当开口向下时函数y=(k-1)x2-4x+5-k有最大值,
∴k-1<0,解得k<1.
∴当k=-1时,函数y=(k-1)x2-4x+5-k有最大值,
∴函数y=-2x2-4x+6=-2(x+1)2+8.
故最大值为8. 1.已知二次函数的图象(0≤x≤3)如图所.关
于该函数在所给自变量取值范围内,下列说法正确的是( )
(A)有最小值0,有最大值3
(B)有最小值-1,有最大值0
(C)有最小值-1,有最大值3
(D)有最小值-1,无最大值
【解析】选C.从图上观察知,当x=1时,有最小值-1,当x=3时,有最大值3.2.某广场有一喷水池,水从地面喷出,
如图,以水平地面为x轴,出水点为原
点,建立平面直角坐标系,水在空中
划出的曲线是抛物线y=-x2+4x(单位:
米)的一部分,则水喷出的最大高度是( )
(A)4米 (B)3米 (C)2米 (D)1米
【解析】选A.直接根据二次函数的顶点坐标公式计算即可,最
大高度为3.二次函数y=x2-2x+6的最小值是______.
【解析】y=x2-2x+6=x2-2x+1+5=(x-1)2+5,
可见二次函数y=x2-2x+6的最小值是5.
答案:5 4.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,
则当x=_______元时,一天出售该种手工艺品的总利润y最大.
【解析】总利润=单件产品利润×销售数量,因此y=x(8-x)
=-(x-4)2+16,当x=4时,总利润y有最大值16.
答案:45.星光中学课外活动小组准备围建一个矩形
生物苗圃园.其中一边靠墙,另外三边用长为30米的篱笆围
成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一
边的长为x米.(1)若平行于墙的一边的长为y米,直接写出y与x之间的函数关
系式及其自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,
并求出这个最大值;
(3)当这个苗圃园的面积不小于88平方米时,试结合函数图象,
直接写出x的取值范围.【解析】(1)y=30-2x(6≤x<15)
(2)设矩形苗圃园的面积为S,则S=xy=x(30-2x)=-2x2+30x,
∴S=-2(x-7.5)2+112.5.
由(1)知,6≤x<15,
∴当x=7.5时,S最大值=112.5,
即当矩形苗圃园垂直于墙的边长为7.5米时,这个苗圃园的面积
最大,最大值为112.5平方米.
(3)6≤x≤11
(1)配方法:y=ax2+bx+c化为y=_________的形式,当自变量x=__
时,函数y最大(小)=__.如二次函数y=3x2+6x+4可化为
y=3______+__,因为a=3__0,所以函数y有最___值,所以当
x=___时,y的最___值为__. a(x-h)2+khk(x+1)2>小-1小11(2)公式法:由二次函数y=ax2+bx+c的性质可得,当自变量
x=_____时,函数y最大(小)=________.如二次函数y=-2x2+8x+6,
因为a=-2__0,所以函数y有最___值,当x= =
=__时,y的最___值为 .<大2大________________________________2.实际问题中确定最值
【问题】某网店以每件60元的价格购进一批商品,若以单价80
元销售,每月可售出300件.调查表明:单价每上涨1元,该商品
每月的销售量就减少10件.
(1)请写出每月销售该商品的利润y(元)与单价上涨x(元)间的函
数关系式;
(2)单价定为多少元时,每月销售商品的利润最大?最大利润为
多少?【解题思路】(1)单价上涨x元后每件商品的售价为(_____)元,
每件商品的利润为________=(_____)元,每月的销售量为(____
______)件,每月销售该商品的利润y(元)与单价上涨x(元)间的
函数关系式为y=(_____)·(_________)=_________________.80+x80+x-6020+x300-10x20+x300-10x-10x2+100x+6 000(2)若设单价定为m元,则每件商品的利润为(_____)元,每月的
销售量为[300-_________]=(___________)件,每月销售该商品
的利润y(元)与单价m(元)间的函数关系式为y=(______)(________
____)=______________________.
即y=____(_____)2+______.
因为_____<0,所以当m=___时,y有最____值,______=______.
即单价定为___元时,每月销售商品的利润最大,最大利润为
______元. m-6010(m-80)1 100-10mm-601 100-10m-10 m2+1 700m-66 000-10m-856 250-1085y最大值6 250856 250大【点拨】准确理解实际问题中的等量关系是求最值的前提.
【预习思考】求二次函数最值的配方法与解一元二次方程的配
方法相同吗?
提示:相同. 求实际问题中的最值问题
【例】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,
求销售利润ω(元)与销售单价x(元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试
确定这种许愿瓶的销售单价,并求出此时的最大利润. 【规范解答】(1)y是x的一次函数,设y=kx+b,
图象过点(10,300),(12,240),
即可得 解得 ………………………2分
∴y=-30x+600.………………………………………………3分
当x=14时,y=180;当x=16时,y=120,
即点(14,180),(16,120)均在函数y=-30x+600的图象上,
∴y与x之间的函数关系式为y=-30x+600.…………………4分(2)ω=(x-6)(-30x+600)
=-30x2+780x-3 600,
即ω与x之间的函数关系式为
ω=-30x2+780x-3 600.………………………………………7分(3)由题意得6(-30x+600)≤900,解得x≥15,…………8分
ω=-30x2+780x-3 600的图象的对称轴为
x= =13,
∵a=-30<0,
∴抛物线开口向下,当x≥13时,ω随x增大而减小,
∴当x=13时,ω最大=1 470.
即以13元/个的价格销售这批许愿瓶可获得最大利润
1 470元.……………………………………………………10分【规律总结】
利用二次函数求解实际问题(如最大利润等)时,需注意事项
1.解答要全面,有时需要分类讨论(如涨价与降价、投入与产出
等).
2.分清每件的利润与销售量,理清价格与它们之间的关系.
3.自变量取值范围的确定,需保证实际问题有意义.
4.一般是利用二次函数的顶点坐标求最大值,但有时顶点坐标
不在取值范围内,注意画图象分析.【跟踪训练】
1.已知二次函数y=ax2+bx+c(a<0)的图象
如图所示,当-5≤x≤0时,下列说法正确的是( )
(A)有最小值-5,最大值0
(B)有最小值-3,最大值6
(C)有最小值0,最大值6
(D)有最小值2,最大值6【解析】选B.结合二次函数的图象,∵-5≤x≤0,
∴当x=-2时,函数有最大值,y最大=6;
当x=-5时,函数值最小,y最小=-3.2.某一型号飞机着陆后滑行的距离y(单位:m)
与滑行时间x(单位:s)之间的函数关系式是y=60x-1.5x2,该型
号飞机着陆后需滑行______m才能停下来.
【解析】根据题意得,飞机滑行停下了,求飞机的滑行距离,
即求函数y=60x-1.5x2的最大值,y=-1.5(x2-40x)=
-1.5(x-20)2+600≤600.
答案:6003.用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与
面积y(m2)满足函数关系y=-(x-12)2+144(0<x<24),则该矩形
面积的最大值为_______m2.
【解析】由函数关系y=-(x-12)2+144(0<x<24)可知,∵二次
函数的二次项系数即-1<0,∴当x=12时,y最大值=144.
答案:1444.如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A
开始沿AB向B以2 cm/s的速度移动,点Q从点B开始沿BC向C点以
1 cm/s的速度移动,如果P,Q分别从A,B同时出发,当△PBQ的
面积最大时,运动时间t为_____ s. 【解析】根据题意得三角形面积为:
由函数关系式可知
当t=2时,△PBQ的面积最大,为4 cm2.
答案:25.当k分别取-1,1,2时,函数y=(k-1)x2-
4x+5-k都有最大值吗?请写出你的判断,并说明理由;若有,请求
出最大值.
【解析】∵当开口向下时函数y=(k-1)x2-4x+5-k有最大值,
∴k-1<0,解得k<1.
∴当k=-1时,函数y=(k-1)x2-4x+5-k有最大值,
∴函数y=-2x2-4x+6=-2(x+1)2+8.
故最大值为8. 1.已知二次函数的图象(0≤x≤3)如图所.关
于该函数在所给自变量取值范围内,下列说法正确的是( )
(A)有最小值0,有最大值3
(B)有最小值-1,有最大值0
(C)有最小值-1,有最大值3
(D)有最小值-1,无最大值
【解析】选C.从图上观察知,当x=1时,有最小值-1,当x=3时,有最大值3.2.某广场有一喷水池,水从地面喷出,
如图,以水平地面为x轴,出水点为原
点,建立平面直角坐标系,水在空中
划出的曲线是抛物线y=-x2+4x(单位:
米)的一部分,则水喷出的最大高度是( )
(A)4米 (B)3米 (C)2米 (D)1米
【解析】选A.直接根据二次函数的顶点坐标公式计算即可,最
大高度为3.二次函数y=x2-2x+6的最小值是______.
【解析】y=x2-2x+6=x2-2x+1+5=(x-1)2+5,
可见二次函数y=x2-2x+6的最小值是5.
答案:5 4.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,
则当x=_______元时,一天出售该种手工艺品的总利润y最大.
【解析】总利润=单件产品利润×销售数量,因此y=x(8-x)
=-(x-4)2+16,当x=4时,总利润y有最大值16.
答案:45.星光中学课外活动小组准备围建一个矩形
生物苗圃园.其中一边靠墙,另外三边用长为30米的篱笆围
成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一
边的长为x米.(1)若平行于墙的一边的长为y米,直接写出y与x之间的函数关
系式及其自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,
并求出这个最大值;
(3)当这个苗圃园的面积不小于88平方米时,试结合函数图象,
直接写出x的取值范围.【解析】(1)y=30-2x(6≤x<15)
(2)设矩形苗圃园的面积为S,则S=xy=x(30-2x)=-2x2+30x,
∴S=-2(x-7.5)2+112.5.
由(1)知,6≤x<15,
∴当x=7.5时,S最大值=112.5,
即当矩形苗圃园垂直于墙的边长为7.5米时,这个苗圃园的面积
最大,最大值为112.5平方米.
(3)6≤x≤11
