浙教版八上数学2.1 图形的轴对称习题课件(26张)
文档属性
| 名称 | 浙教版八上数学2.1 图形的轴对称习题课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 747.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第1节 图形的轴对称
第2章 特殊三角形
浙教版 八年级上
答案显示
习题链接
D
D
C
D
B
C
A
8
B
答案显示
习题链接
10°
图略
图①有1条对称轴,图②有3条对称轴,图③有8条对称轴,图④有5条对称轴,图略
8
见习题
见习题
(1)证明见习题
(2)16
路线为A→C→D→B,作法见习题
1.【 2018?浙江湖州吴兴区期末】下列航空公司的标志中,是轴对称图形的是( )
D
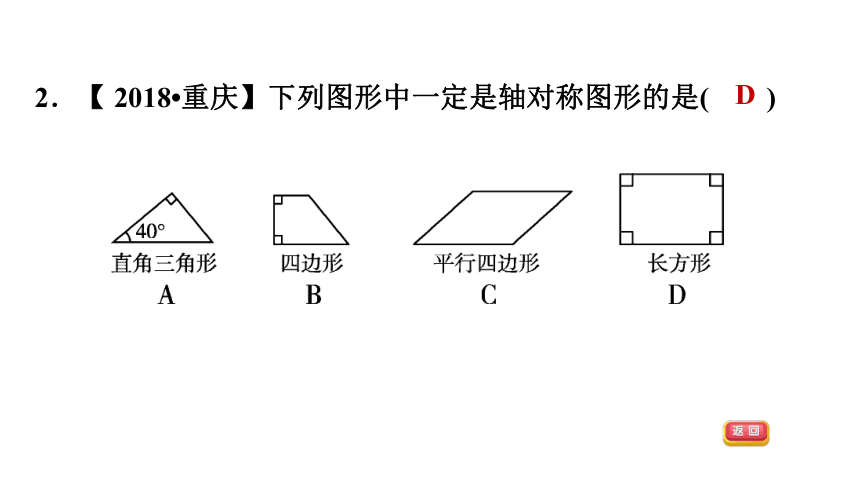
2.【 2018?重庆】下列图形中一定是轴对称图形的是( )
D
3.【中考·厦门】已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
C
【点拨】∵l=AB+BC+AC,∴BC=l-2AB=AB+BC+AC-2AB,∴AB=AC,∴△ABC的边BC上的中线所在的直线是△ABC的对称轴,故选C.
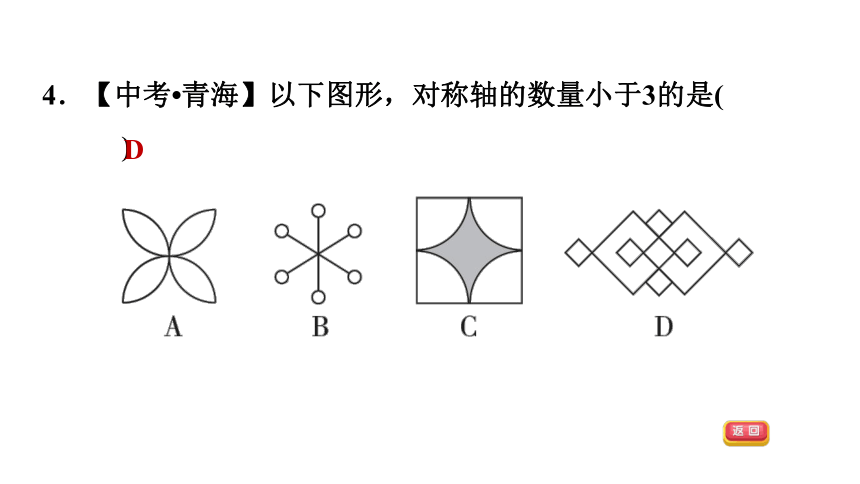
4.【中考?青海】以下图形,对称轴的数量小于3的是( )
D
5.【 中考?绍兴】如图是一个轴对称图形,其对称轴有( )
A.1条 B.2条
C.3条 D.4条
B
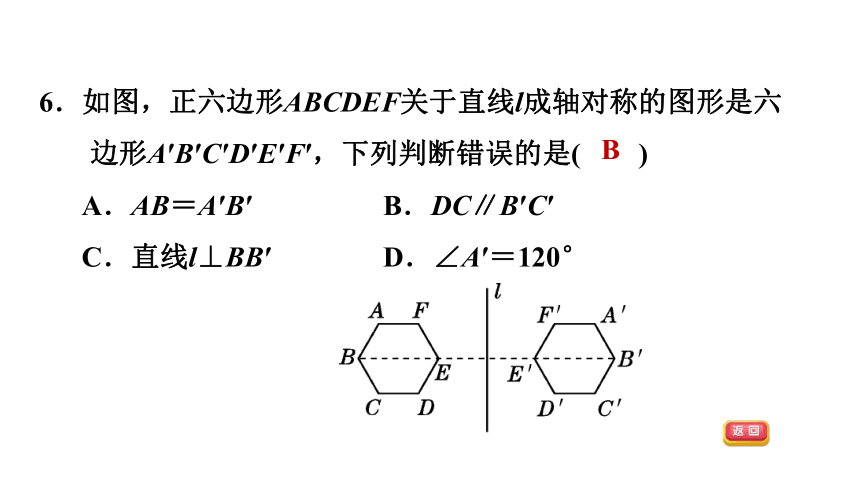
6.如图,正六边形ABCDEF关于直线l成轴对称的图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
A.AB=A′B′ B.DC∥B′C′
C.直线l⊥BB′ D.∠A′=120°
B
7.【 2017?遵义】把一张长方形纸片按如图①②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
C
8.【中考·聊城】如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
A.115° B.120°
C.130° D.140°
【点拨】∵把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,∴∠BFE=∠EFB′,∠B′=∠B=90°,∵∠2=40°,可得∠CFB′=50°,∵∠1+∠EFB′-∠CFB′=180°,∴∠1+∠1-50°=180°,∴∠1=115°,故选A.
9.如图,已知正方形的边长为4 cm,则图中阴影部分的面积为________cm2.
8
10.如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边 CB上的A′处,折痕为CD,则∠A′DB=________.
10°
11.补全如图所示的轴对称图形.(虚线为对称轴)
12.如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为________.
8
13.如图所示的图形分别有几条对称轴?分别画出它们的对称轴.
解:图①有1条对称轴,图②有3条对称轴,图③有8条对称轴,图④有5条对称轴.各图形的对称轴如图中的虚线所示.
14.如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F.试说明点E,F关于AD对称.
解:如图,连结EF交AD于点G,
因为AD平分∠BAC,所以∠EAD=∠FAD.
又因为∠AED=∠AFD=90°,AD=AD,
所以△ADE≌△ADF(AAS).
所以AE=AF.
又因为∠EAG=∠FAG,AG=AG,
所以△AEG≌△AFG (SAS).
所以EG=FG,∠AGE=∠AGF.
又因为∠AGE+∠AGF=180°,
所以∠AGE=∠AGF=90°.
所以AD垂直平分EF.
所以点E,F关于AD对称.
15.如图,A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两个蓄水池,并使所修的渠道最短,试在图中确定该抽水站所在的点.(保留作图痕迹)
解:如图,点P即为所求.
16.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
证明:由题易知∠GCF+∠FCE=90°,
∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
又由题易知,∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC.
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
17.如图,一牧马人从点A出发,到草地MN放牧,在傍晚回到帐篷B之前,先带马群到河边PQ去给马饮水.试问:牧马人应走哪条路线才能使整个放牧的路程最短,写出作法.
解:如图,作法如下:
(1)作点A关于直线MN的对称点A′,点B关于直线PQ的对称点B′.
(2)连结A′B′交MN于点C,交PQ于点D.
(3)连结AC,BD,则牧马人应走的路线为A→C→D→B.
第1节 图形的轴对称
第2章 特殊三角形
浙教版 八年级上
答案显示
习题链接
D
D
C
D
B
C
A
8
B
答案显示
习题链接
10°
图略
图①有1条对称轴,图②有3条对称轴,图③有8条对称轴,图④有5条对称轴,图略
8
见习题
见习题
(1)证明见习题
(2)16
路线为A→C→D→B,作法见习题
1.【 2018?浙江湖州吴兴区期末】下列航空公司的标志中,是轴对称图形的是( )
D
2.【 2018?重庆】下列图形中一定是轴对称图形的是( )
D
3.【中考·厦门】已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
C
【点拨】∵l=AB+BC+AC,∴BC=l-2AB=AB+BC+AC-2AB,∴AB=AC,∴△ABC的边BC上的中线所在的直线是△ABC的对称轴,故选C.
4.【中考?青海】以下图形,对称轴的数量小于3的是( )
D
5.【 中考?绍兴】如图是一个轴对称图形,其对称轴有( )
A.1条 B.2条
C.3条 D.4条
B
6.如图,正六边形ABCDEF关于直线l成轴对称的图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
A.AB=A′B′ B.DC∥B′C′
C.直线l⊥BB′ D.∠A′=120°
B
7.【 2017?遵义】把一张长方形纸片按如图①②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
C
8.【中考·聊城】如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
A.115° B.120°
C.130° D.140°
【点拨】∵把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,∴∠BFE=∠EFB′,∠B′=∠B=90°,∵∠2=40°,可得∠CFB′=50°,∵∠1+∠EFB′-∠CFB′=180°,∴∠1+∠1-50°=180°,∴∠1=115°,故选A.
9.如图,已知正方形的边长为4 cm,则图中阴影部分的面积为________cm2.
8
10.如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边 CB上的A′处,折痕为CD,则∠A′DB=________.
10°
11.补全如图所示的轴对称图形.(虚线为对称轴)
12.如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为________.
8
13.如图所示的图形分别有几条对称轴?分别画出它们的对称轴.
解:图①有1条对称轴,图②有3条对称轴,图③有8条对称轴,图④有5条对称轴.各图形的对称轴如图中的虚线所示.
14.如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F.试说明点E,F关于AD对称.
解:如图,连结EF交AD于点G,
因为AD平分∠BAC,所以∠EAD=∠FAD.
又因为∠AED=∠AFD=90°,AD=AD,
所以△ADE≌△ADF(AAS).
所以AE=AF.
又因为∠EAG=∠FAG,AG=AG,
所以△AEG≌△AFG (SAS).
所以EG=FG,∠AGE=∠AGF.
又因为∠AGE+∠AGF=180°,
所以∠AGE=∠AGF=90°.
所以AD垂直平分EF.
所以点E,F关于AD对称.
15.如图,A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两个蓄水池,并使所修的渠道最短,试在图中确定该抽水站所在的点.(保留作图痕迹)
解:如图,点P即为所求.
16.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
证明:由题易知∠GCF+∠FCE=90°,
∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
又由题易知,∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC.
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
17.如图,一牧马人从点A出发,到草地MN放牧,在傍晚回到帐篷B之前,先带马群到河边PQ去给马饮水.试问:牧马人应走哪条路线才能使整个放牧的路程最短,写出作法.
解:如图,作法如下:
(1)作点A关于直线MN的对称点A′,点B关于直线PQ的对称点B′.
(2)连结A′B′交MN于点C,交PQ于点D.
(3)连结AC,BD,则牧马人应走的路线为A→C→D→B.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
