浙教版八上数学2.4 等腰三角形的判定定理习题课件(30张)
文档属性
| 名称 | 浙教版八上数学2.4 等腰三角形的判定定理习题课件(30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 504.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
第4节 等腰三角形的判定定理
第2章 特殊三角形
浙教版 八年级上
答案显示
习题链接
D
D
C
C
A
C
①②③④
5
D
答案显示
习题链接
30°或75°或120°
30
(1)∠F=30°
(2)DF=4
等腰三角形,理由见习题
(1)证明见习题;
(2)∠BOC=100°
证明见习题
(1)①②和①③
(2)选①②,证明见习题
(1)证明见习题;
(2)解:BC=CE+AB
1.在△ABC中,不能判定是等腰三角形的是( )
A.∠A:∠B:∠C=1:1:3
B.a:b:c=2:2:3
C.∠B=50°,∠C=80°
D.2∠A=∠B+∠C
D
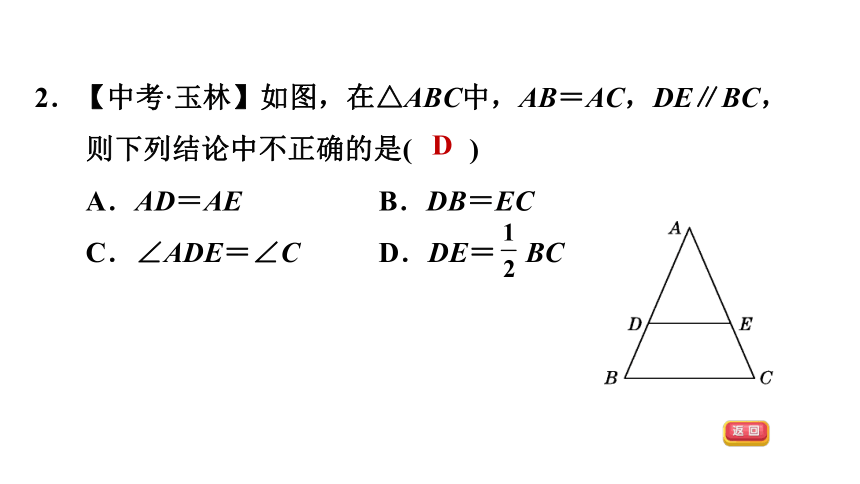
2.【中考·玉林】如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
A.AD=AE B.DB=EC
C.∠ADE=∠C D.DE= BC
D
3.如图,在△ABC中,BD平分∠ABC,ED∥BC,已知AB=3,AD=1,则△AED的周长为( )
A.2 B.3 C.4 D.5
C
【点拨】∵BD平分∠ABC,∴∠ABD=∠CBD.
∵ED∥BC,∴∠CBD=∠BDE.
∴∠ABD=∠BDE,∴BE=DE,
∴△AED的周长=AE+DE+AD=AE+BE+AD=AB+AD=3+1=4.
4.等腰三角形补充下列条件后,一定成为等边三角形的是( )
A.有两个角相等 B.有两个外角相等
C.有一个内角是60° D.有两边相等
C
5.如果一个三角形的一内角平分线垂直于对边,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
A
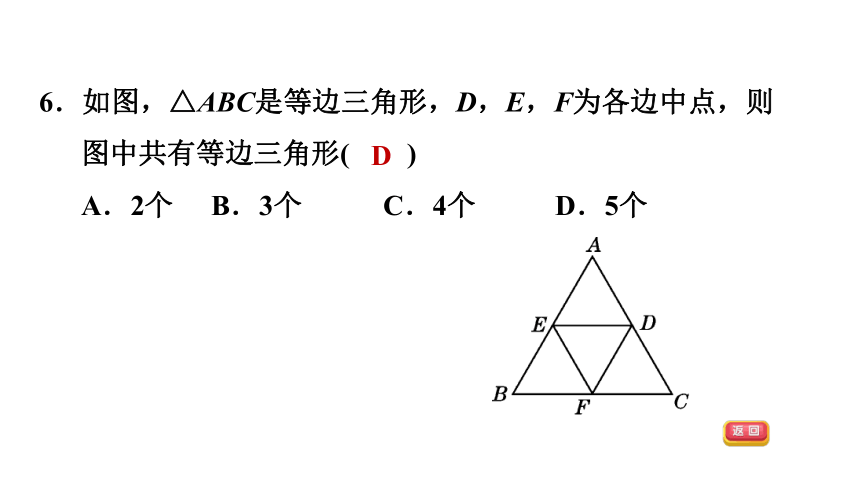
6.如图,△ABC是等边三角形,D,E,F为各边中点,则图中共有等边三角形( )
A.2个 B.3个 C.4个 D.5个
D
7.如图,在△ABC中,∠C=90°,∠A=30°,在直线AC上取一点P,使得△PAB是等腰三角形,则符合条件的点P有( )
A.2个 B.3个
C.4个 D.5个
C
8.下列三角形:
①有两个角等于60°的三角形;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有____________.(填序号)
①②③④
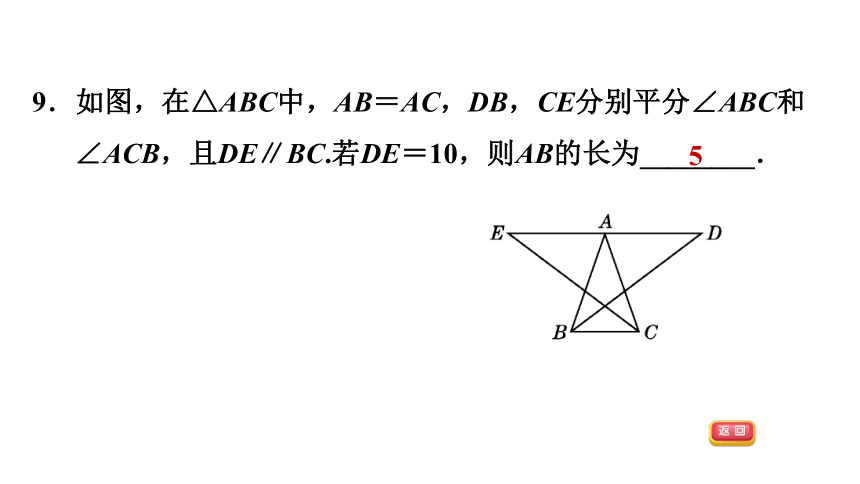
9.如图,在△ABC中,AB=AC,DB,CE分别平分∠ABC和∠ACB,且DE∥BC.若DE=10,则AB的长为________.
5
10.在△ABC中,∠A=30°,当∠B=_________________时,△ABC是等腰三角形.
30°或75°或120°
11.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北方向航行,10时到达B处,从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离是________海里.
30
12.【 2018·浙江宁波余姚期中】如图,已知AC⊥BC,AD⊥DB,AD=BC,那么请你判断阴影部分图形的形状,并说明理由.
解:等腰三角形.
理由如下: ∵AC⊥BC,AD⊥BD,∴∠C=∠D=90°.
又∵BC=AD,AB=BA,
∴△ACB≌△BDA.
∴∠CBA=∠DAB.
∴OB=OA(等角对等边).
∴阴影部分图形是等腰三角形.
13.【中考·温州】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
解:∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°.
∴∠F=90°-∠EDC=30°.
(2)若CD=2,求DF的长.
解:∵△ABC是等边三角形,∴∠ACB=60°,
又∵∠EDC=60°,∴△EDC是等边三角形.
∴∠DEC=60°,CE=DC=2.
∵∠DEF=90°,
∴∠CEF=90°-∠DEC=30°,∠F=90°-∠EDC=30°.
∴∠CEF=∠F,∴CF=CE=2. ∴DF=4.
14.【中考·常州】如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
证明:∵AB=AC,∴∠ABC=∠ACB,
∵BD,CE是△ABC的两条高线,
∴∠BDC=∠BEC=90°,即∠DBC+∠DCB=∠ECB+∠CBE=90°.
∴∠DBC=∠ECB,∴OB=OC.
(2)若∠ABC=50°,求∠BOC的度数.
解:∵∠ABC=50°,AB=AC,
∴∠A=180°-2×50°=80°,
∵∠ABD+∠A=90°,∴∠ABD=10°,
∴∠BOC=∠ABD+∠BEO=100°.
15.如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF.求证:DE=DF.
【点拨】本题既利用了等腰三角形的性质,又利用了
等腰三角形的判定.同一个题中同时用到等腰三角形的
性质定理和判定定理时,应注意它们的区别与联系.另外本题还可以过点F作FH∥AB交BC的延长线于点H,由已知条件推得△DBE≌△DHF.
16.【中考·襄阳】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
解:①②和①③
(2)请选择(1)中的一种情形,写出证明过程.
解:选①②,证明如下:
在△BOE和△COD中,
∵∠EBO=∠DCO,∠EOB=∠DOC,BE=CD,
∴△BOE≌△COD,∴BO=CO,∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,
∴AB=AC,即△ABC是等腰三角形.
17.如图,已知在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.
(1)求证:BC=BE+AE;
证明:在BC上截取BD=BE,连结DE(如图①).
∵AB=AC,∠BAC=100°,
∴∠ABC=∠C=(180°-100°)÷2=40°.
∵BE平分∠ABC,
∴∠CBE=∠ABE=20°.
①
又∵BD=BE,∴∠BDE=∠BED=(180°-20°)÷2=80°.
又∵∠BDE=∠C+∠CED,∠C=40°,
∴∠CED=40°=∠C,∴DE=DC.
过点E作EM⊥BA交BA的延长线于点M,EN⊥BC于点N.
∵BE平分∠ABC,
∴EM=EN.
∵∠BAC=100°,
∴∠CAM=180°-100°=80°.
(2)探究:若∠A=108°,那么BC等于哪两条线段长的和呢?试说明理由.
解:BC=CE+AB.理由如下.
在CB上截取CP=CE,连结PE(如图②).
∵AB=AC,∠A=108°,
∴∠ABC=∠C=(180°-108°)÷2=36°.
②
∴∠CPE=(180°-36°)÷2=72°.
∴∠BPE=180°-72°=108°. ∴∠BPE=∠A.
∵BE平分∠ABC,∴∠ABE=∠PBE.
第4节 等腰三角形的判定定理
第2章 特殊三角形
浙教版 八年级上
答案显示
习题链接
D
D
C
C
A
C
①②③④
5
D
答案显示
习题链接
30°或75°或120°
30
(1)∠F=30°
(2)DF=4
等腰三角形,理由见习题
(1)证明见习题;
(2)∠BOC=100°
证明见习题
(1)①②和①③
(2)选①②,证明见习题
(1)证明见习题;
(2)解:BC=CE+AB
1.在△ABC中,不能判定是等腰三角形的是( )
A.∠A:∠B:∠C=1:1:3
B.a:b:c=2:2:3
C.∠B=50°,∠C=80°
D.2∠A=∠B+∠C
D
2.【中考·玉林】如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
A.AD=AE B.DB=EC
C.∠ADE=∠C D.DE= BC
D
3.如图,在△ABC中,BD平分∠ABC,ED∥BC,已知AB=3,AD=1,则△AED的周长为( )
A.2 B.3 C.4 D.5
C
【点拨】∵BD平分∠ABC,∴∠ABD=∠CBD.
∵ED∥BC,∴∠CBD=∠BDE.
∴∠ABD=∠BDE,∴BE=DE,
∴△AED的周长=AE+DE+AD=AE+BE+AD=AB+AD=3+1=4.
4.等腰三角形补充下列条件后,一定成为等边三角形的是( )
A.有两个角相等 B.有两个外角相等
C.有一个内角是60° D.有两边相等
C
5.如果一个三角形的一内角平分线垂直于对边,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
A
6.如图,△ABC是等边三角形,D,E,F为各边中点,则图中共有等边三角形( )
A.2个 B.3个 C.4个 D.5个
D
7.如图,在△ABC中,∠C=90°,∠A=30°,在直线AC上取一点P,使得△PAB是等腰三角形,则符合条件的点P有( )
A.2个 B.3个
C.4个 D.5个
C
8.下列三角形:
①有两个角等于60°的三角形;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有____________.(填序号)
①②③④
9.如图,在△ABC中,AB=AC,DB,CE分别平分∠ABC和∠ACB,且DE∥BC.若DE=10,则AB的长为________.
5
10.在△ABC中,∠A=30°,当∠B=_________________时,△ABC是等腰三角形.
30°或75°或120°
11.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北方向航行,10时到达B处,从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离是________海里.
30
12.【 2018·浙江宁波余姚期中】如图,已知AC⊥BC,AD⊥DB,AD=BC,那么请你判断阴影部分图形的形状,并说明理由.
解:等腰三角形.
理由如下: ∵AC⊥BC,AD⊥BD,∴∠C=∠D=90°.
又∵BC=AD,AB=BA,
∴△ACB≌△BDA.
∴∠CBA=∠DAB.
∴OB=OA(等角对等边).
∴阴影部分图形是等腰三角形.
13.【中考·温州】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
解:∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°.
∴∠F=90°-∠EDC=30°.
(2)若CD=2,求DF的长.
解:∵△ABC是等边三角形,∴∠ACB=60°,
又∵∠EDC=60°,∴△EDC是等边三角形.
∴∠DEC=60°,CE=DC=2.
∵∠DEF=90°,
∴∠CEF=90°-∠DEC=30°,∠F=90°-∠EDC=30°.
∴∠CEF=∠F,∴CF=CE=2. ∴DF=4.
14.【中考·常州】如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
证明:∵AB=AC,∴∠ABC=∠ACB,
∵BD,CE是△ABC的两条高线,
∴∠BDC=∠BEC=90°,即∠DBC+∠DCB=∠ECB+∠CBE=90°.
∴∠DBC=∠ECB,∴OB=OC.
(2)若∠ABC=50°,求∠BOC的度数.
解:∵∠ABC=50°,AB=AC,
∴∠A=180°-2×50°=80°,
∵∠ABD+∠A=90°,∴∠ABD=10°,
∴∠BOC=∠ABD+∠BEO=100°.
15.如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF.求证:DE=DF.
【点拨】本题既利用了等腰三角形的性质,又利用了
等腰三角形的判定.同一个题中同时用到等腰三角形的
性质定理和判定定理时,应注意它们的区别与联系.另外本题还可以过点F作FH∥AB交BC的延长线于点H,由已知条件推得△DBE≌△DHF.
16.【中考·襄阳】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
解:①②和①③
(2)请选择(1)中的一种情形,写出证明过程.
解:选①②,证明如下:
在△BOE和△COD中,
∵∠EBO=∠DCO,∠EOB=∠DOC,BE=CD,
∴△BOE≌△COD,∴BO=CO,∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,
∴AB=AC,即△ABC是等腰三角形.
17.如图,已知在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.
(1)求证:BC=BE+AE;
证明:在BC上截取BD=BE,连结DE(如图①).
∵AB=AC,∠BAC=100°,
∴∠ABC=∠C=(180°-100°)÷2=40°.
∵BE平分∠ABC,
∴∠CBE=∠ABE=20°.
①
又∵BD=BE,∴∠BDE=∠BED=(180°-20°)÷2=80°.
又∵∠BDE=∠C+∠CED,∠C=40°,
∴∠CED=40°=∠C,∴DE=DC.
过点E作EM⊥BA交BA的延长线于点M,EN⊥BC于点N.
∵BE平分∠ABC,
∴EM=EN.
∵∠BAC=100°,
∴∠CAM=180°-100°=80°.
(2)探究:若∠A=108°,那么BC等于哪两条线段长的和呢?试说明理由.
解:BC=CE+AB.理由如下.
在CB上截取CP=CE,连结PE(如图②).
∵AB=AC,∠A=108°,
∴∠ABC=∠C=(180°-108°)÷2=36°.
②
∴∠CPE=(180°-36°)÷2=72°.
∴∠BPE=180°-72°=108°. ∴∠BPE=∠A.
∵BE平分∠ABC,∴∠ABE=∠PBE.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
