浙教版八上数学第2章特殊三角形全章热门考点整合课件(26张)
文档属性
| 名称 | 浙教版八上数学第2章特殊三角形全章热门考点整合课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
全章热门考点整合
第2章 特殊三角形
浙教版 八年级上
答案显示
习题链接
D
一个数是自然数;这个数是有理数;一个数是有理数;这个数是自然数
B
证明见习题
48
证明见习题
证明见习题
证明见习题
C
答案显示
习题链接
(1)证明见习题
(2)证明见习题
(3)成立
15m
A
6或6.5
∠A=45°
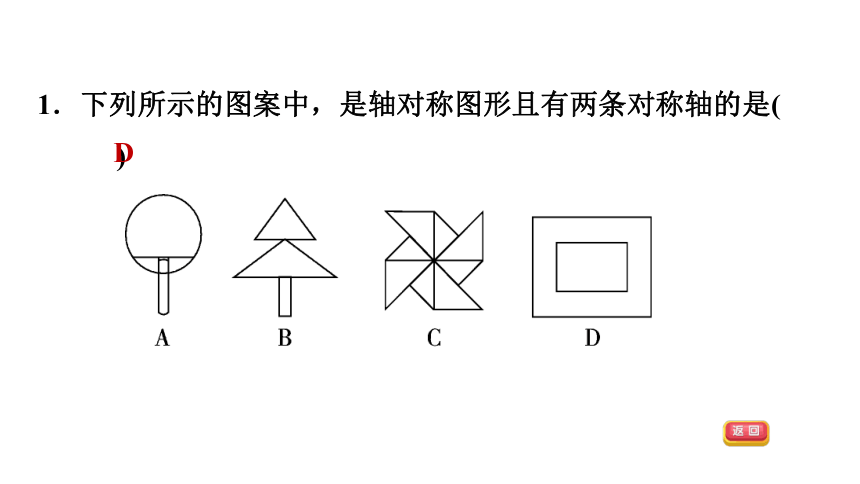
1.下列所示的图案中,是轴对称图形且有两条对称轴的是( )
D
2.命题“自然数必为有理数”的条件是____________________,结论是____________________,它的逆命题的条件是______________________,结论是__________________.
一个数是自然数
这个数是有理数
一个数是有理数
这个数是自然数
3.如图,△ABC和△AB′C′关于直线l对称,下列结论:
①△ABC≌△AB′C′;
②∠BAC′=∠B′AC;
③直线l垂直平分CC′;
④直线BC和B′C′的交点不一定在直线l上.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
B
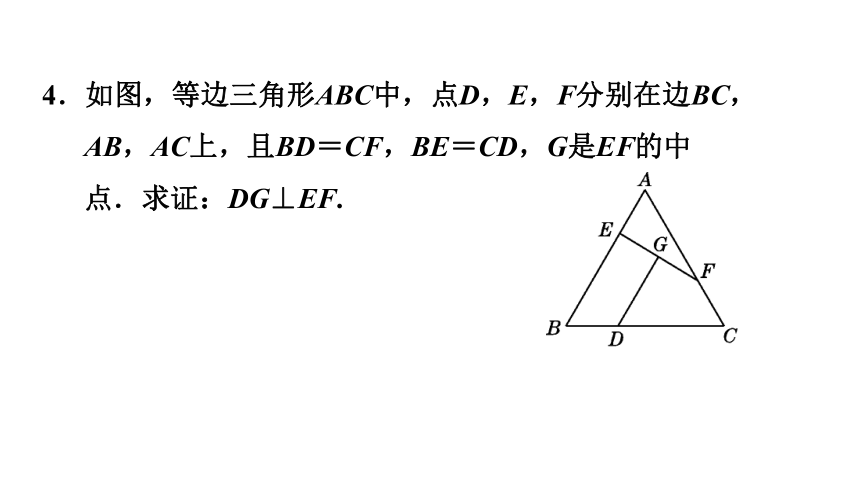
4.如图,等边三角形ABC中,点D,E,F分别在边BC,AB,AC上,且BD=CF,BE=CD,G是EF的中点.求证:DG⊥EF.
5.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,若c-b=2,a=14,则b=________.
48
【点拨】∵c-b=2,∴c=b+2.
∵∠C=90°,∴a2+b2=c2,
即142+b2=(b+2)2,解得b=48.
6.等腰三角形补充下列条件后,仍不一定成为等边三角形的是( )
A.有一个内角是60° B.有一个外角是120°
C.有两个角相等 D.腰与底边相等
C
7.如图,AF平分∠BAC,P是AF上任意一点,过P向AB,AC作垂线PD,PE,垂足分别为D,E,连结DE.求证:AF垂直平分DE.
证明:∵AF平分∠BAC,PD⊥AB,PE⊥AC(已知),
∴PD=PE,∴点P在DE的垂直平分线上.
8.如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB,AC上的动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
证明:连结AD,∵△ABC是等腰直角三角形,D是BC的中点,
∴AD⊥BC,AD=BD=DC,
易得∠DAQ=∠B,
又∵BP=AQ,
∴△BPD≌△AQD,∴PD=QD,∠ADQ=∠BDP,
∵∠BDP+∠ADP=90°,
∴∠ADQ+∠ADP=∠PDQ=90°,
∴△PDQ是等腰直角三角形.
9.如图,在△ABC中,D是BC边上一点,连结AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.
求证:AD是△ABC的中线.
证明:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
又∵∠BDE=∠CDF,BE=CF,
∴△DBE≌△DCF,∴BD=CD.
∴D是BC的中点,
即AD是△ABC的中线.
10.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且AB=AC.
(1)如图①,若点O在边BC上,求证:OB=OC.
证明:过点O分别作OE⊥AB于点E,OF⊥AC于点F,连结AO.
由题意知,OE=OF,
∴点O在∠BAC的平分线上,即AO为∠BAC的平分线.
又∵AB=AC,∴OB=OC.
(2)如图②,若点O在△ABC的内部,求证:OB=OC.
证明:如图①,过点O分别作OE⊥AB于点E,OF⊥AC于点F,连结AO并延长交BC于点D.
由题意知OE=OF.
∴点O在∠BAC的平分线上,即AD平分∠BAC,
又∵AB=AC,∴AD⊥BC,BD=DC.
即AD垂直平分BC.∴OB=OC.
(3)若点O在△ABC的外部,OB=OC成立吗?请画图表示并证明.
11.如图,在一棵大树的某一高处B点有两只猴子,其中一只胆小的猴子爬下树后走向离树20 m处的池塘D处,而另一只猴子胆子比较大,继续向上爬了5 m,爬到树顶A后直扑向池塘D处(设它从树顶到池塘经过的是一条直线),如果两只猴子所经过的路程相等,问这棵树有多高.
解:如图,AB=5 m,CD=20 m,AC为树高.
由题意设AD=x m,由AB+AD=BC+CD,
易得AC=(x-10)m.
由勾股定理得,AD2=AC2+CD2,
即x2=(x-10)2+202,解得x=25.
所以树高为x-10=15(m).
12.【 2018·浙江湖州吴兴区期末】已知直角三角形的两条边长分别是5和12,则斜边上的中线的长度为____________.
6或6.5
【答案】A
14.如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,求∠A的度数.
【点拨】本题运用了方程思想.题中含有4个等腰三角形,若反复运用“等边对等角”和三角形外角的性质,比较复杂且易出错,而用列方程的方法可使问题变得简单明了.
解:设∠ABD的度数为x.
∵AD=DE=EB,∴∠A=∠AED=2∠ABD=2x.
∵BC=BD,∴∠C=∠BDC=∠ABD+∠A=3x.
∵AB=AC,∴∠ABC=∠C=3x.
∴∠A+∠C+∠ABC=8x=180°.
∴x=22.5°.
∴∠A=2x=45°.
全章热门考点整合
第2章 特殊三角形
浙教版 八年级上
答案显示
习题链接
D
一个数是自然数;这个数是有理数;一个数是有理数;这个数是自然数
B
证明见习题
48
证明见习题
证明见习题
证明见习题
C
答案显示
习题链接
(1)证明见习题
(2)证明见习题
(3)成立
15m
A
6或6.5
∠A=45°
1.下列所示的图案中,是轴对称图形且有两条对称轴的是( )
D
2.命题“自然数必为有理数”的条件是____________________,结论是____________________,它的逆命题的条件是______________________,结论是__________________.
一个数是自然数
这个数是有理数
一个数是有理数
这个数是自然数
3.如图,△ABC和△AB′C′关于直线l对称,下列结论:
①△ABC≌△AB′C′;
②∠BAC′=∠B′AC;
③直线l垂直平分CC′;
④直线BC和B′C′的交点不一定在直线l上.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
B
4.如图,等边三角形ABC中,点D,E,F分别在边BC,AB,AC上,且BD=CF,BE=CD,G是EF的中点.求证:DG⊥EF.
5.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,若c-b=2,a=14,则b=________.
48
【点拨】∵c-b=2,∴c=b+2.
∵∠C=90°,∴a2+b2=c2,
即142+b2=(b+2)2,解得b=48.
6.等腰三角形补充下列条件后,仍不一定成为等边三角形的是( )
A.有一个内角是60° B.有一个外角是120°
C.有两个角相等 D.腰与底边相等
C
7.如图,AF平分∠BAC,P是AF上任意一点,过P向AB,AC作垂线PD,PE,垂足分别为D,E,连结DE.求证:AF垂直平分DE.
证明:∵AF平分∠BAC,PD⊥AB,PE⊥AC(已知),
∴PD=PE,∴点P在DE的垂直平分线上.
8.如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB,AC上的动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
证明:连结AD,∵△ABC是等腰直角三角形,D是BC的中点,
∴AD⊥BC,AD=BD=DC,
易得∠DAQ=∠B,
又∵BP=AQ,
∴△BPD≌△AQD,∴PD=QD,∠ADQ=∠BDP,
∵∠BDP+∠ADP=90°,
∴∠ADQ+∠ADP=∠PDQ=90°,
∴△PDQ是等腰直角三角形.
9.如图,在△ABC中,D是BC边上一点,连结AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.
求证:AD是△ABC的中线.
证明:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
又∵∠BDE=∠CDF,BE=CF,
∴△DBE≌△DCF,∴BD=CD.
∴D是BC的中点,
即AD是△ABC的中线.
10.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且AB=AC.
(1)如图①,若点O在边BC上,求证:OB=OC.
证明:过点O分别作OE⊥AB于点E,OF⊥AC于点F,连结AO.
由题意知,OE=OF,
∴点O在∠BAC的平分线上,即AO为∠BAC的平分线.
又∵AB=AC,∴OB=OC.
(2)如图②,若点O在△ABC的内部,求证:OB=OC.
证明:如图①,过点O分别作OE⊥AB于点E,OF⊥AC于点F,连结AO并延长交BC于点D.
由题意知OE=OF.
∴点O在∠BAC的平分线上,即AD平分∠BAC,
又∵AB=AC,∴AD⊥BC,BD=DC.
即AD垂直平分BC.∴OB=OC.
(3)若点O在△ABC的外部,OB=OC成立吗?请画图表示并证明.
11.如图,在一棵大树的某一高处B点有两只猴子,其中一只胆小的猴子爬下树后走向离树20 m处的池塘D处,而另一只猴子胆子比较大,继续向上爬了5 m,爬到树顶A后直扑向池塘D处(设它从树顶到池塘经过的是一条直线),如果两只猴子所经过的路程相等,问这棵树有多高.
解:如图,AB=5 m,CD=20 m,AC为树高.
由题意设AD=x m,由AB+AD=BC+CD,
易得AC=(x-10)m.
由勾股定理得,AD2=AC2+CD2,
即x2=(x-10)2+202,解得x=25.
所以树高为x-10=15(m).
12.【 2018·浙江湖州吴兴区期末】已知直角三角形的两条边长分别是5和12,则斜边上的中线的长度为____________.
6或6.5
【答案】A
14.如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,求∠A的度数.
【点拨】本题运用了方程思想.题中含有4个等腰三角形,若反复运用“等边对等角”和三角形外角的性质,比较复杂且易出错,而用列方程的方法可使问题变得简单明了.
解:设∠ABD的度数为x.
∵AD=DE=EB,∴∠A=∠AED=2∠ABD=2x.
∵BC=BD,∴∠C=∠BDC=∠ABD+∠A=3x.
∵AB=AC,∴∠ABC=∠C=3x.
∴∠A+∠C+∠ABC=8x=180°.
∴x=22.5°.
∴∠A=2x=45°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
