浙教版八上数学第2章特殊三角形的探究性问题课件(28张)
文档属性
| 名称 | 浙教版八上数学第2章特殊三角形的探究性问题课件(28张) |  | |
| 格式 | zip | ||
| 文件大小 | 501.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 11:02:26 | ||
图片预览







文档简介
(共28张PPT)
特殊三角形的探究性问题
第1章 三角形的初步认识
浙教版 八年级上
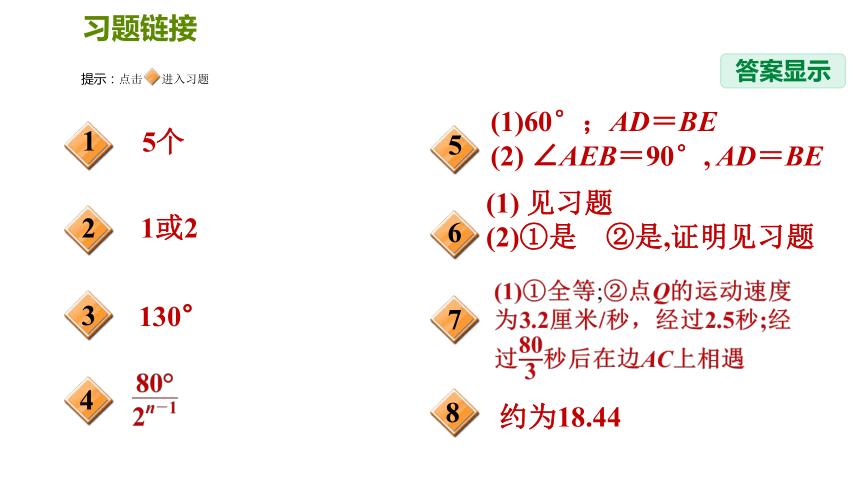
答案显示
习题链接
130°
5个
1或2
约为18.44
(1)60°;AD=BE
(2) ∠AEB=90°, AD=BE
(1) 见习题
(2)①是 ②是,证明见习题
【例】在△ABC中,AB=AC,∠B=50°,点D是AB上的一点,点P是BC上的一点(不与B,C重合),∠PAC=∠BPD,若△APD是等腰三角形,求∠PAD的度数.
【解题秘方】本题考查的是等腰三角形的性质定理1.根据△APD是等腰三角形分三种情况进行讨论.
解:∵AB=AC,∴∠C=∠B=50°.
∵∠APB=∠BPD+∠APD=∠PAC+∠C,∠PAC=∠BPD,∴∠APD=∠C=50°.
由△APD是等腰三角形,可分三种情况讨论:
①若AD=AP,则∠ADP=∠APD=50°,
∵∠B=50°,∠ADP>∠B,
∴∠ADP=50°不成立,∴AD≠AP;
②若AD=DP,则∠PAD=∠APD=50°;
③若PD=AP,则∠PAD=∠PDA=(180°-50°)÷2=65°.
综上所述,∠PAD的度数为50°或65°.
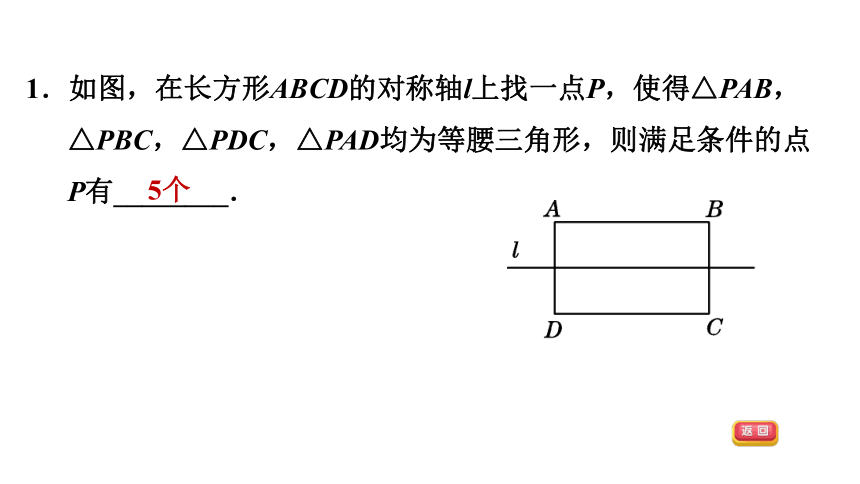
1.如图,在长方形ABCD的对称轴l上找一点P,使得△PAB,△PBC,△PDC,△PAD均为等腰三角形,则满足条件的点P有________.
5个
2.如图,已知△ABC是边长为3 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P,Q两点停止.设它们运动的时间为t s当t=________时,△PBQ是直角三角形.
1或2
3.如图,四边形ABCD中,∠BAD=115°,∠B=∠D=90°,M,N分别为BC,CD上的一个动点.当△AMN的周长最小时,∠AMN+∠ANM的度数为________.
【点拨】如图,作A关于BC和CD的对称点A′,A″,连结A′A″,交BC于M,交CD于N,则线段A′A″的长为△AMN的周长的最小值.
易知∠A′=∠BAM,∠A″=∠DAN,
∵∠BAD=115°,∴∠A′+∠A″=180°-115°=65°.
∴∠BAM+∠DAN=65°.∴∠MAN=115°-65°=50°.
∴∠AMN+∠ANM=180°-50°=130°.
4.【 中考·贵阳】如图,在第1个△ABA1中,∠B=20°,AB=A1B.在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D……按此作法进行下去,第n个三角形以An为顶点的内角的度数为________.
5.如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE,且点A,D,E在同一直线上,连结BE.
(1)若∠ACB=60°,如图①,则∠AEB的度数为__________;线段AD,BE之间的数量关系是__________.
60°
AD=BE
(2)若∠ACB=∠DCE=90°,如图②,求∠AEB的度数,并判断AD,BE之间的数量关系.
∴△ACD≌△BCE.
∴∠CDA=∠CEB,AD=BE.
易得△CDE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∴∠CEB=∠CDA=180°-45°=135°.
∴∠AEB=135°-45°=90°.
6.(1)如图①,点M,N分别在等边△ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.试说明:∠BQM=60°.
解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
∵BM=CN,∴△ABM≌△BCN(SAS).
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM=∠ABQ+∠CBN=60°.
(2)①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动BC,CA的延长线上,如图②,是否仍能得到∠BQM=60°?
请你进行判断,在下列横线上填写“是”或“否”:
①________;②________.并对②给出证明.
是
是
证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∴∠BAN=∠ACM=120°,
又CN=BM,∴AN=CM.
∴△ANB≌△CMA.∴∠N=∠M.
∵∠NAQ=∠MAC,
∴∠BQM=∠ACB=60°.
7.如图,在△ABC中,AB=AC=16厘米,BC=10厘米,点D为AB的中点.
(1)如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
解:∵AB=AC=16厘米,点D为AB的中点,
∴BD=8厘米,∠B=∠C,
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
解:∵AB=AC=16厘米,点D为AB的中点,
∴BD=8厘米,∠B=∠C,
设当点Q的运动速度为a厘米/秒时,经过t秒,能够使△BPD与△CQP全等,
∵点Q的运动速度与点P的运动速度不相等,
∴BP和CQ不是对应边,则BD=CQ,BP=CP,
∴2t=10-2t,解得t=2.5,
∵BD=CQ,∴8=2.5a,
解得a=3.2,即当点Q的运动速度为3.2厘米/秒时,经过2.5秒,能够使△BPD与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
8.有一个长方体纸盒,如图所示,小明所在数学小组研究从长方体的底面A点沿长方体表面到与A点相对的B点的最短距离.若长方体的长为12,宽为9,高为5,请你帮助该小组求出在长方体表面上由A点到B点的最短距离.(参考数据:21.592≈466,19.242≈370,18.442≈340)
解:将四边形ACDF与四边形FDBG展开在同一平面上,如图①,连结AB.
在直角三角形ACB中,根据勾股定理,得AB2=AC2+BC2=122+(9+5)2=340.
将四边形AHGF与四边形FDBG展开在同一平面上,如图②,连结AB.
在直角三角形ABD中,根据勾股定理,得AB2=AD2+DB2=(12+5)2+92=370.
将四边形ACDF与四边形DCEB展开在同一平面上,如图③,连结AB.
在直角三角形AEB中,根据勾股定理,得AB2=AE2+EB2=(12+9)2+52=466.
因为340<370<466,
所以在长方体表面上由A点到B点的最短距离是如图①的情况,
此时AB≈18.44.
所以在长方体表面上由A点到B点的最短距离约为18.44.
特殊三角形的探究性问题
第1章 三角形的初步认识
浙教版 八年级上
答案显示
习题链接
130°
5个
1或2
约为18.44
(1)60°;AD=BE
(2) ∠AEB=90°, AD=BE
(1) 见习题
(2)①是 ②是,证明见习题
【例】在△ABC中,AB=AC,∠B=50°,点D是AB上的一点,点P是BC上的一点(不与B,C重合),∠PAC=∠BPD,若△APD是等腰三角形,求∠PAD的度数.
【解题秘方】本题考查的是等腰三角形的性质定理1.根据△APD是等腰三角形分三种情况进行讨论.
解:∵AB=AC,∴∠C=∠B=50°.
∵∠APB=∠BPD+∠APD=∠PAC+∠C,∠PAC=∠BPD,∴∠APD=∠C=50°.
由△APD是等腰三角形,可分三种情况讨论:
①若AD=AP,则∠ADP=∠APD=50°,
∵∠B=50°,∠ADP>∠B,
∴∠ADP=50°不成立,∴AD≠AP;
②若AD=DP,则∠PAD=∠APD=50°;
③若PD=AP,则∠PAD=∠PDA=(180°-50°)÷2=65°.
综上所述,∠PAD的度数为50°或65°.
1.如图,在长方形ABCD的对称轴l上找一点P,使得△PAB,△PBC,△PDC,△PAD均为等腰三角形,则满足条件的点P有________.
5个
2.如图,已知△ABC是边长为3 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P,Q两点停止.设它们运动的时间为t s当t=________时,△PBQ是直角三角形.
1或2
3.如图,四边形ABCD中,∠BAD=115°,∠B=∠D=90°,M,N分别为BC,CD上的一个动点.当△AMN的周长最小时,∠AMN+∠ANM的度数为________.
【点拨】如图,作A关于BC和CD的对称点A′,A″,连结A′A″,交BC于M,交CD于N,则线段A′A″的长为△AMN的周长的最小值.
易知∠A′=∠BAM,∠A″=∠DAN,
∵∠BAD=115°,∴∠A′+∠A″=180°-115°=65°.
∴∠BAM+∠DAN=65°.∴∠MAN=115°-65°=50°.
∴∠AMN+∠ANM=180°-50°=130°.
4.【 中考·贵阳】如图,在第1个△ABA1中,∠B=20°,AB=A1B.在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D……按此作法进行下去,第n个三角形以An为顶点的内角的度数为________.
5.如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE,且点A,D,E在同一直线上,连结BE.
(1)若∠ACB=60°,如图①,则∠AEB的度数为__________;线段AD,BE之间的数量关系是__________.
60°
AD=BE
(2)若∠ACB=∠DCE=90°,如图②,求∠AEB的度数,并判断AD,BE之间的数量关系.
∴△ACD≌△BCE.
∴∠CDA=∠CEB,AD=BE.
易得△CDE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∴∠CEB=∠CDA=180°-45°=135°.
∴∠AEB=135°-45°=90°.
6.(1)如图①,点M,N分别在等边△ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.试说明:∠BQM=60°.
解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
∵BM=CN,∴△ABM≌△BCN(SAS).
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM=∠ABQ+∠CBN=60°.
(2)①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动BC,CA的延长线上,如图②,是否仍能得到∠BQM=60°?
请你进行判断,在下列横线上填写“是”或“否”:
①________;②________.并对②给出证明.
是
是
证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∴∠BAN=∠ACM=120°,
又CN=BM,∴AN=CM.
∴△ANB≌△CMA.∴∠N=∠M.
∵∠NAQ=∠MAC,
∴∠BQM=∠ACB=60°.
7.如图,在△ABC中,AB=AC=16厘米,BC=10厘米,点D为AB的中点.
(1)如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
解:∵AB=AC=16厘米,点D为AB的中点,
∴BD=8厘米,∠B=∠C,
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
解:∵AB=AC=16厘米,点D为AB的中点,
∴BD=8厘米,∠B=∠C,
设当点Q的运动速度为a厘米/秒时,经过t秒,能够使△BPD与△CQP全等,
∵点Q的运动速度与点P的运动速度不相等,
∴BP和CQ不是对应边,则BD=CQ,BP=CP,
∴2t=10-2t,解得t=2.5,
∵BD=CQ,∴8=2.5a,
解得a=3.2,即当点Q的运动速度为3.2厘米/秒时,经过2.5秒,能够使△BPD与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
8.有一个长方体纸盒,如图所示,小明所在数学小组研究从长方体的底面A点沿长方体表面到与A点相对的B点的最短距离.若长方体的长为12,宽为9,高为5,请你帮助该小组求出在长方体表面上由A点到B点的最短距离.(参考数据:21.592≈466,19.242≈370,18.442≈340)
解:将四边形ACDF与四边形FDBG展开在同一平面上,如图①,连结AB.
在直角三角形ACB中,根据勾股定理,得AB2=AC2+BC2=122+(9+5)2=340.
将四边形AHGF与四边形FDBG展开在同一平面上,如图②,连结AB.
在直角三角形ABD中,根据勾股定理,得AB2=AD2+DB2=(12+5)2+92=370.
将四边形ACDF与四边形DCEB展开在同一平面上,如图③,连结AB.
在直角三角形AEB中,根据勾股定理,得AB2=AE2+EB2=(12+9)2+52=466.
因为340<370<466,
所以在长方体表面上由A点到B点的最短距离是如图①的情况,
此时AB≈18.44.
所以在长方体表面上由A点到B点的最短距离约为18.44.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
