浙教版八上1.4 全等三角形习题课件(26张)
文档属性
| 名称 | 浙教版八上1.4 全等三角形习题课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 420.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
第4节 全等三角形
第1章 三角形的初步认识
浙教版 八年级上
答案显示
习题链接
B
B
C
B
A
D
120°
7
C
答案显示
习题链接
其余的对应边是AB与BA;对应角是∠CBA与∠DAB,∠CAB与∠DBA,∠C与∠D
∠DAE=55°,
∠C=100°
180°
C
证明见习题
(1)翻折180°
(2)∠BAD=∠CAE
(3)相等,理由见习题
能,图略
(1)3
(2)①∠DBC=25°
②∠AFD=130°
1.下列图形是全等图形的是( )
B
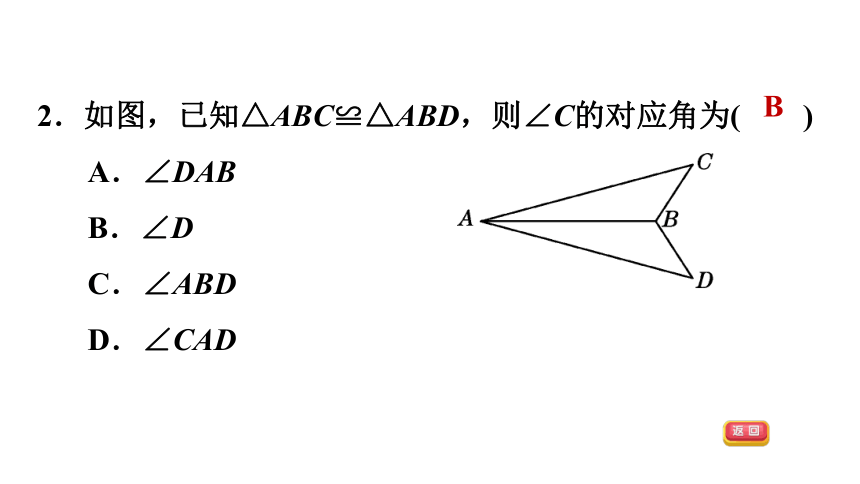
2.如图,已知△ABC≌△ABD,则∠C的对应角为( )
A.∠DAB
B.∠D
C.∠ABD
D.∠CAD
B
3.下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形都是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
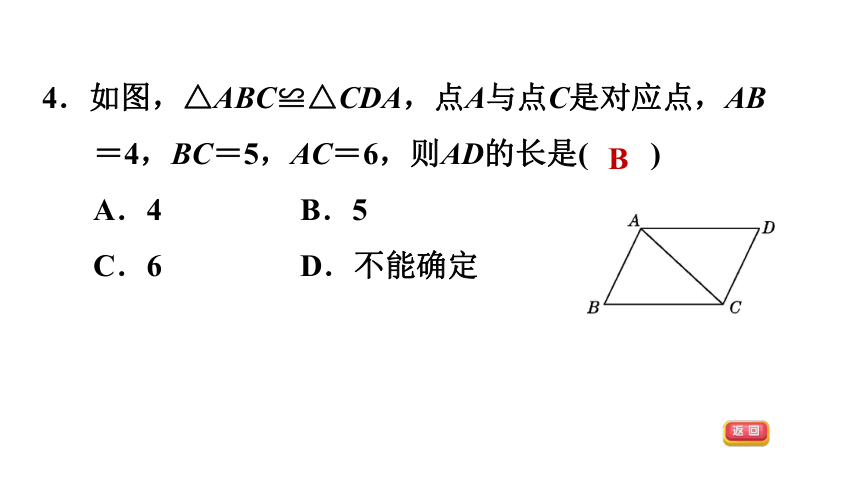
4.如图,△ABC≌△CDA,点A与点C是对应点,AB=4,BC=5,AC=6,则AD的长是( )
A.4 B.5
C.6 D.不能确定
B
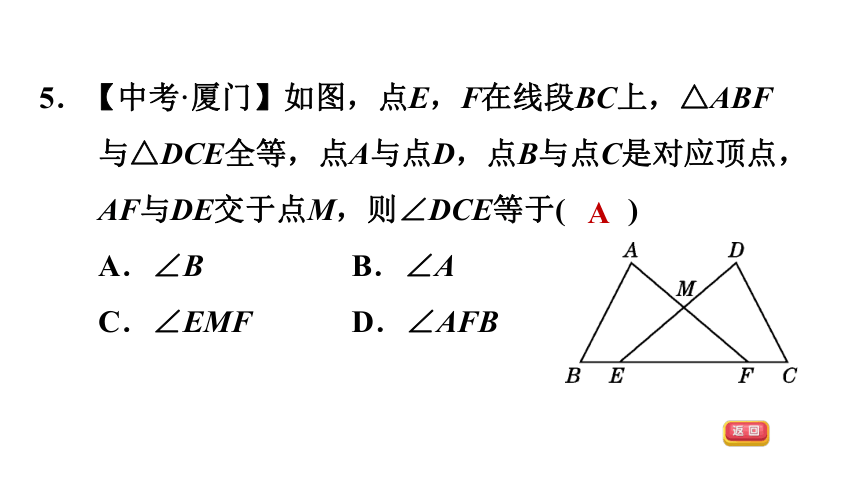
5.【中考·厦门】如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE等于( )
A.∠B B.∠A
C.∠EMF D.∠AFB
A
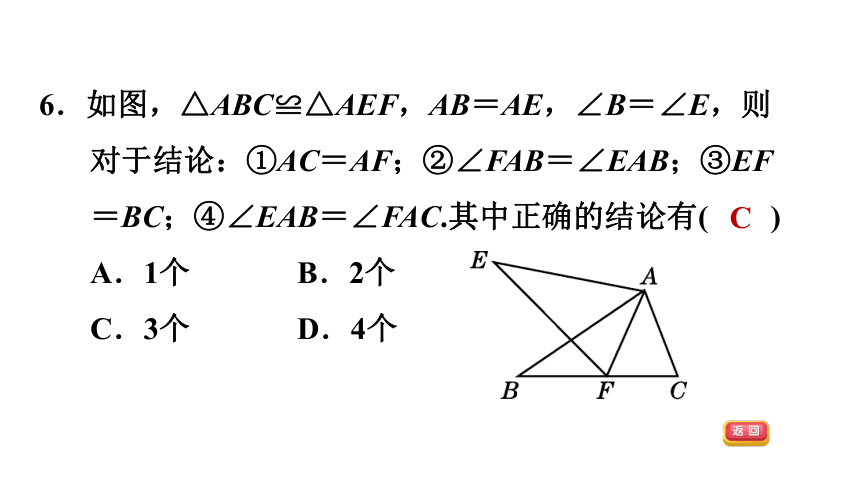
6.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的结论有( )
A.1个 B.2个
C.3个 D.4个
C
7.如图,D,E分别是△ABC的边AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
A.15° B.20°
C.25° D.30°
D
8.【中考·成都】如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,∠B=________.
120°
9.【2017·浙江衢州柯城期末】如图,已知△ABC≌ △DEF,点B,E,C,F在同一条直线上.若BC=5,BE=2,则BF=________.
7
10.如图,△ACB与△BDA全等,AC与BD对应,BC与AD对应,写出其余的对应边和对应角.
【点拨】利用图形特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边,两对应边的夹角是对应角,两对应角的夹边是对应边.当全等三角形的两组对应边(角)已确定时,剩下的一组边(角)就是对应边(角).
解:其余的对应边是AB与BA;对应角是∠CBA与∠DAB,∠CAB与∠DBA,∠C与∠D.
11.如图,已知△ADE≌△ACB,∠EAC=10°,∠B=25°,∠BAD=120°,求∠DAE,∠C的度数.
解:∵∠EAC=10°,∠BAD=120°,
∴∠DAE+∠CAB=∠BAD-∠EAC=120°-10°=110°.
∵△ADE≌△ACB,
∴∠DAE=∠CAB,∴∠DAE=∠CAB=55°,
∴∠C=180°-∠B-∠CAB=180°-25°-55°=100°.
12.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF.若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
A.3 B.4
C.6 D.8
C
13.如图是由4个相同的小正方形组成的网格图,已知△ABC≌△DBE,则∠1+∠2=________.
180°
14.如图,△ABC≌△ABD,点E在边AB上,CE∥BD.
求证:∠CEB=∠CBE.
证明:∵△ABC≌△ABD,
∴∠ABC=∠ABD.
∵CE∥BD,
∴∠CEB=∠DBE,
∴∠CEB=∠CBE.
15.如图,已知△ABE≌△ACD,且AB=AC,
(1)说明△ABE经过怎样的变化后可与△ACD重合.
解:△ABE翻折180°后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
解:∠BAD=∠CAE.理由如下:
∵△ABE≌△ACD,
∴∠B=∠C,∠AEB=∠ADC.
又∵∠B+∠BAD=∠ADC,
∠C+∠CAE=∠AEB,
∴∠BAD=∠CAE.
(3)BD与CE相等吗?为什么?
解:相等,
理由:∵△ABE≌△ACD,
∴BE=CD.
∴BE-DE=CD-DE,
即BD=CE.
16.如图是用10根火柴棒摆成的一个三角形,你能否移动其中的3根,摆出一对全等的三角形?画出你的移动方案.移动其中4根能否摆出一对全等的三角形?请画图说明.
解:能.移动3根,如图①所示;
移动4根,如图②所示.
17.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为________.
3
(2)若∠D=35°,∠C=60°.
①求∠DBC的度数;
解:∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°.
∵∠A+∠ABC+∠C=180°,
∴∠ABC=180°-∠A-∠C=85°,
∴∠DBC=∠ABC-∠DBE=85°-60°=25°.
(2)若∠D=35°,∠C=60°.
②求∠AFD的度数.
解:∵∠AEF是△DBE的一个外角,
∴∠AEF=∠D+∠DBE=35°+60°=95°.
∵∠AFD是△AEF的一个外角,
∴∠AFD=∠A+∠AEF=35°+95°=130°.
第4节 全等三角形
第1章 三角形的初步认识
浙教版 八年级上
答案显示
习题链接
B
B
C
B
A
D
120°
7
C
答案显示
习题链接
其余的对应边是AB与BA;对应角是∠CBA与∠DAB,∠CAB与∠DBA,∠C与∠D
∠DAE=55°,
∠C=100°
180°
C
证明见习题
(1)翻折180°
(2)∠BAD=∠CAE
(3)相等,理由见习题
能,图略
(1)3
(2)①∠DBC=25°
②∠AFD=130°
1.下列图形是全等图形的是( )
B
2.如图,已知△ABC≌△ABD,则∠C的对应角为( )
A.∠DAB
B.∠D
C.∠ABD
D.∠CAD
B
3.下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形都是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
4.如图,△ABC≌△CDA,点A与点C是对应点,AB=4,BC=5,AC=6,则AD的长是( )
A.4 B.5
C.6 D.不能确定
B
5.【中考·厦门】如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE等于( )
A.∠B B.∠A
C.∠EMF D.∠AFB
A
6.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的结论有( )
A.1个 B.2个
C.3个 D.4个
C
7.如图,D,E分别是△ABC的边AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
A.15° B.20°
C.25° D.30°
D
8.【中考·成都】如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,∠B=________.
120°
9.【2017·浙江衢州柯城期末】如图,已知△ABC≌ △DEF,点B,E,C,F在同一条直线上.若BC=5,BE=2,则BF=________.
7
10.如图,△ACB与△BDA全等,AC与BD对应,BC与AD对应,写出其余的对应边和对应角.
【点拨】利用图形特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边,两对应边的夹角是对应角,两对应角的夹边是对应边.当全等三角形的两组对应边(角)已确定时,剩下的一组边(角)就是对应边(角).
解:其余的对应边是AB与BA;对应角是∠CBA与∠DAB,∠CAB与∠DBA,∠C与∠D.
11.如图,已知△ADE≌△ACB,∠EAC=10°,∠B=25°,∠BAD=120°,求∠DAE,∠C的度数.
解:∵∠EAC=10°,∠BAD=120°,
∴∠DAE+∠CAB=∠BAD-∠EAC=120°-10°=110°.
∵△ADE≌△ACB,
∴∠DAE=∠CAB,∴∠DAE=∠CAB=55°,
∴∠C=180°-∠B-∠CAB=180°-25°-55°=100°.
12.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF.若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
A.3 B.4
C.6 D.8
C
13.如图是由4个相同的小正方形组成的网格图,已知△ABC≌△DBE,则∠1+∠2=________.
180°
14.如图,△ABC≌△ABD,点E在边AB上,CE∥BD.
求证:∠CEB=∠CBE.
证明:∵△ABC≌△ABD,
∴∠ABC=∠ABD.
∵CE∥BD,
∴∠CEB=∠DBE,
∴∠CEB=∠CBE.
15.如图,已知△ABE≌△ACD,且AB=AC,
(1)说明△ABE经过怎样的变化后可与△ACD重合.
解:△ABE翻折180°后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
解:∠BAD=∠CAE.理由如下:
∵△ABE≌△ACD,
∴∠B=∠C,∠AEB=∠ADC.
又∵∠B+∠BAD=∠ADC,
∠C+∠CAE=∠AEB,
∴∠BAD=∠CAE.
(3)BD与CE相等吗?为什么?
解:相等,
理由:∵△ABE≌△ACD,
∴BE=CD.
∴BE-DE=CD-DE,
即BD=CE.
16.如图是用10根火柴棒摆成的一个三角形,你能否移动其中的3根,摆出一对全等的三角形?画出你的移动方案.移动其中4根能否摆出一对全等的三角形?请画图说明.
解:能.移动3根,如图①所示;
移动4根,如图②所示.
17.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为________.
3
(2)若∠D=35°,∠C=60°.
①求∠DBC的度数;
解:∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°.
∵∠A+∠ABC+∠C=180°,
∴∠ABC=180°-∠A-∠C=85°,
∴∠DBC=∠ABC-∠DBE=85°-60°=25°.
(2)若∠D=35°,∠C=60°.
②求∠AFD的度数.
解:∵∠AEF是△DBE的一个外角,
∴∠AEF=∠D+∠DBE=35°+60°=95°.
∵∠AFD是△AEF的一个外角,
∴∠AFD=∠A+∠AEF=35°+95°=130°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
