浙教版八上1.6 尺规作图习题课件(21张)
文档属性
| 名称 | 浙教版八上1.6 尺规作图习题课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 452.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 08:24:19 | ||
图片预览




文档简介
(共21张PPT)
第6节 尺规作图
第1章 三角形的初步认识
浙教版 八年级上
答案显示
习题链接
D
D
A
C
C
D
10
(1)如图,点P为所求作.
(2)如图,OC为所求作.
(3)如图,MD为所求作.图略
B
答案显示
习题链接
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连结AC,则△ABC即为所求作的三角形(如图),图略
点P1,或点P2即为所求作的点,图略
(1)共九种,列举见习题
(2)只有a=2,b=3,c=4的三角形满足条件,图略
C1,C2即为所求位置,图略
满足条件的修建点有四处,即O1,O2,O3,O4,图略
1.尺规作图的画图工具是( )
A.刻度尺、圆规
B.三角板和量角器
C.直尺和量角器
D.没有刻度的直尺和圆规
D
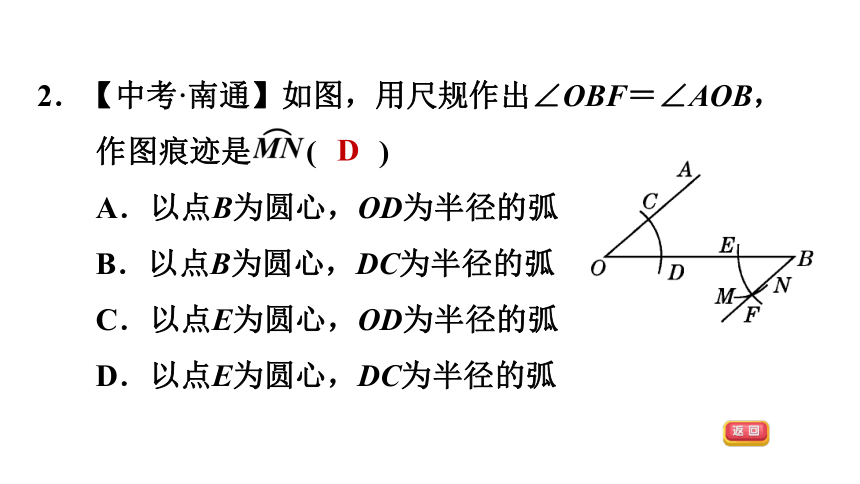
2.【中考·南通】如图,用尺规作出∠OBF=∠AOB,作图痕迹是 ( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
3.根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=1
D.∠C=90°,AB=6
A
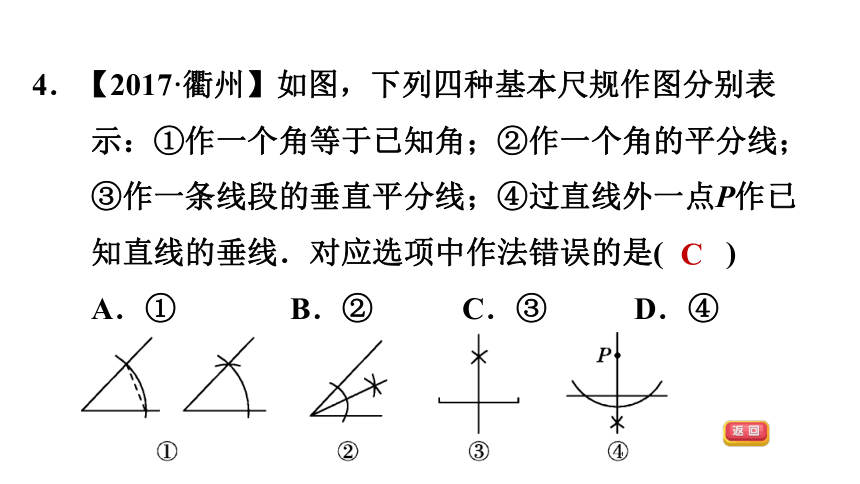
4.【2017·衢州】如图,下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线.对应选项中作法错误的是( )
A.① B.② C.③ D.④
C
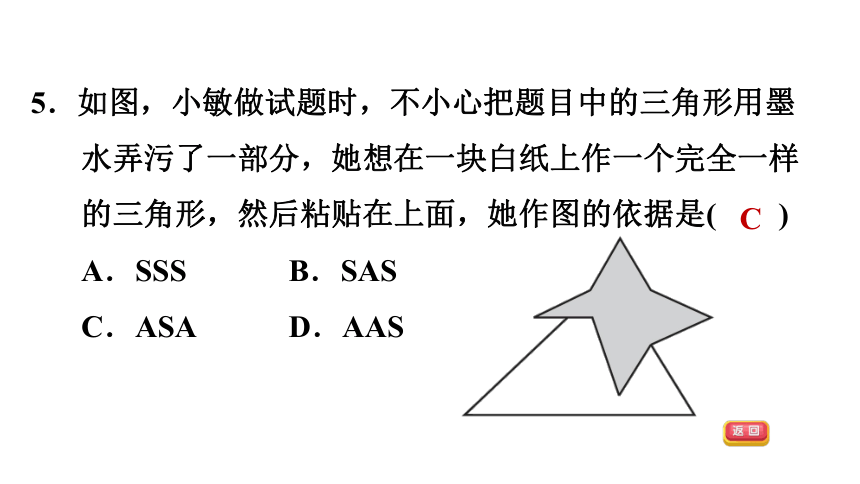
5.如图,小敏做试题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是( )
A.SSS B.SAS
C.ASA D.AAS
C
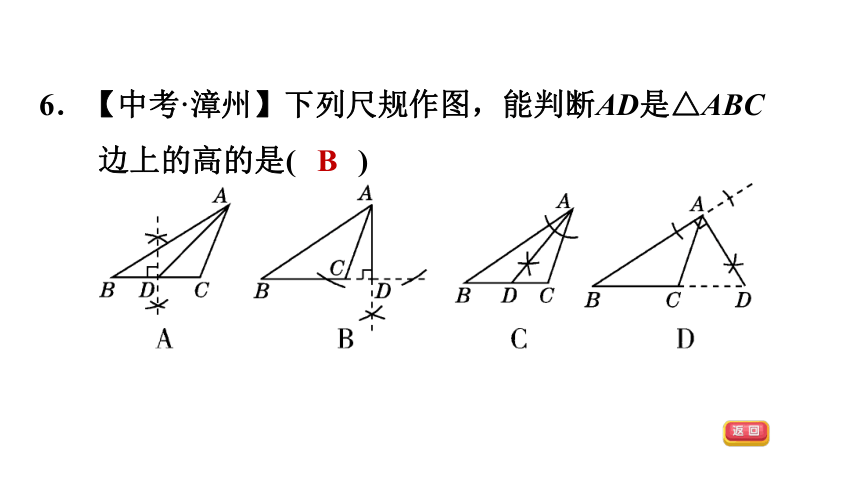
6.【中考·漳州】下列尺规作图,能判断AD是△ABC边上的高的是( )
B
7.【2018·安顺】已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
D
8.【中考·长春】如图,在△ABC中,AB>AC.按以下步骤作图:分别以B和C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;作直线MN交AB于点D;连结CD.若AB=6,AC=4,则△ACD的周长为________.
10
【点拨】根据题中作法可知:MN是BC的垂直平分线,∴BD=CD.
∴△ADC的周长为AD+CD+AC=AD+BD+AC=AB+AC=6+4=10.
9.【2017·贵港】尺规作图.(不写作法,保留作图痕迹)已知线段a和∠AOB,点M在OB上,如图所示.
(1)在OA边上作点P,使OP=2a;
(2)作∠AOB的平分线;
(3)过点M作OB的垂线.
解: (1)如图,点P为所求作.
(2)如图,OC为所求作.
(3)如图,MD为所求作.
10.【中考·青岛】如图,已知线段a,c,∠α.
求作△ABC,使BC=a,AB=c,∠ABC=∠α.
解: (1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连结AC,则△ABC即为所求作的三角形(如图).
11.【2017·青岛】已知:如图,四边形ABCD.
求作:点P,使∠PCB=∠B,且点P到边AD和CD的距离相等.
解:如图,点P1,或点P2即为所求作的点.
12.【中考·德州】有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不
要求写出画法)
【点拨】由题意可知,点C应满足两个条件:①在线段AB的垂直平分线上;②在两条公路夹角的平分线上.故点C为这两条线的交点.先作线段AB的垂直平分线FG,再作两条公路夹角的平分线OD或OE,找出直线FG与射线OD,OE的交点,即可得到点C的位置.
解:如图,C1,C2即为所求位置.
13.【中考·杭州】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形,请列举出所有满足条件的三角形;
解:共九种:(2,2,2),(2,2,3),(2,3,3),(2,3,4),(2,4,4),(3,3,3),(3,3,4),(3,4,4),(4,4,4).
(2)用直尺和圆规作出三边满足a<b<c的三角形.(用给定的单位长度,不写作法,保留作图痕迹)
解:只有a=2,b=3,c=4的三角形满足条件.如图,△ABC即为满足条件的三角形.
14.“角平分线上的点到角的两边的距离相等,到角的两边的距离相等的点在角的平分线上”,如图①所示.
(1)若∠BAD=∠CAD,且DB⊥AB于点B,DC⊥AC于点C,则BD=CD;
(2)若DB⊥AB于点B,DC⊥AC于点C,
且BD=CD,则∠BAD=∠CAD.
试利用上述知识,解决下面的问题:三条公路两两相交于E,F,G三点,如图②所示,现计划修建一个商品超市,要求这个超市到三条公路的距离相等.问:可供选择的地方有多少处?
解:如图,满足条件的修建点有四处,即O1,O2,O3,O4.
第6节 尺规作图
第1章 三角形的初步认识
浙教版 八年级上
答案显示
习题链接
D
D
A
C
C
D
10
(1)如图,点P为所求作.
(2)如图,OC为所求作.
(3)如图,MD为所求作.图略
B
答案显示
习题链接
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连结AC,则△ABC即为所求作的三角形(如图),图略
点P1,或点P2即为所求作的点,图略
(1)共九种,列举见习题
(2)只有a=2,b=3,c=4的三角形满足条件,图略
C1,C2即为所求位置,图略
满足条件的修建点有四处,即O1,O2,O3,O4,图略
1.尺规作图的画图工具是( )
A.刻度尺、圆规
B.三角板和量角器
C.直尺和量角器
D.没有刻度的直尺和圆规
D
2.【中考·南通】如图,用尺规作出∠OBF=∠AOB,作图痕迹是 ( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
3.根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=1
D.∠C=90°,AB=6
A
4.【2017·衢州】如图,下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线.对应选项中作法错误的是( )
A.① B.② C.③ D.④
C
5.如图,小敏做试题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是( )
A.SSS B.SAS
C.ASA D.AAS
C
6.【中考·漳州】下列尺规作图,能判断AD是△ABC边上的高的是( )
B
7.【2018·安顺】已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
D
8.【中考·长春】如图,在△ABC中,AB>AC.按以下步骤作图:分别以B和C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;作直线MN交AB于点D;连结CD.若AB=6,AC=4,则△ACD的周长为________.
10
【点拨】根据题中作法可知:MN是BC的垂直平分线,∴BD=CD.
∴△ADC的周长为AD+CD+AC=AD+BD+AC=AB+AC=6+4=10.
9.【2017·贵港】尺规作图.(不写作法,保留作图痕迹)已知线段a和∠AOB,点M在OB上,如图所示.
(1)在OA边上作点P,使OP=2a;
(2)作∠AOB的平分线;
(3)过点M作OB的垂线.
解: (1)如图,点P为所求作.
(2)如图,OC为所求作.
(3)如图,MD为所求作.
10.【中考·青岛】如图,已知线段a,c,∠α.
求作△ABC,使BC=a,AB=c,∠ABC=∠α.
解: (1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连结AC,则△ABC即为所求作的三角形(如图).
11.【2017·青岛】已知:如图,四边形ABCD.
求作:点P,使∠PCB=∠B,且点P到边AD和CD的距离相等.
解:如图,点P1,或点P2即为所求作的点.
12.【中考·德州】有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不
要求写出画法)
【点拨】由题意可知,点C应满足两个条件:①在线段AB的垂直平分线上;②在两条公路夹角的平分线上.故点C为这两条线的交点.先作线段AB的垂直平分线FG,再作两条公路夹角的平分线OD或OE,找出直线FG与射线OD,OE的交点,即可得到点C的位置.
解:如图,C1,C2即为所求位置.
13.【中考·杭州】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形,请列举出所有满足条件的三角形;
解:共九种:(2,2,2),(2,2,3),(2,3,3),(2,3,4),(2,4,4),(3,3,3),(3,3,4),(3,4,4),(4,4,4).
(2)用直尺和圆规作出三边满足a<b<c的三角形.(用给定的单位长度,不写作法,保留作图痕迹)
解:只有a=2,b=3,c=4的三角形满足条件.如图,△ABC即为满足条件的三角形.
14.“角平分线上的点到角的两边的距离相等,到角的两边的距离相等的点在角的平分线上”,如图①所示.
(1)若∠BAD=∠CAD,且DB⊥AB于点B,DC⊥AC于点C,则BD=CD;
(2)若DB⊥AB于点B,DC⊥AC于点C,
且BD=CD,则∠BAD=∠CAD.
试利用上述知识,解决下面的问题:三条公路两两相交于E,F,G三点,如图②所示,现计划修建一个商品超市,要求这个超市到三条公路的距离相等.问:可供选择的地方有多少处?
解:如图,满足条件的修建点有四处,即O1,O2,O3,O4.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
