浙教版八上第1章三角形的初步知识全章热门考点整合课件(30张)
文档属性
| 名称 | 浙教版八上第1章三角形的初步知识全章热门考点整合课件(30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 558.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 00:00:00 | ||
图片预览






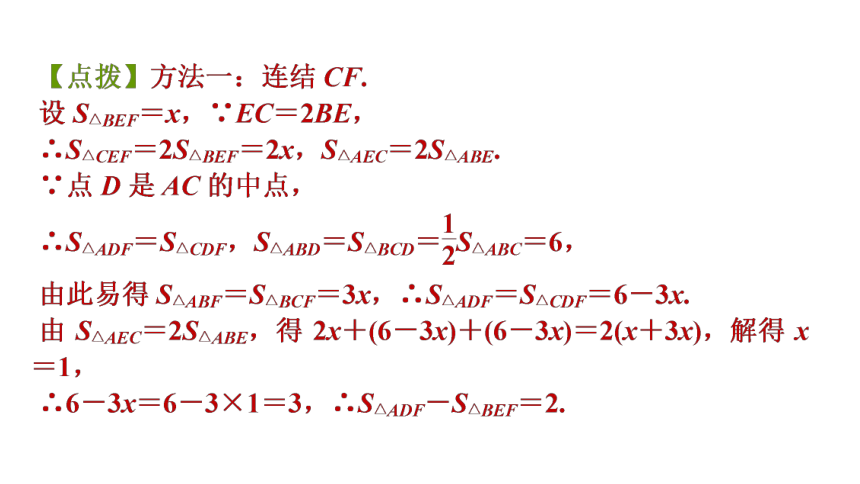
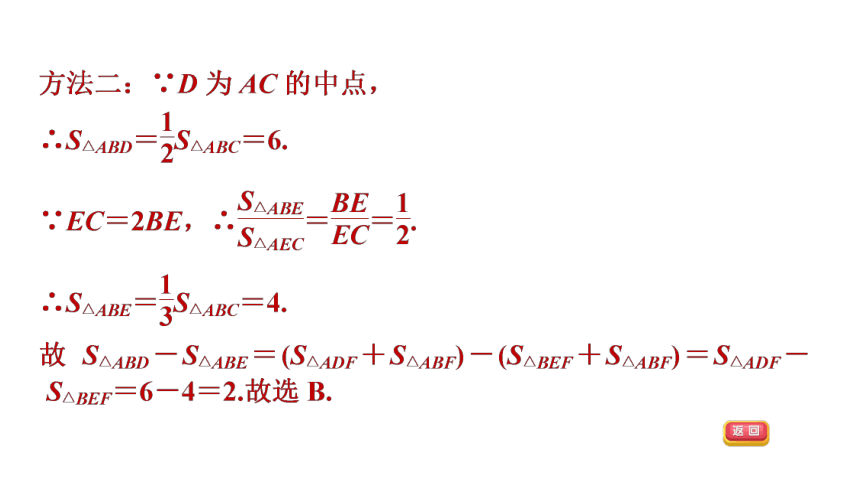
文档简介
(共30张PPT)
全章热门考点整合
第1章 三角形的初步认识
浙教版 八年级上
答案显示
习题链接
(1)3;△ACE,
△ACD,△ACB
(2)BCE;CDE
(3)CE
A
C
AB与AC,AE与AD,BE与CD是对应边;∠B与∠C,∠2与∠1,∠BAE与∠CAD是对应角.
EB的长为1
(1)6;12
(2)45;45
(3)90;90
C
∠B=50°
B
答案显示
习题链接
∠DFB=60°
∠ADC=75°
4
(1)证明见习题;
(2)a=5 cm
△ABC是钝角三角形
1.如图,在△ABC中, D是BC边上的一点,E是AD上一点.
(1)以AC为边的三角形共有________个,它们是____________________________;
(2)∠1是△________和△________的内角;
(3)在△ACE中,∠CAE的对边是________.
3
△ACE,△ACD,△ACB
BCE
CDE
CE
2.有下列命题:①真命题都是定理;②定理都是真命题;③假命题不是命题;④基本事实都是命题.其中是真命题的有( )
A.2个 B.3个 C.4个 D.1个
A
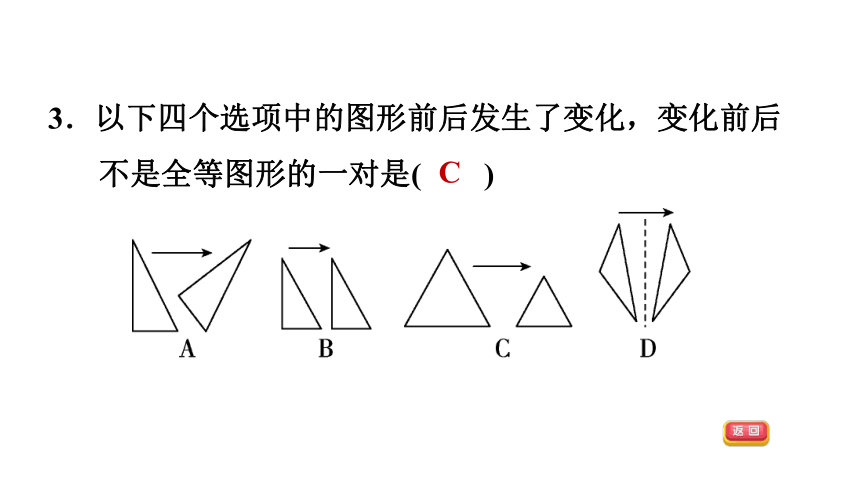
3.以下四个选项中的图形前后发生了变化,变化前后不是全等图形的一对是( )
C
4.如图,已知△ABE与△ADC全等,∠1=∠2,∠B=∠C,指出全等三角形中的对应边和对应角.
解:AB与AC,AE与AD,BE与CD是对应边;∠B与∠C,∠2与∠1,∠BAE与∠CAD是对应角.
5.如图,D为△ABC中AC边上一点,AD=1,DC=2,AB=4,E是AB上一点,且△DEC的面积等于△ABC面积的一半,求EB的长.
解:如图,过点E作EF⊥AC于点F,
【点拨】同(等)高的两个三角形的面积比等于底边长的比.
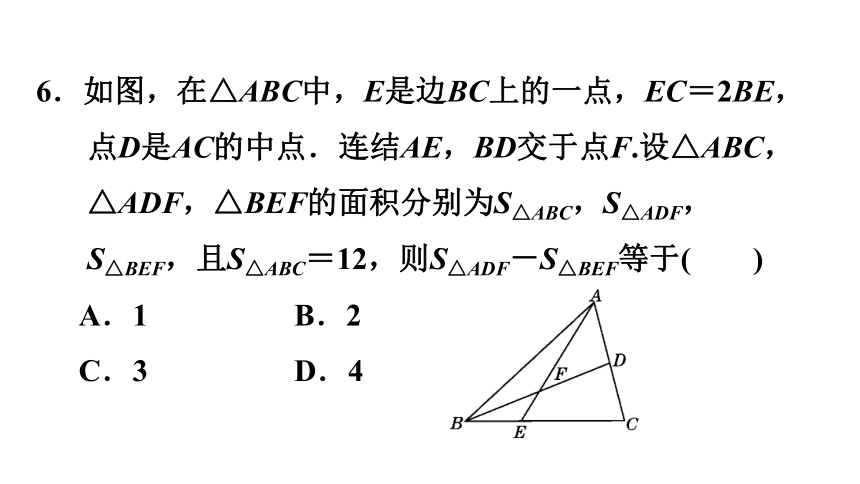
6.如图,在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点.连结AE,BD交于点F.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF等于( )
A.1 B.2
C.3 D.4
7.如图,在△ABC中,AF是中线,AE是角平分线,AD是高,∠BAC=90°,FC=6,则根据图形填空:
(1)BF=________,BC=________;
(2)∠BAE=________°,∠CAE=________°;
(3)∠ADB=________°,∠ADC=________°.
6
12
45
45
90
90
8.下列各组数可能是一个三角形的边长的是( )
A.5,1,7 B.5,12,17
C.5,7,7 D.11,12,23
C
9.如图,在△ABC中,∠A=46°,CE平分∠ACB,点B,C,D在同一条直线上,FD∥EC,∠D=42°,求∠B的度数.
【点拨】本题运用了综合法和转化思想,借助平行线把与△ABC无关的已知角转化成△ABC中的∠BCE,再结合角平分线的定义进一步运用三角形内角和定理解决问题.
解:∵FD∥EC,∠D=42°,
∴∠BCE=∠D=42°.
∵CE平分∠ACB,
∴∠ACB=2∠BCE=84°.
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
10.如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
解:∵∠B+∠C+∠BAC=180°,
∠B=30°,∠C=50°,
∴∠BAC=180°-30°-50°=100°.
(2)∠DAE与∠C-∠B有何关系?
11.如图,已知△ABC≌△ADE,BC的延长线交DE于点F,交AD于点M.若∠D=25°,∠AED=105°,∠DAC=10°,求∠DFB的度数.
解:∵∠D=25°,∠AED=105°,∴∠DAE=50°.
又∵△ABC≌△ADE,
∴∠B=∠D=25°,∠BAC=∠DAE=50°.
∵∠DAC=10°,∴∠BAD=60°,
∴∠AMF=∠BAD+∠B=60°+25°=85°,
∴∠DFB=∠AMF-∠D=85°-25°=60°.
12.如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点OE⊥AC于E,OE=2,求AB与CD之间的距离.
解:如图,过点O作OF⊥AB,垂足为F,FO的延长线与CD交于点G. ∵AB∥CD,OF⊥AB,
∴OG⊥CD,即FG⊥CD,FG⊥AB.
又∵AO,CO分别平分∠BAC,∠ACD,
且OF⊥AB,OE⊥AC,OG⊥CD,
∴OF=OE=OG=2,∴FG=OF+OG=2+2=4,
即AB与CD之间的距离为4.
13.如图,在直角三角形ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连结AD,AD将∠CAB分成两个角,且∠1:∠2=2:5,求∠ADC的度数.
解:∵∠1:∠2=2:5,∴设∠1=2x,则∠2=5x.
∵DE是线段AB的垂直平分线,∴AD=BD.
∴△ADB是等腰三角形.∴∠B=∠2=5x.
∴∠ADC=∠2+∠B=10x.
在△ADC中,2x+10x+90°=180°,
解得x=7.5°,∴∠ADC=10x=75°.
14.课间,小明拿着老师的等腰直角三角板玩,不小心掉到了两堆砖块之间,如图所示.
(1)求证:△ADC≌△CEB;
(2)已知DE=35 cm,请你帮小明求出砖块的厚度a的大小.(每块砖块的厚度相等)
解:由题意得AD=4a,BE=3a.
由(1)得△ADC≌△CEB,∴DC=BE=3a,CE=AD=4a,∴DE=DC+CE=7a.∵DE=35 cm,∴a=5 cm.
15.在△ABC中,若∠A=2∠B=3∠C,试判断这个三角形的形状.
【点拨】求有一定关系的三角形的三个内角的度数时,常把三角形的内角和为180°作为相等关系,从而运用方程思想来解决问题.
全章热门考点整合
第1章 三角形的初步认识
浙教版 八年级上
答案显示
习题链接
(1)3;△ACE,
△ACD,△ACB
(2)BCE;CDE
(3)CE
A
C
AB与AC,AE与AD,BE与CD是对应边;∠B与∠C,∠2与∠1,∠BAE与∠CAD是对应角.
EB的长为1
(1)6;12
(2)45;45
(3)90;90
C
∠B=50°
B
答案显示
习题链接
∠DFB=60°
∠ADC=75°
4
(1)证明见习题;
(2)a=5 cm
△ABC是钝角三角形
1.如图,在△ABC中, D是BC边上的一点,E是AD上一点.
(1)以AC为边的三角形共有________个,它们是____________________________;
(2)∠1是△________和△________的内角;
(3)在△ACE中,∠CAE的对边是________.
3
△ACE,△ACD,△ACB
BCE
CDE
CE
2.有下列命题:①真命题都是定理;②定理都是真命题;③假命题不是命题;④基本事实都是命题.其中是真命题的有( )
A.2个 B.3个 C.4个 D.1个
A
3.以下四个选项中的图形前后发生了变化,变化前后不是全等图形的一对是( )
C
4.如图,已知△ABE与△ADC全等,∠1=∠2,∠B=∠C,指出全等三角形中的对应边和对应角.
解:AB与AC,AE与AD,BE与CD是对应边;∠B与∠C,∠2与∠1,∠BAE与∠CAD是对应角.
5.如图,D为△ABC中AC边上一点,AD=1,DC=2,AB=4,E是AB上一点,且△DEC的面积等于△ABC面积的一半,求EB的长.
解:如图,过点E作EF⊥AC于点F,
【点拨】同(等)高的两个三角形的面积比等于底边长的比.
6.如图,在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点.连结AE,BD交于点F.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF等于( )
A.1 B.2
C.3 D.4
7.如图,在△ABC中,AF是中线,AE是角平分线,AD是高,∠BAC=90°,FC=6,则根据图形填空:
(1)BF=________,BC=________;
(2)∠BAE=________°,∠CAE=________°;
(3)∠ADB=________°,∠ADC=________°.
6
12
45
45
90
90
8.下列各组数可能是一个三角形的边长的是( )
A.5,1,7 B.5,12,17
C.5,7,7 D.11,12,23
C
9.如图,在△ABC中,∠A=46°,CE平分∠ACB,点B,C,D在同一条直线上,FD∥EC,∠D=42°,求∠B的度数.
【点拨】本题运用了综合法和转化思想,借助平行线把与△ABC无关的已知角转化成△ABC中的∠BCE,再结合角平分线的定义进一步运用三角形内角和定理解决问题.
解:∵FD∥EC,∠D=42°,
∴∠BCE=∠D=42°.
∵CE平分∠ACB,
∴∠ACB=2∠BCE=84°.
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
10.如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
解:∵∠B+∠C+∠BAC=180°,
∠B=30°,∠C=50°,
∴∠BAC=180°-30°-50°=100°.
(2)∠DAE与∠C-∠B有何关系?
11.如图,已知△ABC≌△ADE,BC的延长线交DE于点F,交AD于点M.若∠D=25°,∠AED=105°,∠DAC=10°,求∠DFB的度数.
解:∵∠D=25°,∠AED=105°,∴∠DAE=50°.
又∵△ABC≌△ADE,
∴∠B=∠D=25°,∠BAC=∠DAE=50°.
∵∠DAC=10°,∴∠BAD=60°,
∴∠AMF=∠BAD+∠B=60°+25°=85°,
∴∠DFB=∠AMF-∠D=85°-25°=60°.
12.如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点OE⊥AC于E,OE=2,求AB与CD之间的距离.
解:如图,过点O作OF⊥AB,垂足为F,FO的延长线与CD交于点G. ∵AB∥CD,OF⊥AB,
∴OG⊥CD,即FG⊥CD,FG⊥AB.
又∵AO,CO分别平分∠BAC,∠ACD,
且OF⊥AB,OE⊥AC,OG⊥CD,
∴OF=OE=OG=2,∴FG=OF+OG=2+2=4,
即AB与CD之间的距离为4.
13.如图,在直角三角形ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连结AD,AD将∠CAB分成两个角,且∠1:∠2=2:5,求∠ADC的度数.
解:∵∠1:∠2=2:5,∴设∠1=2x,则∠2=5x.
∵DE是线段AB的垂直平分线,∴AD=BD.
∴△ADB是等腰三角形.∴∠B=∠2=5x.
∴∠ADC=∠2+∠B=10x.
在△ADC中,2x+10x+90°=180°,
解得x=7.5°,∴∠ADC=10x=75°.
14.课间,小明拿着老师的等腰直角三角板玩,不小心掉到了两堆砖块之间,如图所示.
(1)求证:△ADC≌△CEB;
(2)已知DE=35 cm,请你帮小明求出砖块的厚度a的大小.(每块砖块的厚度相等)
解:由题意得AD=4a,BE=3a.
由(1)得△ADC≌△CEB,∴DC=BE=3a,CE=AD=4a,∴DE=DC+CE=7a.∵DE=35 cm,∴a=5 cm.
15.在△ABC中,若∠A=2∠B=3∠C,试判断这个三角形的形状.
【点拨】求有一定关系的三角形的三个内角的度数时,常把三角形的内角和为180°作为相等关系,从而运用方程思想来解决问题.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
