浙教版八年级下册数学第四章4.1多边形(1)课件(共21张PPT)
文档属性
| 名称 | 浙教版八年级下册数学第四章4.1多边形(1)课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 20:48:45 | ||
图片预览





文档简介
(共21张PPT)
你会画四边形吗?如果会请你画一个!
你会画五边形吗?那六边形呢? ………….
你能根据三角形的定义类比出四边形的定义和特点吗?
那多边形的定义呢?
定义:
由不在同一条直线上的三条线段首尾顺次相接所形成的图形叫三角形 。
A
B
C
四边形:由不在同一条直线上的四条线段首尾顺次相接所形成的图形叫四边形 。
多边形:在同一平面内,由任意
两条都不在同一条直线上的若干
条线段(线段的条数不小于3)
首尾顺次相接形成的图形叫多边形 。
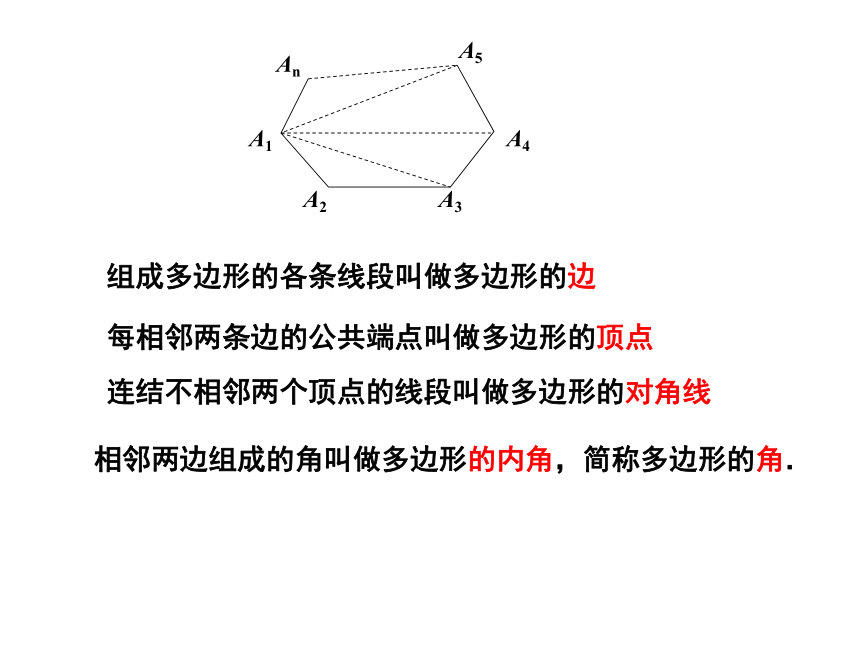
每相邻两条边的公共端点叫做多边形的顶点
连结不相邻两个顶点的线段叫做多边形的对角线
相邻两边组成的角叫做多边形的内角,简称多边形的角.
组成多边形的各条线段叫做多边形的边
顶点
内角
边
对角线
外角
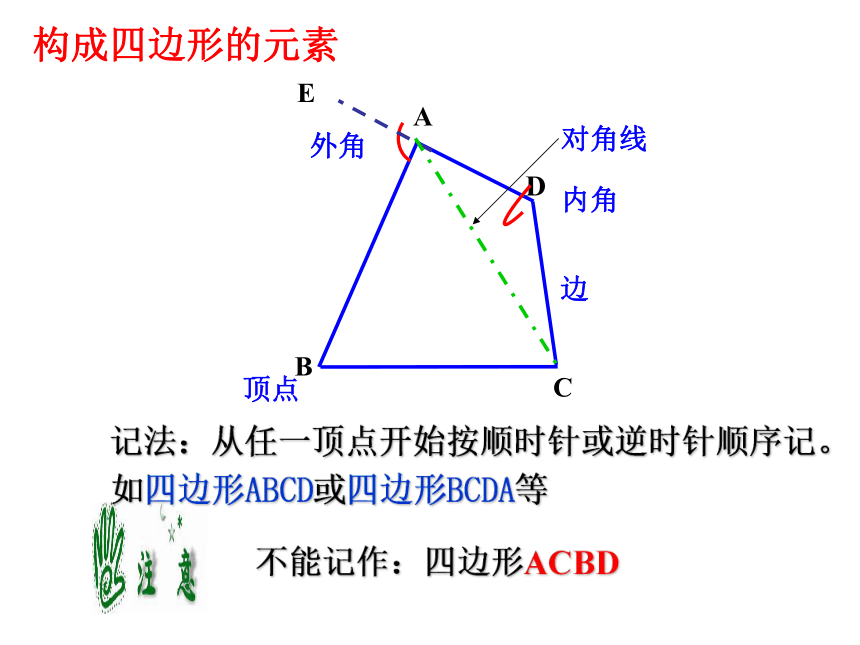
构成四边形的元素
不能记作:四边形ACBD
记法:从任一顶点开始按顺时针或逆时针顺序记。如四边形ABCD或四边形BCDA等
拿起你手中的四边形,找出四个内角,并作上记号,请剪下四个内角,把它们拼在一起(四个角的顶点重合),你发现了这四个内角有什么规律?和你猜得是否一样。
你能验证你的结论吗?前后同学交流一下你所用的方法。
四边形的内角和等于360°.
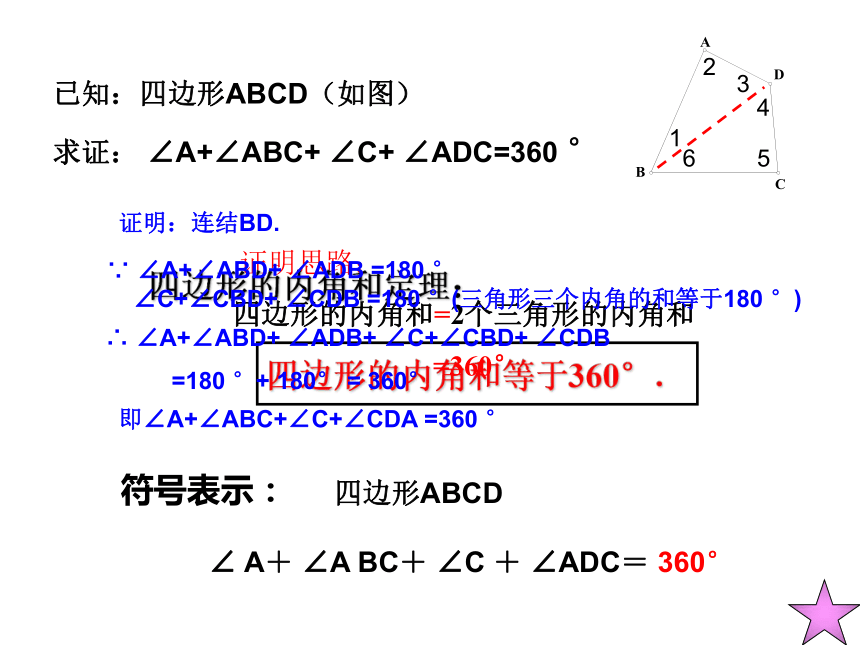
证明思路:
四边形的内角和=2个三角形的内角和
=360°
四边形的内角和定理:
符号表示:
四边形ABCD
∠ A+ ∠A BC+ ∠C + ∠ADC= 360°
已知:四边形ABCD(如图)
求证: ∠A+∠ABC+ ∠C+ ∠ADC=360 °
四边形内角和定理:
四边形的内角和等于360 °
请说出什么是三角形的外角?
三角形的外角和等于多少?
360°
外角
已知:如图,∠5 ,∠ 6,∠7 ,∠8
是四边形的四个外角。
求:∠ 5+∠ 6+ ∠7 +∠8 =?
你刚才所画的四边形,并画出它每个的不同顶点的一个外角,求出外角和等于多少度?
解: ∵∠ 1+∠5 =∠2+ ∠6= ∠3+∠7 =∠ 4+∠8= 180°
∴ ∠ 1+∠5 +∠2+ ∠6+ ∠3+∠7+ ∠ 4+∠8 =4× 180°= 720°
即: (∠ 1+∠2 +∠ 3 + ∠4)+ (∠5 +∠ 6 + ∠ 7 +∠8) = 720°
∵ ∠1 +∠ 2 + ∠ 3 +∠4=360°(根据四边形的内角和是360°)
∴ ∠5+∠ 6+ ∠ 7 +∠8 = 720°- 360°= 360°
推论: 四边形的外角和等于360°
1、已知四边形ABCD中, ∠A=∠B=∠C=90°
则∠D=_____.
90 °
2、已知四边形ABCD中, ∠A=80 °, ∠B=60°, ∠C=70°则∠D=_____.
150 °
小试牛刀:
3、已知四边形ABCD中,∠A与∠C互补.
如果∠B=80°,求∠D的度数.
∠D=100°
4、在四边形ABCD中,∠B=90°,
∠A、∠C、∠D的度数比为1∶3∶5,
则∠A=________度,∠C=________度,
∠D=________度.
30°
90°
150°
例1 如图,四边形风筝的四个内角∠A,∠B,∠C,∠D的度数之比为1:1:0.6:1,求它的四个内角的度数.
已知:如图,直线AD⊥ AB,垂足为A,直线CD⊥ BC,垂足为C
(1) ∠1与∠B之间有什么关系?
(2)图中有与 ∠B相等的角吗?
若有,请指出并说明理由。
A
B
C
D
1
2
3
通过本节课的学习,
知识上你有哪些收获?
你学到了哪些方法?
你还有什么困惑吗?
一个定义,一个定理,一个推论
2. 重要数学方法
三角形的概念 四边形的概念
四边形问题 三角形问题
类比
转化
(已知)
(未知)
类比
转化
(未知)
(已知)
1.书本P77-78的作业题A
2.作业本(1)4.1;
作业要认真完成
思考题:
探索五边形,六边形, ……, n边形的内
外角和,你能否发现并找出n边形内外角
和的计算规律?
你会画四边形吗?如果会请你画一个!
你会画五边形吗?那六边形呢? ………….
你能根据三角形的定义类比出四边形的定义和特点吗?
那多边形的定义呢?
定义:
由不在同一条直线上的三条线段首尾顺次相接所形成的图形叫三角形 。
A
B
C
四边形:由不在同一条直线上的四条线段首尾顺次相接所形成的图形叫四边形 。
多边形:在同一平面内,由任意
两条都不在同一条直线上的若干
条线段(线段的条数不小于3)
首尾顺次相接形成的图形叫多边形 。
每相邻两条边的公共端点叫做多边形的顶点
连结不相邻两个顶点的线段叫做多边形的对角线
相邻两边组成的角叫做多边形的内角,简称多边形的角.
组成多边形的各条线段叫做多边形的边
顶点
内角
边
对角线
外角
构成四边形的元素
不能记作:四边形ACBD
记法:从任一顶点开始按顺时针或逆时针顺序记。如四边形ABCD或四边形BCDA等
拿起你手中的四边形,找出四个内角,并作上记号,请剪下四个内角,把它们拼在一起(四个角的顶点重合),你发现了这四个内角有什么规律?和你猜得是否一样。
你能验证你的结论吗?前后同学交流一下你所用的方法。
四边形的内角和等于360°.
证明思路:
四边形的内角和=2个三角形的内角和
=360°
四边形的内角和定理:
符号表示:
四边形ABCD
∠ A+ ∠A BC+ ∠C + ∠ADC= 360°
已知:四边形ABCD(如图)
求证: ∠A+∠ABC+ ∠C+ ∠ADC=360 °
四边形内角和定理:
四边形的内角和等于360 °
请说出什么是三角形的外角?
三角形的外角和等于多少?
360°
外角
已知:如图,∠5 ,∠ 6,∠7 ,∠8
是四边形的四个外角。
求:∠ 5+∠ 6+ ∠7 +∠8 =?
你刚才所画的四边形,并画出它每个的不同顶点的一个外角,求出外角和等于多少度?
解: ∵∠ 1+∠5 =∠2+ ∠6= ∠3+∠7 =∠ 4+∠8= 180°
∴ ∠ 1+∠5 +∠2+ ∠6+ ∠3+∠7+ ∠ 4+∠8 =4× 180°= 720°
即: (∠ 1+∠2 +∠ 3 + ∠4)+ (∠5 +∠ 6 + ∠ 7 +∠8) = 720°
∵ ∠1 +∠ 2 + ∠ 3 +∠4=360°(根据四边形的内角和是360°)
∴ ∠5+∠ 6+ ∠ 7 +∠8 = 720°- 360°= 360°
推论: 四边形的外角和等于360°
1、已知四边形ABCD中, ∠A=∠B=∠C=90°
则∠D=_____.
90 °
2、已知四边形ABCD中, ∠A=80 °, ∠B=60°, ∠C=70°则∠D=_____.
150 °
小试牛刀:
3、已知四边形ABCD中,∠A与∠C互补.
如果∠B=80°,求∠D的度数.
∠D=100°
4、在四边形ABCD中,∠B=90°,
∠A、∠C、∠D的度数比为1∶3∶5,
则∠A=________度,∠C=________度,
∠D=________度.
30°
90°
150°
例1 如图,四边形风筝的四个内角∠A,∠B,∠C,∠D的度数之比为1:1:0.6:1,求它的四个内角的度数.
已知:如图,直线AD⊥ AB,垂足为A,直线CD⊥ BC,垂足为C
(1) ∠1与∠B之间有什么关系?
(2)图中有与 ∠B相等的角吗?
若有,请指出并说明理由。
A
B
C
D
1
2
3
通过本节课的学习,
知识上你有哪些收获?
你学到了哪些方法?
你还有什么困惑吗?
一个定义,一个定理,一个推论
2. 重要数学方法
三角形的概念 四边形的概念
四边形问题 三角形问题
类比
转化
(已知)
(未知)
类比
转化
(未知)
(已知)
1.书本P77-78的作业题A
2.作业本(1)4.1;
作业要认真完成
思考题:
探索五边形,六边形, ……, n边形的内
外角和,你能否发现并找出n边形内外角
和的计算规律?
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
