5.1 矩形（1） 同步训练（含解析）

初中数学浙教版八年级下册5.1 矩形（1） 同步训练
一、基础夯实
1.如图，在矩形AOBC中，A(-2，0)，B(0，1)．若正比例函数y=kx的图象经过点C，则k的值为（ ??）

A.?- ?????????????????????????????????????????B.??????????????????????????????????????????C.?-2?????????????????????????????????????????D.?2
2.如图，矩形ABCD的对角线交于点O．若∠BAO=55°，则∠AOD等于(??? )

A.?110°????????????????????????????????????B.?115°????????????????????????????????????C.?120°????????????????????????????????????D.?125°
3.矩形不一定具有的性质是（ ??）
A.?对角线互相平分????????????????B.?对角线互相垂直????????????????????C.?对角线相等????????????????D.?是轴对称图形
4.如图，在矩形ABCD中，对角线AC、BD交于点O，以下说法不一定成立的是（?? ）
A.?∠ABC=90°????????????????????????????B.?AC=BD????????????????????????????C.?OA=OB????????????????????????????D.?OA=AD
5.如图， 矩形 的对角线 ， 交于点 ， ， ，则 的长为 （??? ）
A.?4cm??????????????????????????????????B.?4cm??????????????????????????????????C.?2cm??????????????????????????????????D.?2cm
6.已知一个矩形的对角线的长为4，它们的夹角是60°，则这个矩形的较短的边长为________，面积为 ________. 21教育网
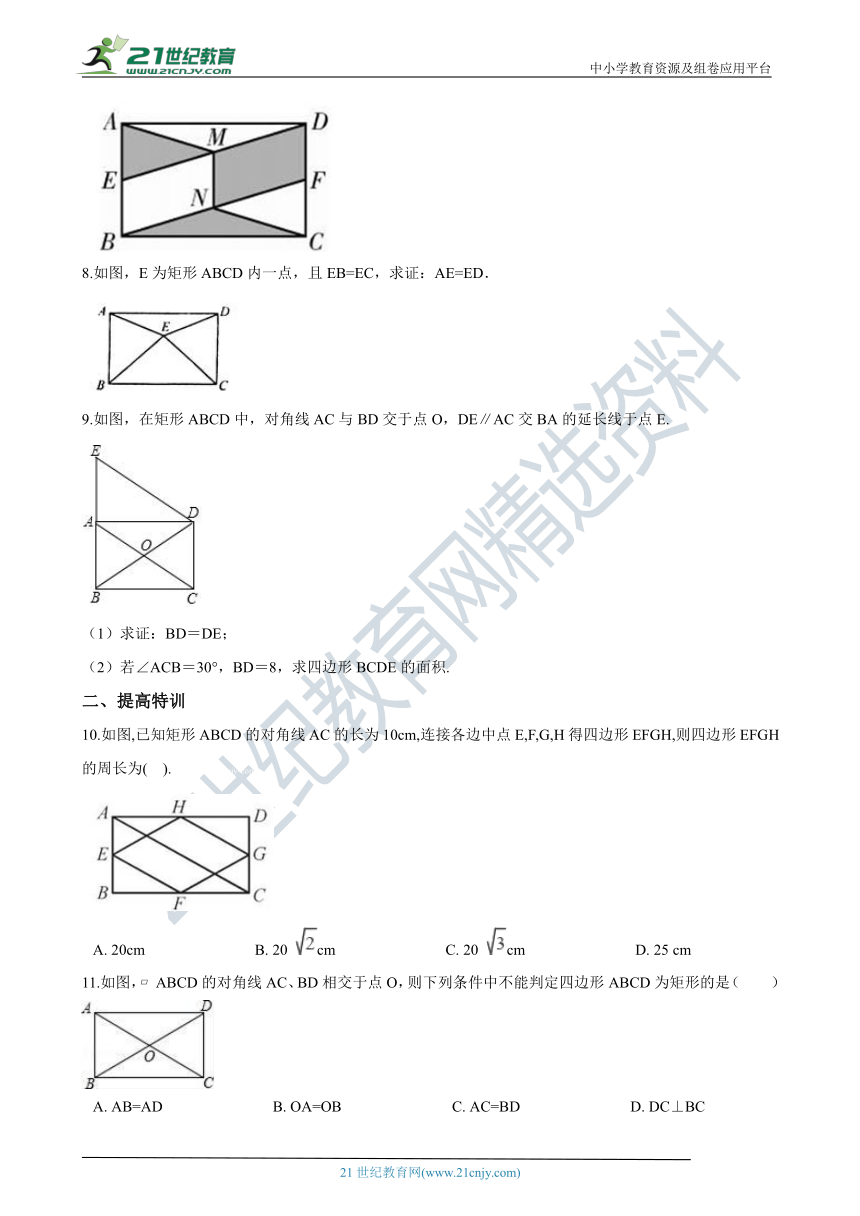
7.如图，矩形ABCD中,点E,F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N,连接AM, CN,MN,若AB=2,BC=3,则图中阴影部分的面积为________. 【来源：21·世纪·教育·网】

8.如图，E为矩形ABCD内一点，且EB=EC，求证：AE=ED．

9.如图，在矩形ABCD中，对角线AC与BD交于点O，DE∥AC交BA的延长线于点E.
（1）求证：BD＝DE；
（2）若∠ACB＝30°，BD＝8，求四边形BCDE的面积.
二、提高特训
10.如图,已知矩形ABCD的对角线AC的长为10cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为(?? ). www-2-1-cnjy-com

A.?20cm?????????????????????????????B.?20 cm?????????????????????????????C.?20 cm?????????????????????????????D.?25 cm
11.如图，?ABCD的对角线AC、BD相交于点O，则下列条件中不能判定四边形ABCD为矩形的是（　　）
A.?AB=AD?????????????????????????????B.?OA=OB?????????????????????????????C.?AC=BD?????????????????????????????D.?DC⊥BC
12.如图，将两根相同的矩形木条沿虚线 剪开得到四根完全一样的木条，然后重新围城一个矩形画框．已知矩形木条的两边分别为 ，且 ，则围城的矩形画框的内框 的面积为（???? ）
A.???????????????B.???????????????C.???????????????D.?
13.如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E.若∠ADE＝22.5°，BD=4，则OE的长为________. 21·世纪*教育网
14.如图，在矩形ABCD中，对角线AC、BD交于点O，DE平分∠ADC.若∠AOB＝60°，则∠COE的大小为________ . 2-1-c-n-j-y
15.如图所示，矩形ABCD的对角线相交于点O，OF⊥AD于点F，OF＝2cm，AE⊥BD于点E，且BE﹕BD＝1﹕4，求AC的长. 21*cnjy*com

答案解析部分
一、基础夯实
1. A
解： ∵A(-2，0)，B(0，1) ∴OA=2，OB=1 在矩形AOBC中，BC=OA=2，AC=OB=1，AC⊥x轴 ∴点C的坐标为（-2，1） 将（-2，1）代入y=kx得：-2k=1 解得：k=-. 【来源：21cnj*y.co*m】
故答案为：A.
【分析】先根据矩形的性质求出点C的坐标，然后用待定系数法求k即可。
2. A
解：∵四边形ABCD是矩形，∴AC=BD，OA=OB，∠OAB=∠OBA=55°，∠AOD=∠OAB+∠OBA=55°+55°=110°. 故答案为：A 【出处：21教育名师】
【分析】由矩形的对角线互相平分得，OA=OB，再由三角形的外角性质得到∠AOD等于∠OAB和∠OBA之和即可求解。【版权所有：21教育】
3. B
解：矩形的性质是对角线互相平分且相等，但不一定互相垂直，只有正方形对角线互相垂直平分且相等，矩形也是轴对称图形，对称轴有两条，即矩形每边的中垂线。 故答案为：B 【分析】根据矩形的性质分析判断，矩形对角线互相平分且相等，其对称轴有两条，即矩形每边的中垂线。21*cnjy*com
4. D
解：∵四边形ABCD为矩形， ∴∠ABC=90°，AC=BD，OA=OB
故答案为：D。
【分析】根据矩形的性质判断即可。
5. C
解：∵四边形ABCD是矩形， ∴AC=BD，OA=OB=OC=OD， ∴∠AOD=2∠BAO=120°， ∴∠BAO=60°，△AOB是等边三角形， ∴AB=AO=AC=2， ∴BC=21世纪教育网版权所有
故答案为：C.
【分析】由矩形的性质得对角线平分且相等，推得△ABC为等边三角形，最后在Rt△ABC中，利用勾股定理即可求得BC的长。
6. 2；4
解：
∵矩形的对角线的夹角是60°
∴较短的边对的三角形是等边三角形
∴这个矩形的较短的边长为2
∴这个矩形较长的边
∴这个矩形的面积
故答案为：2；. 【分析】根据矩形的性质结合对角线的夹角是60°可得较短的边对的三角形是等边三角形，再根据等边三角形的性质结合勾股定理即可求得矩形较长的边，从而求得矩形的面积.
7. 3
解：∵ 点E,F分别是AB,CD的中点 ，M、N分别为DE、BF的中点， ∴矩形绕中心旋转180°阴影部分恰好能够与空白部分重合， ∴阴影部分的面积=空白部分面积=×矩形的面积， ∵AB=2，BC=3， ∴阴影部分的面积=×2×3=3. 故答案为：3.
【分析】根据矩形的中心对称可得阴影部分的面积=空白部分面积=×矩形的面积，利用矩形的面积=长×宽计算即可.
8. 证明：∵矩形ABCD∴∠ABC=∠BCD=90°，AB=CD∵EB=EC，?∴∠EBC=∠ECB，∵∠ABE=90°-∠EBC，∠ECD=90°-∠ECB，?∴∠ABE=∠ECD，在△ABE和△DCE中， ∴△ABE≌△DCE（SAS），?∴AE=ED。
解：根据矩形的性质，易证∠ABC=∠BCD=90°，AB=CD，再根据等腰三角形的性质去证明∠ABE=∠ECD，然后利用SAS证明△ABE≌△DCE，利用全等三角形的性质，可证得结论。
9. （1）证明：∵四边形ABCD是矩形
∴AB＝CD，AC＝BD，AB∥CD，且DE∥AC
∴四边形ACDE是平行四边形
∴DE＝AC
∴DE＝BD
（2）解：∵∠ACB＝30 ，BD＝8＝AC，
∴AB＝4，BC＝ AB＝4
∵四边形ACDE是平行四边形
∴AB＝CD＝AE＝4
∴四边形BCDE的面积＝ ＝24 .
解：（1）由矩形的性质可得AC＝BD，AB∥CD，可证四边形ACDE是平行四边形，可得DE＝AC＝BD；（2）由直角三角形的性质可得AB＝4＝CD＝AE，BC＝4 ，由梯形面积公式可求解.
二、提高特训
10. A
解：如图，连接BD， ∵E、F分别是AB和BC的中点， ∴EF是△ABC的中位线， ∴EF=AC=×10=5cm, 同理HG=EF=5cm， 同理可得，FG=EH=BD， ∵四边形ABCD是矩形， ∴AC=BD， ∴EF=FG=HG=EH=5， ∴ 四边形EFGH的周长为 ：4EF=20cm. 故答案为：A. 21cnjy.com
【分析】因为E,F,G,H是四边形ABCD各边的中点，可得四边形EFGH的各边都是三角形的中位线，结合矩形的对角线相等，可得四边形EFGH的各边长相等，从而求出其周长.21教育名师原创作品
11. A
解：A、不能判定四边形ABCD为矩形，故此选项符合题意；
B、由AO＝BO可证明AC＝BD，能判定四边形ABCD为矩形，故此选项不符合题意；
C、AC＝BD能判定四边形ABCD为矩形，故此选项不符合题意；
D、DC⊥BC能判定四边形ABCD为矩形，故此选项不符合题意；
故答案为：A．
【分析】根据矩形的判定定理：有一个角是直角的平行四边形是矩形，对角线相等的平行四边形是矩形分别进行分析即可．
12. C
解：∵两根相同的矩形木条沿虚线MN剪开得到四根完全一样的木条，矩形木条的两边分别为a，b， 2·1·c·n·j·y
∴CD= ，
∴BC=CD-b= -b= ，
∴矩形ABCD的面积=BC·CD= · ．
故答案为：C．
【分析】结合图形利用矩形的性质求出矩形的长和宽，然后利用矩形的面积公式求解即可．
13.
解：∵四边形ABCD是矩形
∴AO=BO= BD=2，
∵∠ADE＝22.5°，
∴
∵AE⊥BD
∴
∴
∴△AEO是等腰直角三角形，
∴AE=EO
∴AE2+EO2=2EO2= AO2=4
故EO=
故答案为： .
【分析】根据矩形的性质得到 ，由AE⊥BD得到 ，故可知 ，故可得到△AEO是等腰直角三角形，再求出AO=BO= BD=2，故可求出OE的长.
14. 75°
解：∵四边形ABCD是矩形,
∴AO=CO=BO=OD,（矩形的对角线相等且互相平分）
∵∠AOB=60°,
∴∠COD=60°,（对顶角相等）
∴△AOB和△COD为等边三角形,（有一个角是60°的等腰三角形是等边三角形）,?
∴∠BAC=60°,CD=OC,
则∠ACB=30°,（直角三角形两锐角互余）?
∵DE平分∠ADC,
∴∠EDC=45°,
可得△DCE为等腰直角三角形,
∴CD=EC,
∴EC=OC,（等量代换）?
∴∠COE=∠CEO,
∴∠COE=75°（三角形内角和是180°）.
故答案为75°.
【分析】根据四边形ABCD为矩形,利用矩形的对角线互相平分且相等,得到OA=OB=OC=OD,又∠AOB=60°,可得三角形AOB与三角形COD都为等边三角形,进而求出∠ACB为30°,由DE为直角的角平分线,得到∠EDC=45°,可得三角形DEC为等腰直角三角形,即CD=EC,而CD=OC,等量代换可得EC=OC,即三角形OEC为等腰三角形,由顶角∠ACB为30°即可求出底角∠COE的度数.21·cn·jy·com
15. 解：∵四边形ABCD为矩形，
∴∠BAD＝90°，OB＝OD，AC＝BD，
又∵OF⊥AD，
∴OF∥AB，
又∵OB＝OD ，
∴ AB＝2OF＝4cm，
∵BE︰BD＝1︰4，
∴BE︰ED＝1︰3
设BE＝x，ED＝3x ，
则BD＝4 x ，
∵AE⊥BD于点E
∴ ，
∴16－x2＝AD2－9x2
又∵AD2＝BD2－AB2＝16 x2－16 ，
∴16－x2＝16 x2－16－9x2 ， 8x2＝32
∴x2＝4，
∴x＝2
∴BD＝2×4＝8（cm），
∴AC＝8cm .
解：根据矩形的对角线相等且互相平分可得OA=OB，根据比例设BE=x，表示出BD=4x，然后求出BE=OE，从而判断出△ABO是等边三角形，然后判断出OE是△AOD的中位线，根据三角形的中位线平行于第三边并且等于第三边的一半求出AB，再求解即可.www.21-cn-jy.com