5.3 正方形（2） 同步训练（含解析）

初中数学浙教版八年级下册5.3 正方形（2） 同步训练
一、基础夯实
1.正方形具有而菱形不一定具有的性质是(?? ).
A.?四条边都相等???????????B.?对角线互相垂直且平分???????????C.?对角线相等???????????D.?对角线平分一组对角
2.如图,是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是（??? ）． 21cnjy.com
A.?4或6????????????????????????????????????B.?3或5????????????????????????????????????C.?1或7????????????????????????????????????D.?3或6
3.如图，矩形内有两个相邻的正方形，其面积分别为2和8，则图中阴影部分的面积为（??? ）
A.??????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?6
4.如图，四张大小不一的正方形纸片分别放置于矩形的四个角落,其中，①和②纸片既不重叠也无空隙．在矩形ABCD的周长己知的情况下，知道下列哪个正方形的边长，就可以求得阴影部分的周长（ ??）
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
5.如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的?ALMN，若中间空白部分四边形OPQR恰好是正方形，且?ALMN的面积为50，则正方形EFGH的面积为（?? ）
A.?24?????????????????????????????????????????B.?25?????????????????????????????????????????C.?26?????????????????????????????????????????D.?27
6.如果正方形的对角线长为 ，那么这个正方形的面积为________.
7.如图，点E在正方形ABCD的边BA的延长线上，连接AC，AC＝AE，CE交AD于点F，则∠ACE的度数等于________. 21教育网
8.如图，正方形ABCD的对角线AC，BD相交于点O.E，G分别是OB，OC上的点，CE与DG的延长线相交于点F.若DF⊥CE，求证：OG＝OE. 2·1·c·n·j·y
9.如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1 ， 点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为 S2 ， 且S1=S2. 21·世纪*教育网

（1）求线段CE的长.
（2）若点日为BC边的中点，连接HD，求证：HD=HG.
二、提高特训
10.如图，四边形ABCD是正方形，直线L1、L2、L3 ， 若L1与L2的距离为5，L2与L3的距离7，则正方形ABCD的面积等于（? ?） www-2-1-cnjy-com
A.?70???????????????????????????????????????B.?74???????????????????????????????????????C.?144???????????????????????????????????????D.?148
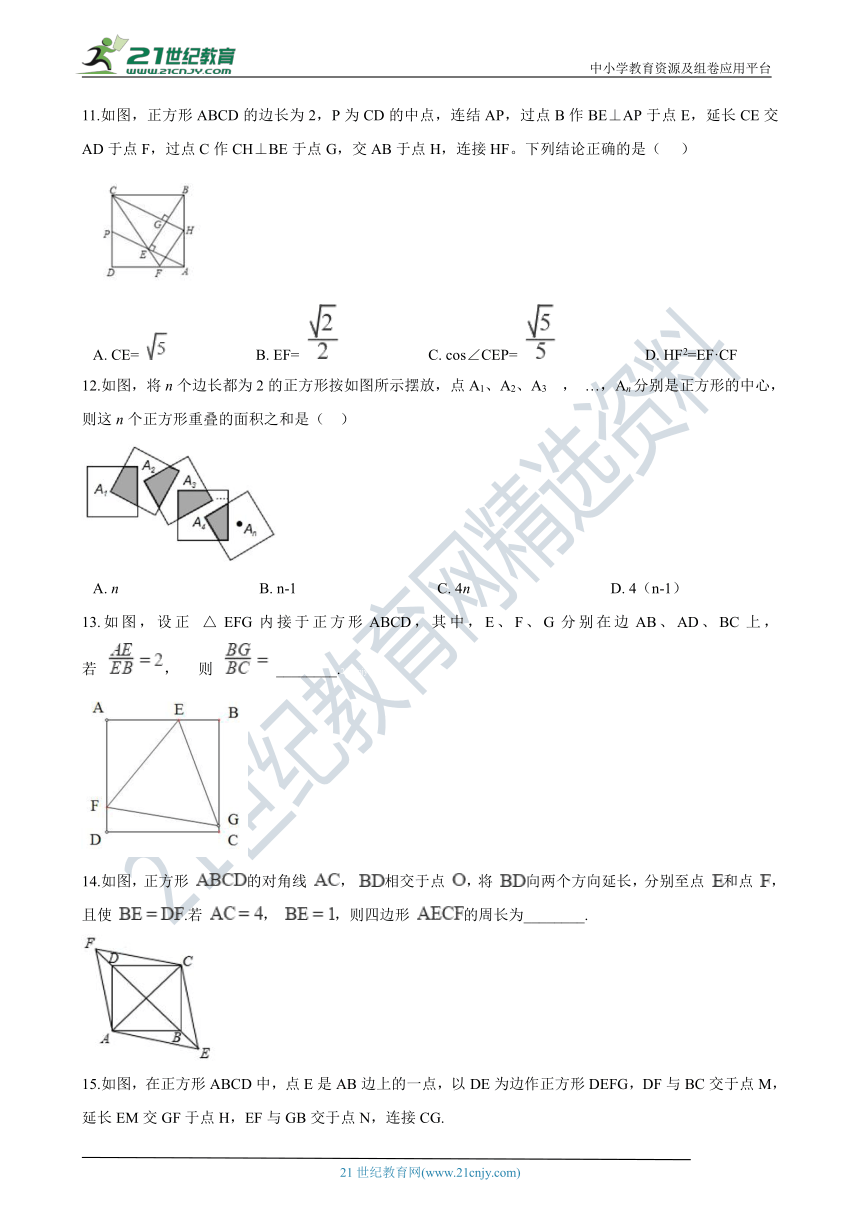
11.如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF。下列结论正确的是（ ???）

A.?CE= ???????????????????????B.?EF= ???????????????????????C.?cos∠CEP= ???????????????????????D.?HF2=EF·CF
12.如图，将n个边长都为2的正方形按如图所示摆放，点A1、A2、A3 ， …，An分别是正方形的中心，则这n个正方形重叠的面积之和是（?? ） 2-1-c-n-j-y
A.?n?????????????????????????????????????B.?n-1?????????????????????????????????????C.?4n?????????????????????????????????????D.?4（n-1）
13.如图，设正 △ EFG内接于正方形ABCD，其中，E、F、G分别在边AB、AD、BC上，若? ， ? 则? ?________.21*cnjy*com
14.如图，正方形 的对角线 ， 相交于点 ，将 向两个方向延长，分别至点 和点 ，且使 .若 ， ，则四边形 的周长为________. 【出处：21教育名师】
15.如图，在正方形ABCD中，点E是AB边上的一点，以DE为边作正方形DEFG，DF与BC交于点M，延长EM交GF于点H，EF与GB交于点N，连接CG. 【版权所有：21教育】
（1）求证：CD⊥CG；
（2）若tan∠MEN= ，求 的值；
（3）已知正方形ABCD的边长为1，点E在运动过程中，EM的长能否为 ？请说明理由.

答案解析部分
一、基础夯实
1. C
解：A、正方形和菱形的四条边都相等，故A不合题意； B、正方形和菱形的对角线都互相垂直且平分，故B不合题意； C、正方形的对角线相等，菱形的对角线不相等，故C合题意； D、正方形和菱形的对角线都平分一组对角，故D不合题意； 故选：C. 21·cn·jy·com
【分析】正方形的四条边相等，对角线互相垂直、平分、相等，且对角线平分一组对角；菱形的四条边相等，对角线互相垂直平分且平分一组对角，据此逐一判断即可.www.21-cn-jy.com
2. D
解：如图，延长BD.AF交于点E，延长BM,AN交于点C
根据题意可知：EF=3；CM=9-x且四边形EACB为矩形
∵若直线AB将它分成面积相等的两部分，
∴矩形EFGD与矩形HNCM的面积相等
∴?? x(9-x)=6×3
? x2-9x+18=0
解得：x=3，或x=6，
故答案为：D．
【分析】如图，延长BD.AF交于点E，延长BM,AN交于点C，根据正方形的性质及矩形的性质可以得出EF,的长，进而即可表示出CM的长，进而再根据矩形的一条对角线，将矩形分割成两面积相等的三角形，从而即可题意即可得出矩形EFGD与矩形HNCM的面积相等，根据矩形的面积计算方法列出方程，求解即可.【来源：21·世纪·教育·网】
3. B
解：由题意可得，大正方形的边长为 ，小正方形的边长为 ，
∴图中阴影部分的面积为： ，
故答案为：B．
【分析】根据正方形的性质可求出大正方形的边长及小正方形的边长，图中阴影部分利用平移可得一个矩形，利用矩形的面积公式计算即可.21教育名师原创作品
4. B
解：设正方形①的边长为a，正方形②的边长为b，正方形③的边长为c，正方形④的边长为d ∵ABCD是矩形， ∴AB=CD=a+b，AD=BC ∴AB+a-b+BC-b-c+2c+AB-c-d+2d+BC-a-d =2AB+2BC-2b ∴在矩形ABCD的周长己知的情况下，只需知道正方形②的边长，就可求出阴影部分的面积， 故答案为：B 【分析】设正方形①的边长为a，正方形②的边长为b，正方形③的边长为c，正方形④的边长为d，利用矩形的的对边相等，正方形的四边相等，就可列出阴影部分的周长，再化简就可求出结果。
5. B
解：设EF=a，BC=b，AB=c，则PQ=a-c，RQ=b-a，PQ=RQ
∴a= ，
∵?ALMN的面积为50，∴bc+a2+(a-c)2=50,
把a= 代入化简求值得b+c=10, ∴a=5,
∴正方形EFGH的边长为5，
∴正方形EFGH的面积为25，
故答案为：B.
【分析】此题涉及的知识点是正方形、长方形的性质，先根据正方形和长方形的性质求出各边长的关系，再根据?ALMN的面积，求出各边长的关系，最后得出面积.
6. 1
解：正方形的面积= .
故答案为：1.
【分析】根据正方形的面积等于对角线乘积的一半求解即可.
7. 22.5°
解：∵AC＝AE，
∴∠E＝∠ACE，
∵AC是正方形ABCD的对角线，
∴∠BAD＝90 ，∠BAC＝45 ，
∴∠E+∠ACE＝45 ，
∴∠ACE＝ ×45 ＝22.5 ，
故答案为：22.5 .
【分析】根据等边对等角的性质可得∠E＝∠ACE，由正方形的性质得出∠BAC＝45 ，再由三角形的外角性质即可得出结果.
8. 证明：∵四边形ABCD是正方形，∴AC⊥BD，OC=OD，∴∠DOG=∠EOC=90°，∠OCE+∠CED=90°∵DF⊥CE，∴∠EDF+∠CED=90°∴∠EDF=∠OEC∴△DOG≌△COE（ASA）∴OE=OG
解：由四边形ABCD是正方形，对角线互相垂直且互相平分，可知角DOG等于角EOC，DO等于CO，再由已知条件给出的DF与CE垂直，可知角EDF与角DEF互余，这样根据同角的余角相等，可以得到角ODG与角OCE相等，即可证得△DOG与△EOC全等，由全等三角形的对应边相等，可证OG=OE。
9. （1）解：根据题意，得AD=BC=CD=1，∠BCD=90°.
设CE=x（0因为S1=S2 ， 所以x2=1-x，
解得x= （负根舍去），
即CE= .
（2）证明：因为点日为BC边的中点，
所以CH= ，所以HD= ，
因为CG=CE= ，点H，C，G在同一直线上，
所以HG=HC+CG= + = ，所以HD=HG
解：（1）由正方形性质得AD=BC=CD=1，∠BCD=90°，CE=CG，设小正方形边长CE=x，则DE=1-x，由S1=S2列出方程，解之即可求得答案.（2）由中点定义得CH= ，在Rt△DHC中，根据勾股定理求得HD= ，再由HG=HC+CG= ，即HD=HG.
二、提高特训
10. B
解：如下图，过点A作AE⊥l2于点E，过点C作CF⊥l2于点F， 由辅助线得，∠CBF+∠BCF=90°. ∵四边形ABCD是正方形， ∴AB=BC=CD=AD，∠DAB=∠ABC=∠BCD=∠CDA=90° ∴∠CBF+∠ABE=90°， ∴∠ABE=∠BCF. 在△ABE和△BCF中， ， ∴△ABE≌△BCF（AAS）， ∴AE=BF. 由辅助线得，l1到l2 ， l2到l3的距离分别是线段AE、CF的长， ∴在Rt△BFC中，BC2=BF2+CF2 ， 即：BC2=52+72=74. 即：正方形ABCD的面积是74. 故答案为：B. 【分析】过点A作AE⊥l2于点E，过点C作CF⊥l2于点F，即线段AE、CF的长分别是l1到l2 ， l2到l3的距离，通过证明△ABE≌△BCF，得出BF=AE，再根据勾股定理进而得出正方形ABCD的面积即可.
11. D
解：连接EH。 在正方形ABCD中，∠D=∠ABC=90°，AB∥CD，AB=BC=CD=AD=2
∵P为CD的中点 ∴PC= 又∵?AP⊥BE，CH⊥BE? ?∴AP∥CH ∴四边形APCH是平行四边形? ? ?∴AH=PC=1 ∴BH=AH=1 在Rt△ABE中，EH=BH 又∵?CH⊥BE? ∴BH=EH= ∴CH是BE的垂直平分线 ∴CE=BC=2，故A错误； ∵CE=CB，CH=CH，EH=BH ∴△CEH≌△CBH ∴∠CEB=∠ABC=90° 又∵EH=AH=1，FH=FH ∴Rt△EFH≌△Rt△AFH ∴AF=EF 设EF=AF=x 在Rt△CDF中，由勾股定理得：CD2+DF2=CF2 ， 即，22+（2-x）2=（2+x）2 解得 x=? ?∴EF=， 故B错误； 在Rt△CEH中，CH=?,∴cos∠ECH= ∵AP∥CH? ∴∠CEP=∠ECH? ，∴cos∠CEP=cos∠ECH=,故C错误； 在Rt△AFH中，HF2=AF2+AH2=（）2+1= EF·CF=×（2+）= ∴HF2=EF·CF，故D正确。 故答案为：D.【来源：21cnj*y.co*m】
【分析】先判断四边形APCH是平行四边形，再利用平行四边形的性质、中点的定义以及直角三角形斜边中线的性质得AH=BH=EH，然后利用线段的垂直平分线的判定和性质得CE=BE，然后在证得△CEH≌△CBH、Rt△EFH≌△Rt△AFH，利用全等三角形的性质及勾股定理即可对各个选项一一作出判断。
12. B
解：
如图示，由分别过点A1、A2、A3 ， 垂直于两边的垂线，由图形的割补可知：一个阴影部分面积等于正方形面积的 ，即阴影部分的面积是 ，21*cnjy*com
n个这样的正方形重叠部分（阴影部分）的面积和为： ．
故答案为：B．
【分析】根据题意可得，阴影部分的面积是正方形的面积的 ，已知两个正方形可得到一个阴影部分，则n个这样的正方形重叠部分即为（n-1）个阴影部分的和．
13.
解：如图，过点E作EK⊥FG于点K，K是FG的中点，连接AK、KB， 易知E、K、G、B和E、K、F、A分别四点共圆. ∴∠KBE=∠EGK=60°，∠EAK=∠EFK=60°. ∴△ABK是等边三角形. 过点K作KM⊥AB于点M，M是AB的中点，设AB=6， ∴EB=AB=2，MB=3，ME=1，MK=6sin60°=， EK==， EG==， BG==. ∴=. 故答案为：. 【分析】作出辅助线，可知△ABK是等边三角形. 设出正方形的边长，这里设正方形的边长为6主要是①本题是选择题；②考虑后续便于计算，解直角三角形求出BG，再计算比值.
14.
解：设AC与BD交于点O，
∵四边形ABCD是正方形，
∴AO＝CO＝BO＝DO＝2，AC⊥BD，??
∵BE＝DF＝1，
∴OE＝OF＝3，且OA＝OC，
∴四边形AECF是平行四边形，
又∵AC⊥BD
∴四边形AECF是菱形
∴AE＝CE＝CF＝AF，
在Rt△COE中，CE＝ ＝ ＝
∴四边形AECF的周长为4
故答案为：4 .
【分析】设AC与BD交于点O，利用正方形的对角线的性质，可证AO＝CO＝BO＝DO＝2，AC⊥BD，再利用已知BE=DF，可证得OE=OF，利用对角线互相平分的四边形是平行四边形，可证四边形AECF是平行四边形，再利用对角线互相垂直的平行四边形是菱形，易证四边形AECF是菱形，根据菱形的性质，可知AE=CE=CF=EF，然后利用勾股定理求出CE的长，即可得到四边形AEF的周长。
15. （1）证明：∵四边形ABCD和四边形DEFG是正方形，
∴∠A=∠ADC=∠EDG=90°，AD=CD，DE=DG，
∴∠ADE=∠CDG，
在△ADE和△CDG中，
∴△ADE≌△CDG（SAS），
∴∠A=∠DCG=90°，
∴CD⊥CG；（2）解：
∵CD⊥CG，DC⊥BC，
∴G、C、M三点共线
∵四边形DEFG是正方形，
∴DG=DE，∠EDM=∠GDM=45°，
又∵DM=DM
∴△EDM≌△GDM，
∴∠DME=∠DMG
又∠DMG=∠NMF，
∴∠DME=∠NMF，
又∵∠EDM=∠NFM=45°
∴△DME∽△FMN，
∴
又∵DE∥HF，
∴ ，
又∵ED=EF，
∴
在Rt△EFH中，tan∠HEF= ，
∴
（3）解：EM的长不可能为 。
理由：假设EM的长为 ，
∵点E是AB边上一点，且∠EDG=∠ADC=90°，
∴点G在BC的延长线上，
同（2）的方法得，EM=GM= ，
∴GM= ，
在Rt△BEM中，EM是斜边，
∴BM＜
∵正方形ABCD的边长为1，
∴BC=1，
∴CM＞
∴CM＞GM，
∴点G在正方形ABCD的边BC上，与“点G在BC的延长线上”相矛盾，
∴假设错误，
即：EM的长不可能为
解：（1）根据正方形的性质得出∠A=∠ADC=∠EDG=90°，AD=CD，DE=DG，继而得出∠ADE=∠CDG，由SAS证明△ADE≌△CDG，然后根据全等三角形的性质得出∠A=∠DCG=90°，即可得证； （2）先由CD⊥CG，DC⊥BC判断出G、C、M三点共线，然后利用正方形的性质易得△EDM≌△GDM，根据全等三角形的性质得出∠DME=∠DMG，而∠DMG=∠NMF，等量代换得到∠DME=∠NMF，继而可证明△DME∽△FMN，得出 ?；由DE∥HF，得出 ， 由ED=EF等量代换得 ?。在Rt△EFH中，tan∠HEF= ， 所以 ； （3）假设EM= ?。同（2）得EM=GM= ?；在Rt△BEM中判断出BM＜ ，得出CM＞ ，进而得出CM＞GM，推出矛盾，假设不成立，即可得出结论．21世纪教育网版权所有