第五章 特殊平行四边形中档检测试题(含答案)
文档属性
| 名称 | 第五章 特殊平行四边形中档检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-10 15:30:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学四边形(含特殊四边形)中考中高档题
——选自中考数学
客观题:
1.如图,在?ABCD中,点E是DC边上一点,连接AE、BE,若AE、BE分别是∠DAB、∠CBA的角平分线,且AB=4,则?ABCD的周长为( )
A.10 B. C. D.12
2.如图,一块呈平行四边形的菜地,被分割成3个菱形和2个平行四边形后仍是中心对称图形.若只知道原平行四边形菜地的周长,则不用测量就能知道分割后的图形的周长的图形标号为( )
A.①②③ B.①② C.②③ D.①③
3.如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O.已知下列选项,能得到图中阴影部分面积的是( )
A.平行四边形ABCD的面积 B.梯形AOCD的面积
C.平行四边形EFGH的面积的一半 D.梯形EOGF的面积
4.如图,四边形为菱形,,两点的坐标分别是,,点,在坐标轴上,则菱形的周长等于
A. B. C. D.20
5.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A.0 B.4 C.6 D.8
6.如图,正方形纸片的边长为12,是边上一点,连接.折叠该纸片,使点落在上的点,并使折痕经过点,得到折痕,点在上.若,则的长为__________.
7.如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为点,D点的对称点为点,若,的面积为4,的面积为1,则矩形ABCD的面积等于__________.
8.将边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置(如图),使得点D落在对角线CF上,EF与AD相交于点H,则HD= .(结果保留根号)
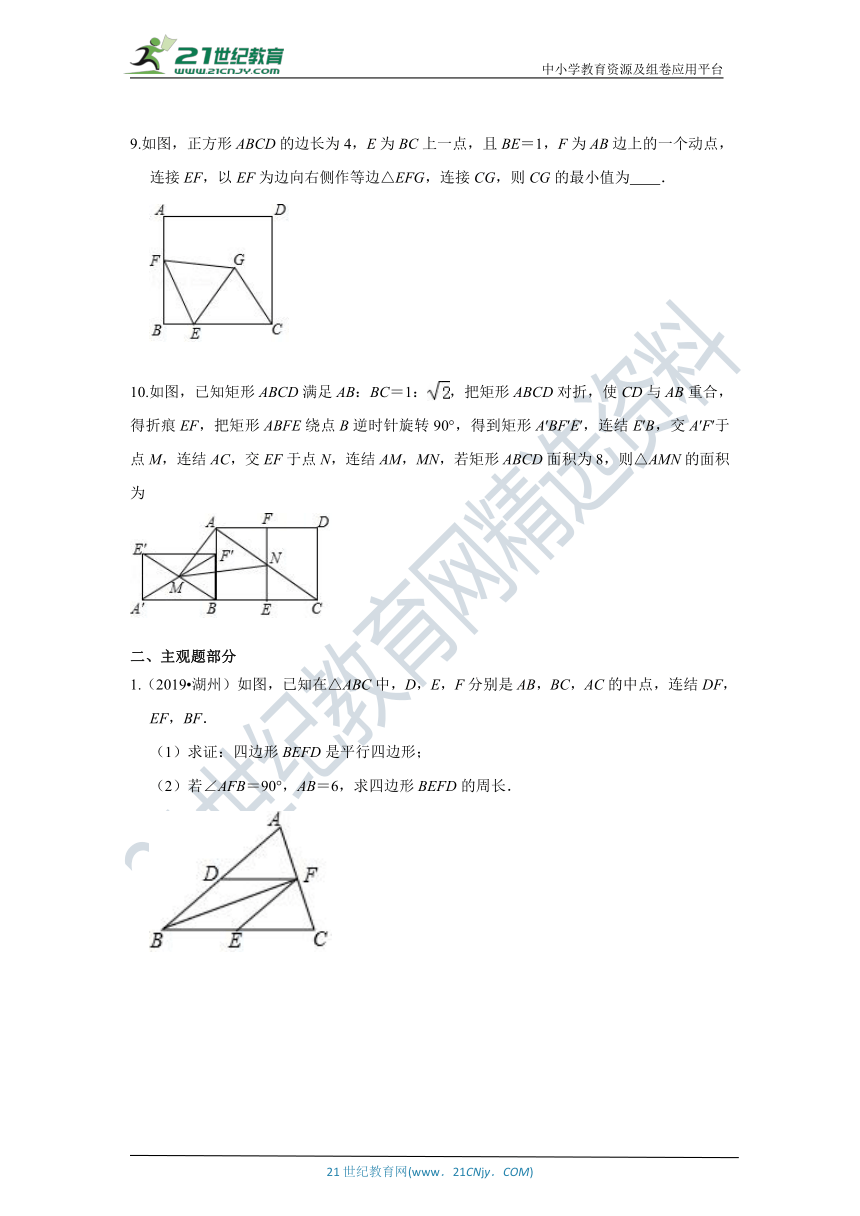
9.如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
10.如图,已知矩形ABCD满足AB:BC=1:,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为
主观题部分
1.(2019?湖州)如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.
(1)求证:四边形BEFD是平行四边形;
(2)若∠AFB=90°,AB=6,求四边形BEFD的周长.
2.(2019?宁波)如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
3.(2019?衢州)如图,在4×4的方格子中,△ABC的三个顶点都在格点上.
(1)在图1中画出线段CD,使CD⊥CB,其中D是格点.
(2)在图2中画出平行四边形ABEC,其中E是格点.
4.(2019?徐州)如图,将平行四边形纸片ABCD沿一条直线折叠,使点A与点C重合,点D落在点G处,折痕为EF.求证:
(1)∠ECB=∠FCG;
(2)△EBC≌△FGC.
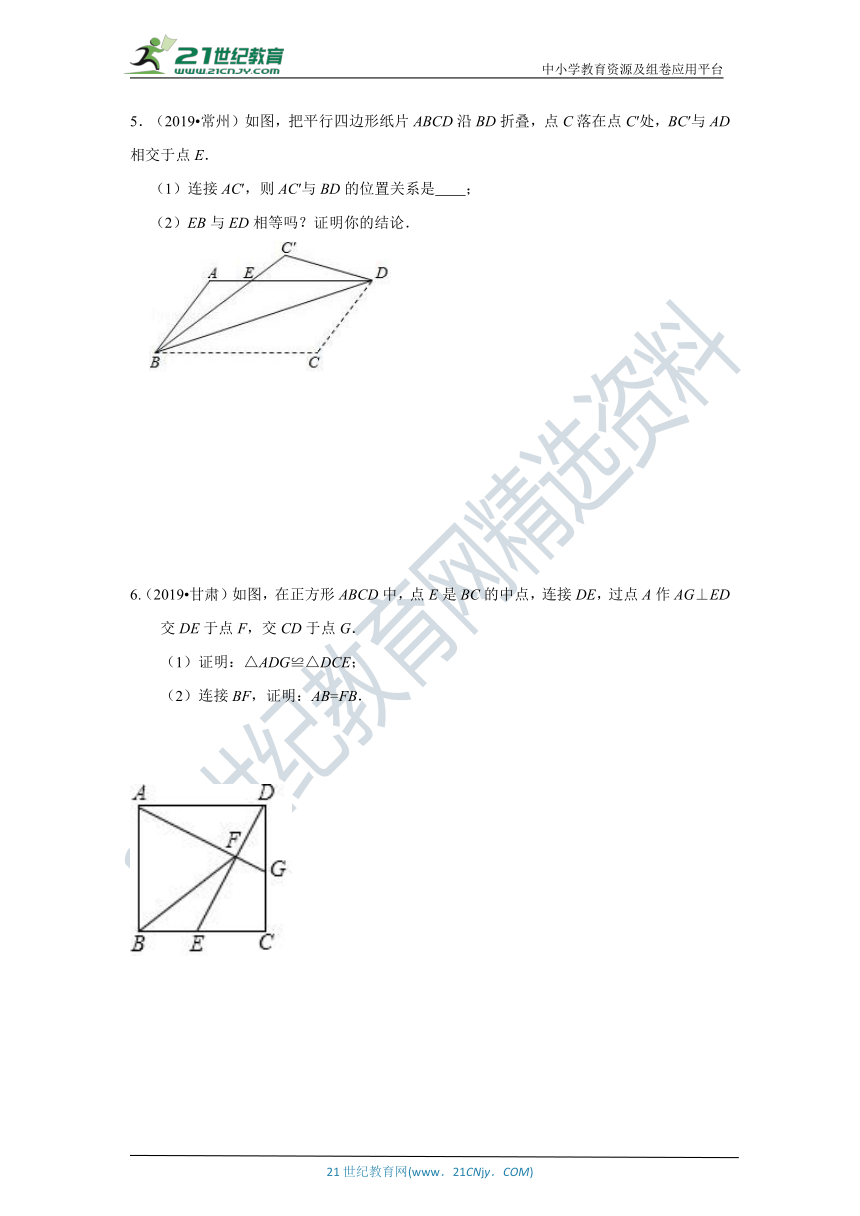
5.(2019?常州)如图,把平行四边形纸片ABCD沿BD折叠,点C落在点C′处,BC′与AD相交于点E.
(1)连接AC′,则AC′与BD的位置关系是 ;
(2)EB与ED相等吗?证明你的结论.
6.(2019?甘肃)如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,证明:AB=FB.
7.(2019·安徽)如图,点E在ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF;
(2)设ABCD的面积为S,四边形AEDF的面积为T,求的值.
8.(2019·山东滨州)如图,矩形中,点在边上,将沿折叠,点落在边上的点处,过点作交于点,连接.
(1)求证:四边形是菱形;
(2)若,求四边形的面积.
9.(2019·杭州)如图,已知正方形ABCD的边长为1,正方形CEFG的面积为,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为,且.
(1)求线段CE的长;
(2)若点H为BC边的中点,连结HD,求证:.
10.(2019?宁波)定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.
求证:四边形ABEF是邻余四边形.
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上.
(3)如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.
答案
客观题部分
D 2.C 3.C 4.C 5.D
7. 8. 9. 10.2
主观题部分
1.【答案】(1)证明:∵D,E,F分别是AB,BC,AC的中点,
∴DF∥BC,EF∥AB,
∴DF∥BE,EF∥BD,
∴四边形BEFD是平行四边形;
(2)解:∵∠AFB=90°,D是AB的中点,AB=6,
∴DF=DB=DA=AB=3,
∵四边形BEFD是平行四边形,
∴四边形BEFD是菱形,
∵DB=3,
∴四边形BEFD的周长为12.
2.【答案】解:(1)∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°﹣∠GFH,∠DHE=180°﹣∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
(2)连接EG,
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE∥BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.
3.【答案】解:(1)线段CD即为所求.
(2)平行四边形ABEC即为所求.
【点睛】本题考查作图﹣应用与设计,平行四边形的判定等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
4.【答案】证明:(1)∵四边形ABCD是平行四边形,
∴∠A=∠BCD,
由折叠可得,∠A=∠ECG,
∴∠BCD=∠ECG,
∴∠BCD﹣∠ECF=∠ECG﹣∠ECF,
∴∠ECB=∠FCG;
(2)∵四边形ABCD是平行四边形,
∴∠D=∠B,AD=BC,
由折叠可得,∠D=∠G,AD=CG,
∴∠B=∠G,BC=CG,
又∵∠ECB=∠FCG,
∴△EBC≌△FGC(ASA).
【点睛】本题主要考查了平行四边形的性质,平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.
5.【答案】解:(1)连接AC′,则AC′与BD的位置关系是AC′∥BD,
故答案为:AC′∥BD;
(2)EB与ED相等.
由折叠可得,∠CBD=∠C'BD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE.
6.【答案】(1)见解析;(2)见解析.
【解析】(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
(2)如图,延长DE交AB的延长线于H,
∵E是BC的中点,∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,即B是AH的中点,
又∵∠AFH=90°,∴Rt△AFH中,BF=AH=AB.
7.【答案】(1)证明略;(2)=2.
【解析】(1)∵四边形ABCD为平行四边形,∴,
,
又,
,
,
,
同理可得:,
在和中,,
∴△BCE≌△ADF;
(2)连接EF,
∵△BCE≌△ADF,,
又,
∴四边形ABEF,四边形CDFE为平行四边形,
∴,
∴,
设点E到AB的距离为h1,到CD的距离为h2,线段AB到CD的距离为h,
则h=h1+h2,
∴,即=2.
8.【答案】(1)详见解析;(2).
【解析】(1)由题意可得,,
∴,
∵,∴,
∴,∴,∴,
∴四边形是平行四边形,
又∵∴四边形是菱形;
(2)∵矩形中, ,
∴,
∴,∴,
设,则,
∵,∴,解得,
∴,∴四边形的面积是:.
9.【答案】(1)CE=;(2)见解析.
【解析】根据题意,得AD=BC=CD=1,∠BCD=90°.
(1)设CE=x(0
解得x=(负根已舍去),即CE=.
(2)因为点H为BC边的中点,
所以CH=,所以HD=,因为CG=CE=,点H,C,G在同一直线上,
所以HG=HC+CG=+=,所以HD=HG.
【名师点睛】本题考查正方形的性质、勾股定理和一元二次方程,解题的关键是根据题意列出一元二次方程.
10.【答案】解:(1)∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,∴∠ADB=90°,∴∠DAB+∠DBA=90°,
∠FAB与∠EBA互余,
∴四边形ABEF是邻余四边形;
(2)如图所示(答案不唯一),
四边形AFEB为所求;
(3)∵AB=AC,AD是△ABC的角平分线,∴BD=CD,
∵DE=2BE,∴BD=CD=3BE,∴CE=CD+DE=5BE,
∵∠EDF=90°,点M是EF的中点,
∴DM=ME,∴∠MDE=∠MED,∵AB=AC,
∴∠B=∠C,∴△DBQ∽△ECN,∴,
∵QB=3,∴NC=5,∵AN=CN,∴AC=2CN=10,∴AB=AC=10.
21世纪教育网 www.21CNjy.COM 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21CNjy.COM)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
