浙教版九年级数学上册3.4:圆心角说课课件(共23张ppt)
文档属性
| 名称 | 浙教版九年级数学上册3.4:圆心角说课课件(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 459.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 15:22:04 | ||
图片预览



文档简介
(共23张PPT)
勤慎诚恕 博雅精进
3.4 圆心角
制作人:叶珏玲
A
B
C
D
教材分析
学情分析
教法分析
教学过程
课后反思
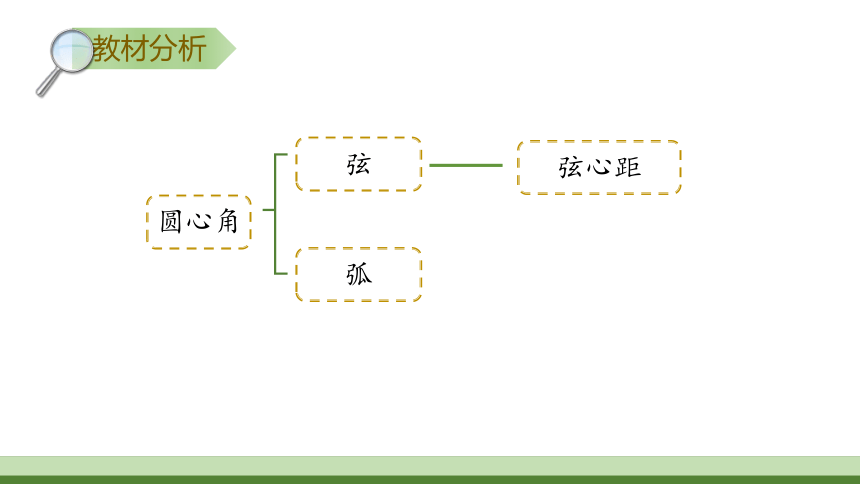
教材分析
弧
圆心角
弦
弦心距
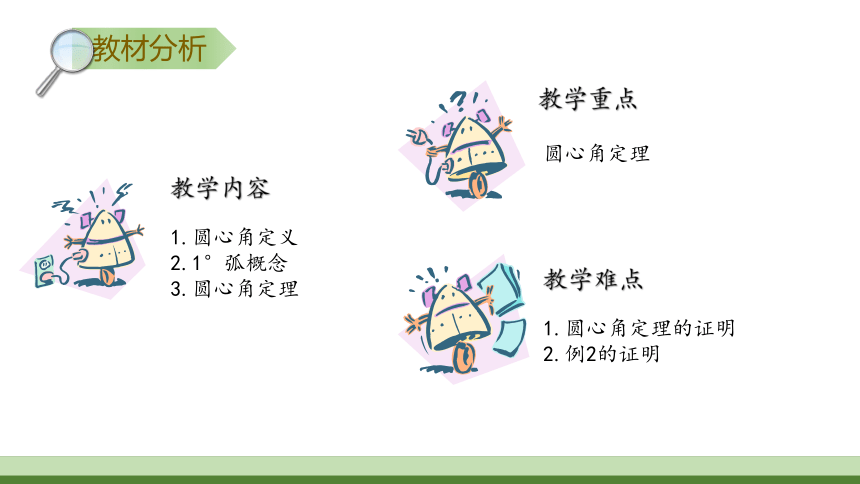
教材分析
教学内容
1.圆心角定义
2.1°弧概念
3.圆心角定理
教学重点
圆心角定理
教学难点
1.圆心角定理的证明
2.例2的证明
知识技能
教学目标
数学思考
1.体会圆的旋转不变性
2.理解圆心角的定义
3.掌握圆心角定理
4.能够利用学过的知识证明:在同圆或等圆中,相同的圆心角所对的两条弦心距相等。
1.经历圆心角定理的探索、证明、应用的过程,养成自主探究、合作交流的学习习惯。
1.体会类比、分类的数学思想方法。
问题解决
通过相关的证明或计算题目的训练,提高学生运用所学知识解决实际问题的能力
情感态度
1.发展合情推理能力,逻辑思维能力和推理论证的表达能力
2.体验实现价值后的快乐,锻炼锲而不舍的意志。
学情分析
情感储备:
知识储备:
1.图形的对称及旋转
2.圆的基础概念
3.垂径定理
1.较不活泼好动且积极性较低
2.吸收新知识新概念快
3.思维抽象能力差
教法分析
探究活动
引导者
组织者
合作者
教 师
学习主体
参与者
学 生
教法分析
强调学生的主体性
强调学生的发展性
强调教育的情感性
导
探
练
结
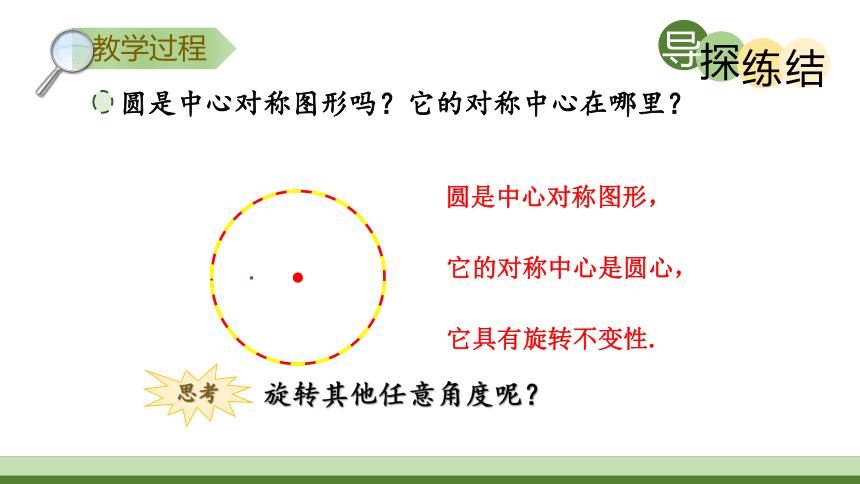
圆是中心对称图形吗?它的对称中心在哪里?
教学过程
思考
旋转其他任意角度呢?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
导
探
练
结
教学过程
N
0°
O
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
15°
N′
15°
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
30°
N′
30°
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
60°
N′
60°
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
n°
N′
由此可以看出,点 N′仍落在圆上.
n°
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆重合.
我们把顶点在圆心的角叫做圆心角.如∠NON′是圆 O 的一个圆心角.
导
探
练
结
圆心角的判别
教学过程
①
②
③
④
教学过程
合作学习
如图1:在圆O中,已知圆心角∠AOB和圆心角∠COD相等。
设计一个实验,探索两个相等的圆心角所对的两段弧,两条弦之间有什么关系?
怎么证明?
导
探
练
结
猜想:
。
导
探
练
结
教学过程
特点:
1.无限
2.不循环
提出问题:如何用数学语言证明这个猜想呢?
已知:如图1,在圆中,已知圆心角和圆心角相等。求证:,。
证明:设,
因为,
所以.
将扇形按顺时针方向旋转角后,点与点重合,点与点也重合。根据圆的旋转性质,重合,重合。所以,。
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
定理深析
教学过程
定理“在同圆和等圆中,相等的圆心角所对的弧相等, 所对的弦也相等”中, 可否把条件“在同圆或等圆中”去掉?为什么?
如图,虽然∠AOB=∠A′O′B′,但AB≠A′B′, 。
导
探
练
结
教学过程
导
探
练
结
把圆心角等分成 360 份,则每一份的圆心角是 1°,
同时整个圆也被分成了 360 份.
则每一份这样的弧叫做 1°的弧.
1°的圆心角对着 1°的弧,
1°的弧对着 1°的圆心角.
n°的圆心角对着 n°的弧,
n°的弧对着 n°的圆心角.
性质:
弧的度数和它所对圆
心角的度数相等.
这样,
1°的弧
1°
n°的弧
n°
教学过程
导
探
练
结
任意画两个半径不相等的圆,然后在每一个圆上任意取一段的弧,这个两段弧的度数相等吗?能说这两段弧相等吗?为什么?
辩
辩
一
做一做:
如图2,在圆O中,∠AOB=135°,求的度数
区别弧和弧的度数
例题讲解
教学过程
导
探
练
结
例1 用直尺和圆规把圆四等分。
例2 证明:在同圆或等圆中,相等的圆心角所对的两条弦的弦心距相等。
已知:图3,在圆中,,OE是弦AB的弦心距,OF是弦CD的弦心距。证明:OE=OF。
证明:
(圆心角定理).
(垂径定理)
同理,,所以,
教学过程
导
探
练
结
(五)总结提升,打下伏笔
1、圆心角:顶点在圆心的角。
2、圆是中心对称图形,圆心是它的对称中心。
3、圆具有旋转不变性。
4、圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。所对的弦心距也相等。
5、弧的度数和它所对圆心角的度数相等。
弧
圆心角
弦
弦心距
补充说明
作业布置
板书设计
课内练习1,2题;作业题2,4题。
勤慎诚恕 博雅精进
3.4 圆心角
制作人:叶珏玲
A
B
C
D
教材分析
学情分析
教法分析
教学过程
课后反思
教材分析
弧
圆心角
弦
弦心距
教材分析
教学内容
1.圆心角定义
2.1°弧概念
3.圆心角定理
教学重点
圆心角定理
教学难点
1.圆心角定理的证明
2.例2的证明
知识技能
教学目标
数学思考
1.体会圆的旋转不变性
2.理解圆心角的定义
3.掌握圆心角定理
4.能够利用学过的知识证明:在同圆或等圆中,相同的圆心角所对的两条弦心距相等。
1.经历圆心角定理的探索、证明、应用的过程,养成自主探究、合作交流的学习习惯。
1.体会类比、分类的数学思想方法。
问题解决
通过相关的证明或计算题目的训练,提高学生运用所学知识解决实际问题的能力
情感态度
1.发展合情推理能力,逻辑思维能力和推理论证的表达能力
2.体验实现价值后的快乐,锻炼锲而不舍的意志。
学情分析
情感储备:
知识储备:
1.图形的对称及旋转
2.圆的基础概念
3.垂径定理
1.较不活泼好动且积极性较低
2.吸收新知识新概念快
3.思维抽象能力差
教法分析
探究活动
引导者
组织者
合作者
教 师
学习主体
参与者
学 生
教法分析
强调学生的主体性
强调学生的发展性
强调教育的情感性
导
探
练
结
圆是中心对称图形吗?它的对称中心在哪里?
教学过程
思考
旋转其他任意角度呢?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
导
探
练
结
教学过程
N
0°
O
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
15°
N′
15°
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
30°
N′
30°
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
60°
N′
60°
导
探
练
结
教学过程
把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.
N
O
n°
N′
由此可以看出,点 N′仍落在圆上.
n°
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆重合.
我们把顶点在圆心的角叫做圆心角.如∠NON′是圆 O 的一个圆心角.
导
探
练
结
圆心角的判别
教学过程
①
②
③
④
教学过程
合作学习
如图1:在圆O中,已知圆心角∠AOB和圆心角∠COD相等。
设计一个实验,探索两个相等的圆心角所对的两段弧,两条弦之间有什么关系?
怎么证明?
导
探
练
结
猜想:
。
导
探
练
结
教学过程
特点:
1.无限
2.不循环
提出问题:如何用数学语言证明这个猜想呢?
已知:如图1,在圆中,已知圆心角和圆心角相等。求证:,。
证明:设,
因为,
所以.
将扇形按顺时针方向旋转角后,点与点重合,点与点也重合。根据圆的旋转性质,重合,重合。所以,。
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
定理深析
教学过程
定理“在同圆和等圆中,相等的圆心角所对的弧相等, 所对的弦也相等”中, 可否把条件“在同圆或等圆中”去掉?为什么?
如图,虽然∠AOB=∠A′O′B′,但AB≠A′B′, 。
导
探
练
结
教学过程
导
探
练
结
把圆心角等分成 360 份,则每一份的圆心角是 1°,
同时整个圆也被分成了 360 份.
则每一份这样的弧叫做 1°的弧.
1°的圆心角对着 1°的弧,
1°的弧对着 1°的圆心角.
n°的圆心角对着 n°的弧,
n°的弧对着 n°的圆心角.
性质:
弧的度数和它所对圆
心角的度数相等.
这样,
1°的弧
1°
n°的弧
n°
教学过程
导
探
练
结
任意画两个半径不相等的圆,然后在每一个圆上任意取一段的弧,这个两段弧的度数相等吗?能说这两段弧相等吗?为什么?
辩
辩
一
做一做:
如图2,在圆O中,∠AOB=135°,求的度数
区别弧和弧的度数
例题讲解
教学过程
导
探
练
结
例1 用直尺和圆规把圆四等分。
例2 证明:在同圆或等圆中,相等的圆心角所对的两条弦的弦心距相等。
已知:图3,在圆中,,OE是弦AB的弦心距,OF是弦CD的弦心距。证明:OE=OF。
证明:
(圆心角定理).
(垂径定理)
同理,,所以,
教学过程
导
探
练
结
(五)总结提升,打下伏笔
1、圆心角:顶点在圆心的角。
2、圆是中心对称图形,圆心是它的对称中心。
3、圆具有旋转不变性。
4、圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。所对的弦心距也相等。
5、弧的度数和它所对圆心角的度数相等。
弧
圆心角
弦
弦心距
补充说明
作业布置
板书设计
课内练习1,2题;作业题2,4题。
同课章节目录
