浙教版九年级数学下册 3.3 由三视图描述几何体 课件 (共18张PPT)
文档属性
| 名称 | 浙教版九年级数学下册 3.3 由三视图描述几何体 课件 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
§3.3
如图几何体:
长方体:
长:20cm,
宽:10cm,
高:10cm,
圆柱:
底面半径是5cm,
高是10cm.
用这些信息足够描述出这个几何体模型吗?
2cm
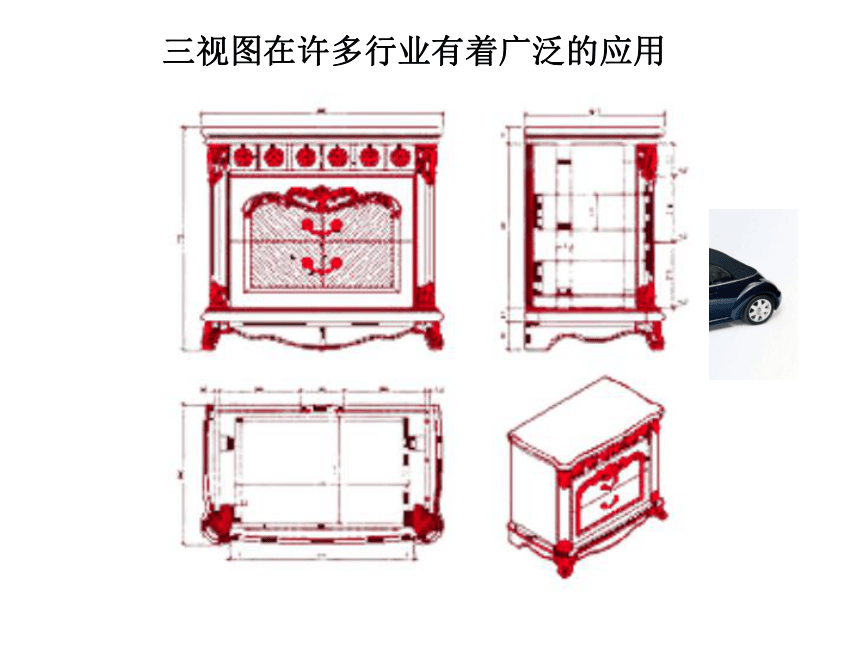
三视图在许多行业有着广泛的应用
由三视图描述几何体(或实物原型)的一般方法是什么?
③ 确定尺寸:
根据三个视图“长对正,高平齐,宽相等”的关
系,确定轮廓线的位置,以及各个方向的尺寸.
① 视图想象:
根据各视图想象从各个方向看到的几何体形状;
② 综合定形:
综合确定几何体(或实物原型)的形状;
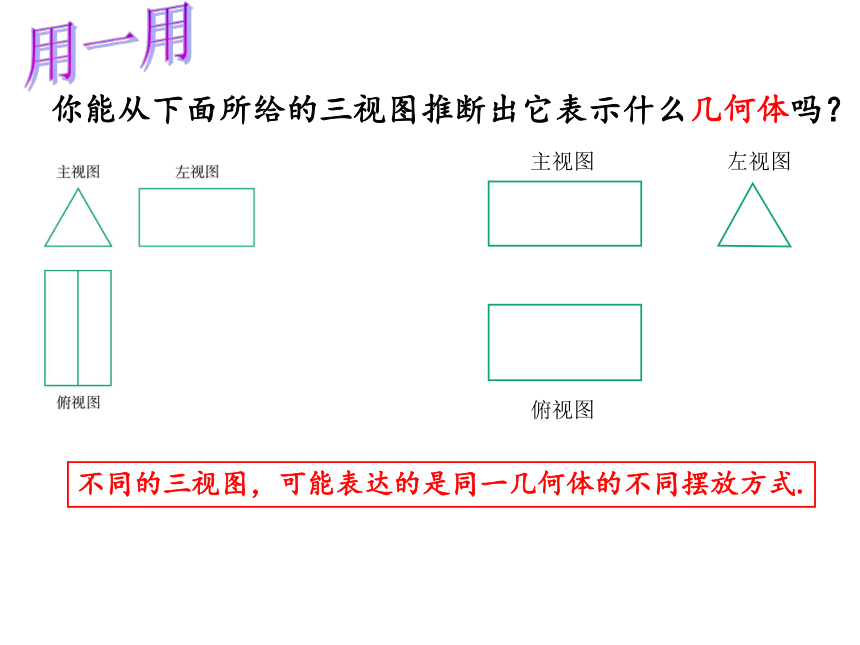
你能从下面所给的三视图推断出它表示什么几何体吗?
不同的三视图,可能表达的是同一几何体的不同摆放方式.
已知一个几何体的三视图如图1所示,
(1)这是什么几何体呢?
图1
6cm
20cm
3cm
4cm
直棱柱的侧面积=底面周长×高
(2)该几何体的形状如图2, 求它的侧面积.
一个几何体的三视图如图所示,这个几何
体的形状是什么?你能求出它的表面积吗?
主视图
俯视图
用小立方块搭几何体,使得它的主视图和俯视图如图所示,这样的几何体需要几块小立方体?
用6个相同的小立方块搭几何体,它的俯视图如图1所示,能搭多少种不同的几何体?
…
(请在俯视图方格中标出在该位置小立方体的个数)
有一个人,收藏了三只古怪的瓶子,它们的
瓶口形状分别如图.现在他想做一只瓶塞,对三个
瓶子都适用,这能做到吗?
请发挥你的想象力,用橡皮泥尝试设计.
你能想象出三个视图分别是两个半径相等的圆和
一个正方形的几何体吗?
牟合方盖就是这样的几何体,它是由两个圆柱分别从
纵横两个方向嵌入一个正方体时两圆柱公共部分形成的.
我国古代数学家利用“牟合方盖” 找到了球体体积的
计算方法。
根据三视图描述简单的几何体,你有哪些方法或经验?
1.作业本§3.3
2.课外思考题:
尝试设计一个几何体的三个视图分别是圆、等腰三角形和一个长方形.
§3.3
如图几何体:
长方体:
长:20cm,
宽:10cm,
高:10cm,
圆柱:
底面半径是5cm,
高是10cm.
用这些信息足够描述出这个几何体模型吗?
2cm
三视图在许多行业有着广泛的应用
由三视图描述几何体(或实物原型)的一般方法是什么?
③ 确定尺寸:
根据三个视图“长对正,高平齐,宽相等”的关
系,确定轮廓线的位置,以及各个方向的尺寸.
① 视图想象:
根据各视图想象从各个方向看到的几何体形状;
② 综合定形:
综合确定几何体(或实物原型)的形状;
你能从下面所给的三视图推断出它表示什么几何体吗?
不同的三视图,可能表达的是同一几何体的不同摆放方式.
已知一个几何体的三视图如图1所示,
(1)这是什么几何体呢?
图1
6cm
20cm
3cm
4cm
直棱柱的侧面积=底面周长×高
(2)该几何体的形状如图2, 求它的侧面积.
一个几何体的三视图如图所示,这个几何
体的形状是什么?你能求出它的表面积吗?
主视图
俯视图
用小立方块搭几何体,使得它的主视图和俯视图如图所示,这样的几何体需要几块小立方体?
用6个相同的小立方块搭几何体,它的俯视图如图1所示,能搭多少种不同的几何体?
…
(请在俯视图方格中标出在该位置小立方体的个数)
有一个人,收藏了三只古怪的瓶子,它们的
瓶口形状分别如图.现在他想做一只瓶塞,对三个
瓶子都适用,这能做到吗?
请发挥你的想象力,用橡皮泥尝试设计.
你能想象出三个视图分别是两个半径相等的圆和
一个正方形的几何体吗?
牟合方盖就是这样的几何体,它是由两个圆柱分别从
纵横两个方向嵌入一个正方体时两圆柱公共部分形成的.
我国古代数学家利用“牟合方盖” 找到了球体体积的
计算方法。
根据三视图描述简单的几何体,你有哪些方法或经验?
1.作业本§3.3
2.课外思考题:
尝试设计一个几何体的三个视图分别是圆、等腰三角形和一个长方形.
