5.3.2 正方形(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 5.3.2 正方形(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 664.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 12:02:58 | ||
图片预览



文档简介
21世纪教育网 –全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第5章特殊平行四边形
5.3 正 方 形
第2课时 正 方 形(2)
【知识清单】
正方形的性质:
1.正方形的四个角都是直角,四条边相等;
2.正方形的对角线相等,并且互相垂直平分,每条对角线平分一组对角.
【经典例题】
例题1、如图,正方形ABCD中,∠DAF=22.5°,AF交对角线BD于点E,那么∠AEB等于( )
A.35° B.45° C.60° D.70°
【考点】正方形的性质.
【分析】根据已知条件证明△AED≌△CED,即可证明∠ECF=∠DAF=22.5°,从而求得∠BAF=∠BCE=67.5°,再根据四边形的内角和定理即可求解.
【解答】∵四边形ABCD是正方形,BD是对角线,
∴AD=CD,∠ADE=∠CDE,∠DAB=∠ABC=90°,
在△ADE和△CDE中,
∵,
∴△ADE≌△CDE.
∴∠DCE=∠DAF=22.5°,
∵∠DAB=∠ABC=90°,
∴∠BAF=∠BCE=67.5°,
在四边形ABCE中,∠AEC=360°67.5°90°67.5°=135°,
∴∠CEF=180°135°=45°(方法不唯一).
故选B.
【点评】本题主要考查了正方形的性质,正确理解,证明△AED≌△CED是解题的关键.
例题2、如图,正方形ABCD的∠D,∠B分别沿直线EF、MN折叠,点D、点B分别落在点D′、点B′处,∠1+∠2+∠3+∠4=______.
【考点】正方形的性质.
【分析】根据多边形内角和为(n2)×180°,
再根据正方形性质即可得出答案.
【解答】∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=∠D′=∠B′=90°
∵六边形AMNCEF的内角和是:(62)×180°=720°,
∴∠A+∠AFE+∠FEC+∠C+∠CNM+∠NMA=720°.
∴∠AFE+∠FEC+∠CNM+∠NMA=720°∠A∠C
=720°90°90°=540°.
∵∠AFE=∠1+∠D′FE ,∠FEC=∠2 +∠D′EF,
∠CNM=∠3+∠CNB′,∠NMA=∠4+∠NMB′,
∠D′FE+∠D′EF=90°,∠CNB′+∠NMB′=90°,
∴∠1+∠2+∠3+∠4=540°90°90°=360°.
故答案是:360°.
【点评】本题主要考查了多边形内角和公式、直角三角形中两个锐角互余性质及正方形性质,理解轴对称和多边形内角和公式是解决问题的关键.
【夯实基础】
1、正方形具有而菱形不一定具有的特征是( )
A.四边都相等 B.每条对角线平分一组对角
C.对角线相等 D.对角线互相垂直平分
2、下列图形中:①正方形;②线段;③三角形;④一个角;⑤平行四边形;⑥圆;⑦等腰梯形. 既
是中心对称图形,又是轴对称图形的个数是( )
A.3个 B.4个 C.5个 D.6个
3、如图,已知点P为正方形ABCD内一点,且PA=PB=10cm,点P到边AD的距离也为10cm,
则正方形ABCD的对角线边长为( )cm.
A.8 B.8 C.16 D.16
4、如图,边长为1的正方形ABCD绕着点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的
面积为( )
A. B. C.1 D.2
5、图中的矩形是由六个正方形组成,其中正方形①的面积为1,④和⑥的边长相等,则正方形
③的面积为 .
6、如图,在正方形ABCD的外侧,作等边三角形DEC,连结AE、BE,则∠AEB的度数为 .
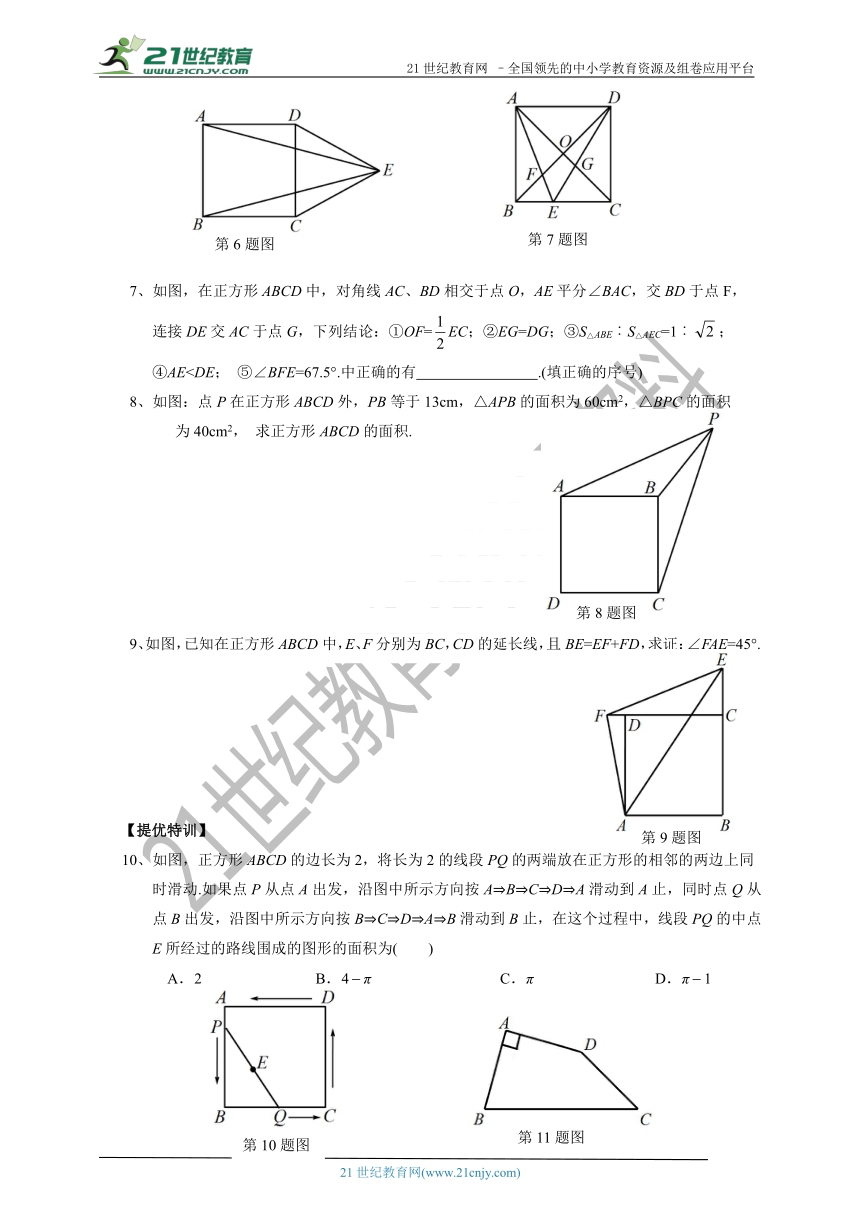
7、如图,在正方形ABCD中,对角线AC、BD相交于点O,AE平分∠BAC,交BD于点F,
连接DE交AC于点G,下列结论:①OF=EC;②EG=DG;③S△ABE︰S△AEC=1︰;
④AE
为40cm2, 求正方形ABCD的面积.
9、如图,已知在正方形ABCD中,E、F分别为BC,CD的延长线,且BE=EF+FD,求证:∠FAE=45°.
【提优特训】
10、如图,正方形ABCD的边长为2,将长为2的线段PQ的两端放在正方形的相邻的两边上同
时滑动.如果点P从点A出发,沿图中所示方向按A?B?C?D?A滑动到A止,同时点Q从点B出发,沿图中所示方向按B?C?D?A?B滑动到B止,在这个过程中,线段PQ的中点E所经过的路线围成的图形的面积为( )
A.2 B.4π C.π D.π1
11、如图,在四边形ABCD中,AB=AD=DC,∠BAD=90°,∠ADC=150°,则∠ABC的度数为( )
A.50°?? B.55°? C.65°? D.75°
12、如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角
线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. ? ? B.2? C. ? D.2
13、如图,四边形ABCD是正方形,点E是BA延长线上一点,以DE为边长作正方形DEFG,
若正方形ABCD和正方形DGFE的面积分别是7cm2和11cm2,则△CDG的面积为( ) cm2
A.2 ?? B.4? C.? D.
14、如图,正方形ABCD的边长为6,点E在AB边上.四边形EFQB也为正方形,设△AFC的
面积为S,则S=????? ?????.?
15、已知正方形ABCD边长为10cm,P是AB上任意一点,则点P到对角线AC、BD的距离之
和等于 ?cm.
16、如图,正方形ABCD的面积为5cm2,E,F分别为CD,DA的中点,BE,CF交于点P.求
AP的长.
17、如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三
角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.
(1)由几个不同的位置,分别测量AE、EF、FC的长,从中你能发现AE、EF、FC的数量之
间具有怎样的关系?并证明你所得到的结论;
(2)设AE=x,CF=y,求y与x之间的函数解析式,
并写出函数的定义域.
18、如图,△ABC中,点O是AC上一动点,过点O作直线MN∥BC,设MN交∠ACB的平分线
于点E,交∠ACG的平分线于点F.
(1)求证:OE=OF;
(2)若CE=,CF=,求OC的长;
(3)当点O运动到何处时,四边形AECF是矩形;
(4)当O是AC上怎样的点,且AC与BC具有
什么关系时,四边形AECF是正方形?
【中考链接】
19、(2019?四川巴中)下列命题是真命题的是(??)?
A.对角线相等的四边形是矩形?? B.对角线互相垂直的四边形是矩形?
? C.对角线互相垂直的矩形是正方形?? D.四边相等的平行四边形是正方形
20、 (2019?浙江丽水) 将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,
展开铺平后得到图⑤,其中FM,GN是折痕.若正方形EFGH与五边形MCNGF的面积相
等,则的值是( )
A.?????????B.﹣1???????????C.??????????????D.
21、(2019?甘肃兰州) 如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形
ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则DM=(?????)
A.?????????B.?????????C.?-1????? D.?-1
参考答案
1、C 2、B 3、D 4、C 5、36 6、30° 7、①③④⑤ 10、B 11、D 12、B
13、D 14、18 15、 19、C 20、A 21、D
8、如图:点P在正方形ABCD外,PB等于13cm,△APB的面积为60cm2,△BPC的面积
为40cm2, 求正方形ABCD的面积.
解:∵△APB的面积为40,△BPC的面积为20,
∴P到AB的距离:P到BC的距离等于3:2,
设P到BC的距离PE为2x,则P到AB的距离EB为3x,
在Rt△BPE中,(2x)2+(3x)2=132,
∴x2=13,
∵x >0,
解得:x=,2 x=2,
∴?BC?2=40
解得:BC= x=,
故BC2=,即正方形ABCD的面积为cm2.
9、如图,已知在正方形ABCD中,E、F分别为BC,CD的延长线,且BE=EF+FD,求证:∠FAE=45°.
证明:在BE上截取BG=DF,连结AG,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=∠ADC=∠DCB=∠CBA=90°,
在△ABG和△ADF中
∵
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF.
∵∠BAG+∠GAD=90°,
∴∠GAD+∠DAF=90°,即∠GAF=90°.
∵BE=EF+FD,BG=DF,
∴BG+GE= EF+FD,
∴EG=EF.
在△AFE和△AGE中
∵
∴△AFE≌△AGE(SSS),
∴∠FAE=∠GAE=∠GAF=45°.
16、如图,正方形ABCD的面积为5cm2,E,F分别为CD,DA的中点,BE,CF交于点P.求
AP的长.
解:延长CF、BA交于点M,如图所示
∵四边形ABCD是正方形,正方形ABCD的面积为5cm2,
∴AB=BC=CD=DA=cm,∠BAD=∠BCE=∠D=90°,
∴∠MAF=90°,
∵E,F分别为CD,AD的中点,
∴CE=DE=DF=AF,
在△BCE和△CDF中,
∵,
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF.
∵∠DCF+∠BCP=90°,
∴∠CBE+∠BCP=90°,
∴∠BPM=∠CBE+∠BCP=90°.
在△CDF和△MAF中,
∵,
∴△CDF≌△MAF(ASA),
∴CD=AM.
∵CD=AB,
∴AB=AM.
∴PA是Rt△BPM斜边BM上的中线,
∴AP=BM,
∴AP=AB=cm.
17、如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三
角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.
(1)由几个不同的位置,分别测量AE、EF、FC的长,从中你能发现AE、EF、FC的数量之
间具有怎样的关系?并证明你所得到的结论;
(2)设AE=x,CF=y,求y与x之间的函数解析式,并写出函数的定义域.
解:(1)EF=AE+FC.
理由:如图所示:延长BC至M,使CM=AE,连接DM,
在△DAE和△DCM中,
∵,
∴△DAE≌△DCM(SAS),
∴DE=DM,∠ADE=∠CDM,
∠FDM=∠FDC+∠CDM=∠FDC+∠ADE=90°-∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF=CM+FC=AE+FC;
(2)如图所示,已知AE=x,CF=y,则BE=6x,BF=6y,
由(1)可知EF=x+y,
在Rt△BEF中,由勾股定理,得
BE2+BF2=EF2,即(6x)2+(6y)2=(x+y)2,
解得:y=(0≤x≤6).
18、如图,△ABC中,点O是AC上一动点,过点O作直线MN∥BC,设MN交∠ACB的平分线
于点E,交∠ACG的平分线于点F.
(1)求证:OE=OF;
(2)若CE=,CF=,求OC的长;
(3)当点O运动到何处时,四边形AECF是矩形;
(4)当O是AC上怎样的点,且AC与BC具有
什么关系时,四边形AECF是正方形?
(1)证明:∵MN交∠ACB的平分线于点E,
交∠ACB的外角平分线于点F,
∴∠1=∠2,∠3=∠4,
∵MN∥BC,
∴∠2=∠5,∠4=∠6,
∴∠1=∠5,∠3=∠6,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4=90°,
∵CE=,CF=
∴EF==3,
∴OC=EF=1.5;
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
(4)由(3)可知四边形AECF是矩形,要使AECF为正方形,必须使EF⊥AC,
∵EF∥BC,
∴BC⊥AC,
∴△ABC是以∠ACB为直角的直角三角形,?
∴当点O为AC中点且△ABC是以∠ACB为直角的直角三角形时,四边形AECF是正方形.
第9题图
第21题图
第20题图
第16题图
第18题图
第17题图
第18题图
第8题图
第17题图
第16题图
第18题图
第7题图
例题2图
第9题图
第17题图
第16题图
第6题图
第8题图
第5题图
第4题图
第9题图
第14题图
第13题图
第12题图
第11题图
第10题图
例题1图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
