第5章 特殊平行四边形单元检测题1(含答案)
文档属性
| 名称 | 第5章 特殊平行四边形单元检测题1(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 674.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 20:52:38 | ||
图片预览


文档简介
21世纪教育网 –全国领先的中小学教育资源及组卷应用平台
浙教版2019-2020学年度下学期八年级数学(下册)
第5章特殊平行四边形检测题1(有答案)
(时间:100分钟 满分:120分)
题号 1 2 3 4 5 6 7 8 9 10
答案
一、选择题(共10小题 每3分 共30分)
1.菱形、矩形、正方形都具有的性质是( )
A. 对角线相等且互相平分 B. 对角线相等且互相垂直平分
C. 对角线互相平分 D. 对角线平分一组对角
2.如图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,则∠EAF等于( )
A.75° B.60° C.45° D.30°
3.在直角坐标系中,点A(2,0),B(2,1),C(1,3),若四边形ABCD为菱形,则点D的坐标为( )
A.(3,4) B.(5,2) C.(3,4) D.(5,2)
4.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF//BC,分别交AB,CD于
E、F,连接PB.若△PEB 的面积为S1,△APF的面积为S2,则S1与S2的大小关系为( )
A.S1>S2 B.S1
动,那么△BCP的面积S与点P运动的路程x之间的函数图象大致是(?? ??)
6.如图,正方形ABCD中,∠DAF=22.5°,AF交对角线BD于点E,那么∠AEB等于( )
A.35° B.45° C.60° D.70°
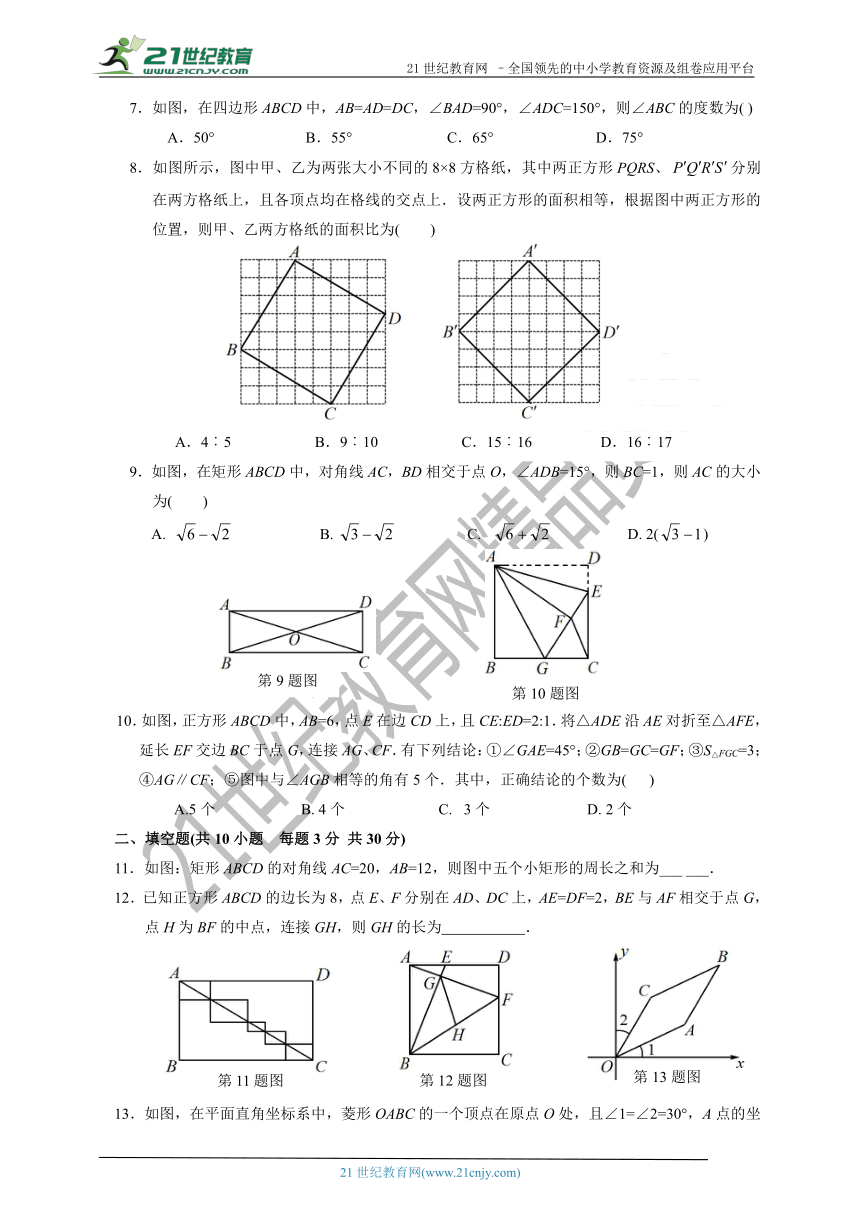
7.如图,在四边形ABCD中,AB=AD=DC,∠BAD=90°,∠ADC=150°,则∠ABC的度数为( )
A.50°?? B.55°? C.65°? D.75°
8.如图所示,图中甲、乙为两张大小不同的8×8方格纸,其中两正方形PQRS、分别在两方格纸上,且各顶点均在格线的交点上.设两正方形的面积相等,根据图中两正方形的位置,则甲、乙两方格纸的面积比为( )
A.4︰5 B.9︰10 C.15︰16 D.16︰17
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ADB=15°,则BC=1,则AC的大小
为(?? )
A. ???????????? ????B.???????????????????C.? ?????????????? ???D.?2()
10.如图,正方形ABCD中,AB=6,点E在边CD上,且CE:ED=2:1.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.有下列结论:①∠GAE=45°;②GB=GC=GF;③S△FGC=3;④AG∥CF;⑤图中与∠AGB相等的角有5个.其中,正确结论的个数为( )
A.5个???????????? ????B.?4个??????????? ???????C.? 3个???????????? ?? ???D.?2个
二、填空题(共10小题 每题3分 共30分)
11.如图:矩形ABCD的对角线AC=20,AB=12,则图中五个小矩形的周长之和为___ ___.
12.已知正方形ABCD的边长为8,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
13.如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠1=∠2=30°,A点的坐
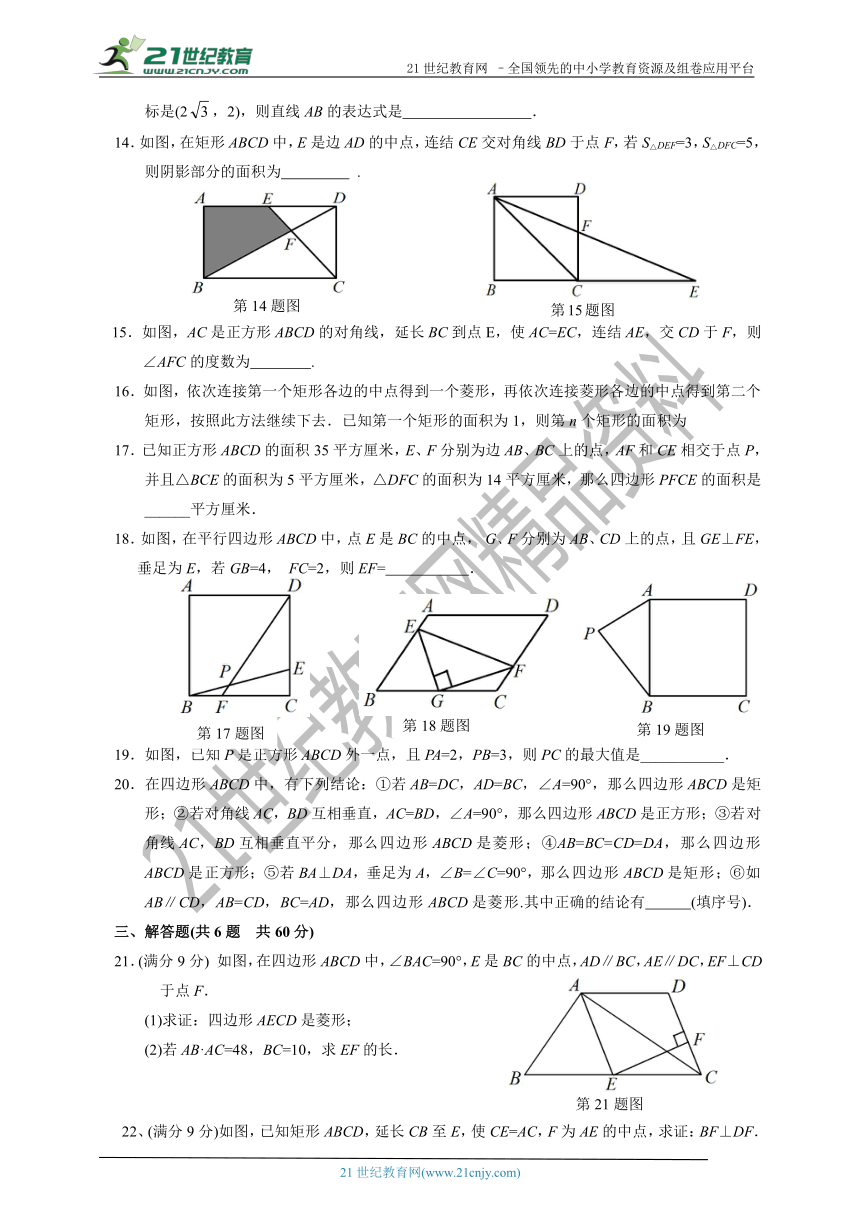
标是(2,2),则直线AB的表达式是 .
14.如图,在矩形ABCD中,E是边AD的中点,连结CE交对角线BD于点F,若S△DEF=3,S△DFC=5,
则阴影部分的面积为 .
15.如图,AC是正方形ABCD的对角线,延长BC到点E,使AC=EC,连结AE,交CD于F,则∠AFC的度数为 .
16.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为
17.已知正方形ABCD的面积35平方厘米,E、F分别为边AB、BC上的点,AF和CE相交于点P,并且△BCE的面积为5平方厘米,△DFC的面积为14平方厘米,那么四边形PFCE的面积是______平方厘米.
18.如图,在平行四边形ABCD中,点E是BC的中点, G、F分别为AB、CD上的点,且GE⊥FE,垂足为E,若GB=4, FC=2,则EF= .
19.如图,已知P是正方形ABCD外一点,且PA=2,PB=3,则PC的最大值是___________.
20.在四边形ABCD中,有下列结论:①若AB=DC,AD=BC,∠A=90°,那么四边形ABCD是矩形;②若对角线AC,BD互相垂直,AC=BD,∠A=90°,那么四边形ABCD是正方形;③若对角线AC,BD互相垂直平分,那么四边形ABCD是菱形;④AB=BC=CD=DA,那么四边形ABCD是正方形;⑤若BA⊥DA,垂足为A,∠B=∠C=90°,那么四边形ABCD是矩形;⑥如AB∥CD,AB=CD,BC=AD,那么四边形ABCD是菱形.其中正确的结论有 (填序号).
三、解答题(共6题 共60分)
21.(满分9分) 如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB·AC=48,BC=10,求EF的长.
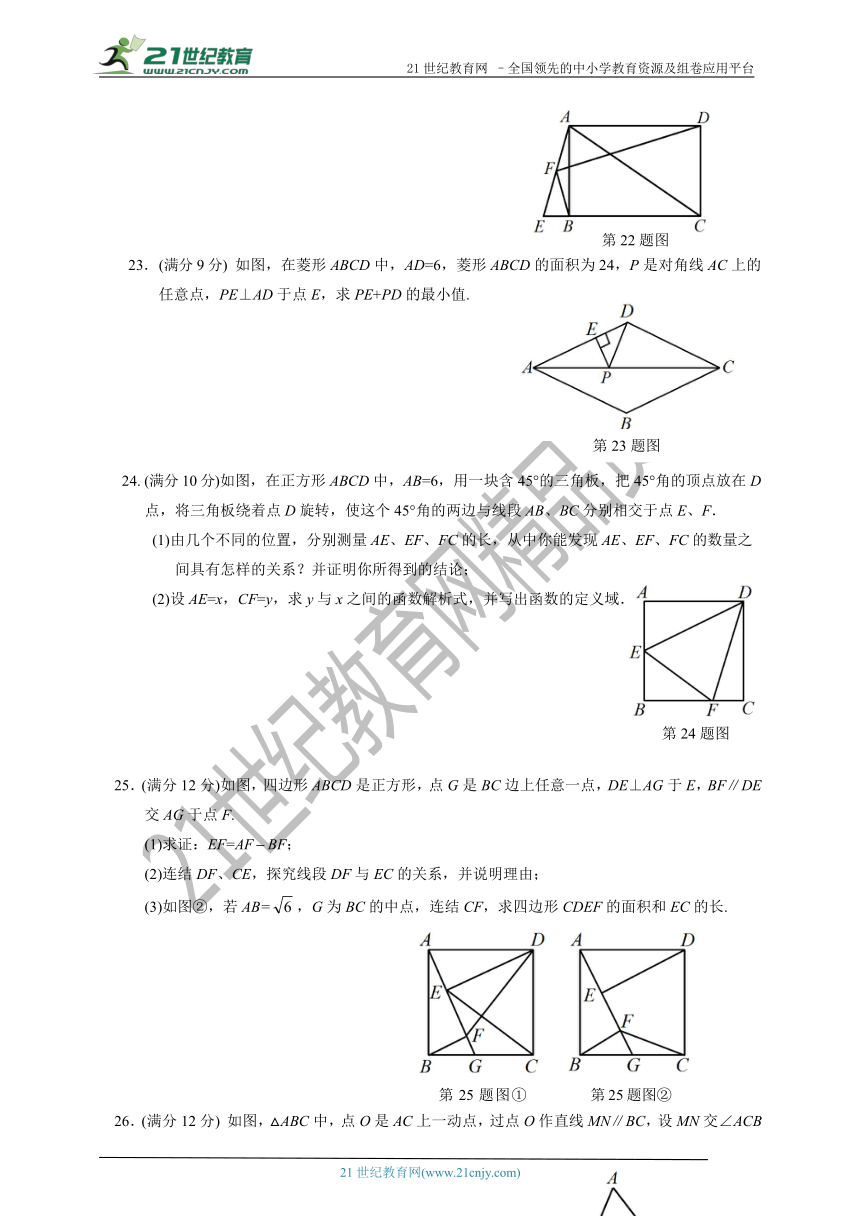
22、(满分9分)如图,已知矩形ABCD,延长CB至E,使CE=AC,F为AE的中点,求证:BF⊥DF.
23.(满分9分) 如图,在菱形ABCD中,AD=6,菱形ABCD的面积为24,P是对角线AC上的任意点,PE⊥AD于点E,求PE+PD的最小值. .
24. (满分10分)如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.
(1)由几个不同的位置,分别测量AE、EF、FC的长,从中你能发现AE、EF、FC的数量之
间具有怎样的关系?并证明你所得到的结论;
(2)设AE=x,CF=y,求y与x之间的函数解析式,并写出函数的定义域.
25.(满分12分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE交AG于点F.
(1)求证:EF=AFBF;
(2)连结DF、CE,探究线段DF与EC的关系,并说明理由;
(3)如图②,若AB=,G为BC的中点,连结CF,求四边形CDEF的面积和EC的长.
26.(满分12分) 如图,△ABC中,点O是AC上一动点,过点O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACG的平分线于点F.
(1)求证:OE=OF;
(2)若CE=,CF=,求OC的长;
(3)当点O运动到何处时,四边形AECF是矩形;
(4)当点O在边AC上运动时,四边形BCFE会是菱形吗?
若是,请证明;若不是,则说明理由;
(5)当O是AC上怎样的点,且AC与BC具有
什么关系时,四边形AECF是正方形?
参考答案
一、选择题(共10小题 每3分 共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C B B D D A C
二、填空题(共10小题 每题3分 共30分)
11、56 12、5 13、y= 14、11 15、112.5° 16、
17、 18、6 19、2+3 20、①、③、⑤.
三、解答题(共6题 共60分)
21.(满分9分) 如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB·AC=48,BC=10,求EF的长.
21、证明:(1)∵AD∥BC,AE∥DC,?
∴四边形AECD是平行四边形,?
∵∠BAC=90°,E是BC的中点,
? ∴AE=CE=BC,?
∴四边形AECD是菱形;
(2)∵AB·AC=48,BC=10,?
∴AE=BC=5.
∴△ABC的面积=AB·AC=24.
∵E是BC的中点,,
∴△ABE的面积=△AEC的面积.?
∵四边形AECD是菱形,
∴△ADC的面积=△AEC的面积.
∴△ABC的面积=菱形AECD的面积,
?∴AE·EF=24.
?∴EF=.
22、(满分9分)如图,已知矩形ABCD,延长CB至E,使CE=AC,F为AE的中点,求证:BF⊥DF.
证明:连接CF,
∵CE=CA,F为AE的中点,
∴∠1+∠2=90°.
∵四边形ABCD是矩形,
∴∠ABC=∠ABE=∠BAD=90°,BC=AD,
∵F为AE的中点,
∴BF=AF=EF,∠FBA=∠FAB,
∴∠ABC+∠FBA =∠BAD+∠FAB,
即∠FBC=∠FAD.
在△FBC和△FAD中,
∵,
∴△FBC≌△FAD(SAS).
∴∠1=∠3,∠2+∠3=90°.
∴BF⊥DF.
23.(满分9分) 如图,在菱形ABCD中,AD=6,菱形ABCD的面积为24,P是对角线AC上的任意点,PE⊥AD于点E,则PE+PD的最小值为 .
解:过点B作EB⊥AD交AD于E,连接PD,
∵四边形ABCD是菱形,
∴线段AC、BD互相垂直平分,
∴B、D关于AC对称,则PD=PB,
∴PE+PD=PE+BP=BE,
即BE就是PE+PD的最小值.
∵AD=6,菱形ABCD的面积为24,
∴AD·BE=24,
∵BE=4,
∴PE+PD的最小值4.
24. (满分10分)如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.
(1)由几个不同的位置,分别测量AE、EF、FC的长,从中你能发现AE、EF、FC的数量之
间具有怎样的关系?并证明你所得到的结论;
(2)设AE=x,CF=y,求y与x之间的函数解析式,并写出函数的定义域.
解:(1)EF=AE+FC.
理由:如图所示:延长BC至M,使CM=AE,连接DM,
在△DAE和△DCM中,
∵,
∴△DAE≌△DCM(SAS),
∴DE=DM,∠ADE=∠CDM,
∴∠FDM=∠FDC+∠CDM=∠FDC+∠ADE=90°-∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF=CM+FC=AE+FC;
(2)如图所示,已知AE=x,CF=y,则BE=6x,BF=6y,
由(1)可知EF=x+y,
在Rt△BEF中,由勾股定理,得
BE2+BF2=EF2,即(6x)2+(6y)2=(x+y)2,
解得:y=(0≤x≤6).
25.(满分12分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE交AG于点F.
(1)求证:EF=AFBF;
(2)连结DF、CE,探究线段DF与EC的关系,并说明理由;
(3)如图②,若AB=,G为BC的中点,连结CF,求四边形CDEF的面积和EC的长.
证明:(1)如图③:∵ABCD是正方形,
∴AD=AB,∠BAD=∠ADC =90°
∵DE⊥AG,
∴∠AED=90°
∴∠1+∠3=90°
又∵∠2+∠3=∠BAD=90°,
∴∠1=∠2.
∵BF∥DE,
∴∠AFB=∠DEG=∠AED.
在△DAE与△ABF中,
∵,
∴△DAE≌△ABF(AAS).
∴AE = BF.
∵AF=AE+EF,
∴EF=AFBF.
(2)如图③:EC=DF,且EC⊥DF,
由(1)知△DAE≌△ABF
∴DE=AF,
∵∠1+∠3=90°,∠1+∠EDC=90°,
∴∠3=∠EDC.
在△AFD与△DEC中,
∵,
∴△AFD≌△DEC(AAS).
∴DF=EC,∠ADF=∠DCE,
∵∠ADF+∠FDC=90°,
∴∠DCE +∠FDC=90°,
∴EC⊥DF.
(3) 如图④:∵ AB=,G为BC的中点,
∴BG===, S△BGF= S△CBG.
∵△ABF≌△DAE,
∴S△ABF= S△DAE.
∴四边形CDEF的面积=S正方形ABCD - S△ABF - S△DAE - S△BGF - S△CBG
=S正方形ABCD2S△ABF2 S△BGF
=S正方形ABCD2( S△ABF+ S△BGF)
=S正方形ABCD2S△ABG
=2×AB·BG=×=3.
由(2) EC=DF,且EC⊥DF,
∴S四边形CDEF=EC·DF=3
EC2=DF2=6,解得CE=DF=.
26.(满分12分) 如图,△ABC中,点O是AC上一动点,过点O作直线MN∥BC,设MN交∠ACB的平分线
于点E,交∠ACG的平分线于点F.
(1)求证:OE=OF;
(2)若CE=,CF=,求OC的长;
(3)当点O运动到何处时,四边形AECF是矩形;
(4)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,
请证明;若不是,则说明理由;
(5)当O是AC上怎样的点,且AC与BC具有
什么关系时,四边形AECF是正方形?
(1)证明:∵MN交∠ACB的平分线于点E,
交∠ACB的外角平分线于点F,
∴∠1=∠2,∠3=∠4,
∵MN∥BC,
∴∠2=∠5,∠4=∠6,
∴∠1=∠5,∠3=∠6,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4=90°,
∵CE=,CF=
∴EF==3,
∴OC=EF=1.5;
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
(4) 当点O在边AC上运动时,四边形BCFE不会是菱形,
理由:∵△ECF是直角三角形,EF为斜边,
∴EF>CF,
∴四边形BCFE不会是菱形.
(5)由(3)可知四边形AECF是矩形,要使AECF为正方形,必须使EF⊥AC,
∵EF∥BC,
∴BC⊥AC,
∴△ABC是以∠ACB为直角的直角三角形,?
∴当点O为AC中点且△ABC是以∠ACB为直角的直角三角形时,四边形AECF是正方形.
第25题图②
第25题图③①
第24题图
第13题图
第24题图
第19题图
第17题图
第4题图
第23题图
第23题图
第25题图①①
第12题图
第25题图①①
第26题图
第23题图
第25题图④
第10题图
第2题图
第24题图
第22题图
第26题图
第22题图
第6题图
第21题图
第9题图
第25题图②
第22题图
第21题图
第14题图
第7题图
第11题图
第15题图
第18题图
A B C D
第26题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
