第5章 特殊平行四边形单元检测题2(含答案)
文档属性
| 名称 | 第5章 特殊平行四边形单元检测题2(含答案) | 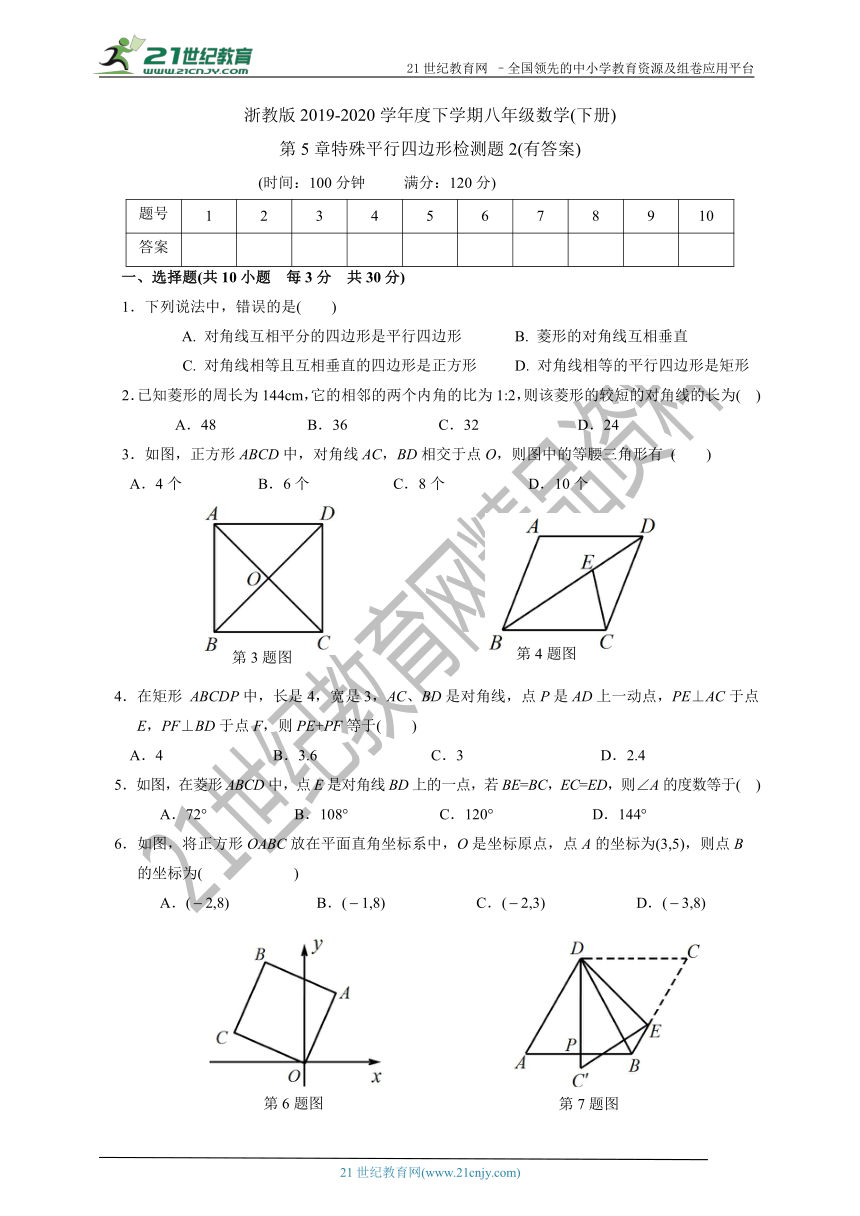 | |
| 格式 | zip | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 16:25:33 | ||
图片预览




文档简介
21世纪教育网 –全国领先的中小学教育资源及组卷应用平台
浙教版2019-2020学年度下学期八年级数学(下册)
第5章特殊平行四边形检测题2(有答案)
(时间:100分钟 满分:120分)
题号 1 2 3 4 5 6 7 8 9 10
答案
一、选择题(共10小题 每3分 共30分)
1.下列说法中,错误的是( )
A. 对角线互相平分的四边形是平行四边形 B. 菱形的对角线互相垂直
C. 对角线相等且互相垂直的四边形是正方形 D. 对角线相等的平行四边形是矩形
2.已知菱形的周长为144cm,它的相邻的两个内角的比为1:2,则该菱形的较短的对角线的长为( )
A.48 B.36 C.32 D.24
3.如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有 ( )
A.4个 B.6个 C.8个 D.10个
4.在矩形 ABCDP中,长是4,宽是3,AC、BD是对角线,点P是AD上一动点,PE⊥AC于点
E,PF⊥BD于点F,则PE+PF等于( )
A.4? B.3.6 C.3 D.2.4
5.如图,在菱形ABCD中,点E是对角线BD上的一点,若BE=BC,EC=ED,则∠A的度数等于( )
A.72°? B.108° C.120° D.144°
6.如图,将正方形OABC放在平面直角坐标系中,O是坐标原点,点A的坐标为(3,5),则点B
的坐标为( )
A.(2,8)? B.(1,8) C.(2,3) D.(3,8)
7.如图,菱形纸片ABCD中,∠A=60°,菱形纸片ABCD沿着直线DE折叠(点E在边BC上),
使点C落在DP(P为AB中点)所在的直线上.则∠DEC的大小为( ).
A.50°?? B.55°? C.65°? D.75°
8.如图,已知点P为正方形ABCD内一点,且PA=PB=10cm,点P到边AD的距离也为10cm,
则正方形ABCD的对角线边长为( )cm.
A.16 B.16 C.8 D.8
9.已知,如图,过正方形ABCD的顶点C作对角线BD的平行线,在这条线上取一点E,使BE=BD连结DE,则∠CED的度数为( )
A.75° B.90° C.105° D.125°
10.如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交
于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:①△BDF≌△DCE;
②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD=AM2.其中正确结论的个数是( ?)
A.3? ? B.2?? ? C.1??? D.0
二、填空题(共10小题 每题3分 共30分)
11.将一正方形按如图方式分成n个全等矩形,上、下各横排两个,中间竖排若干个,则n的值为 .
12.如图,矩形ABCD中,AB=3,BC=4,点E为AD上的一动点,将△BAE沿BE向矩形的内部
折叠,若点A的对应点为 恰好落在∠BCD的平分线上时,则= .
13.如图,正方形DEFG内接于等边三角形ABC中,点D、E在BC边上,G、F分别在边AB和AC上,若等边三角形ABC的边长为(2+)cm,则正方形DEFG的面积为 .
14.如图,平面直角坐标系中,矩形OABC的顶点A(6,0),C(0,2).将矩形OABC绕点O
顺时针方向旋转,使点A恰好落在OB上的点A1处,若点B的对应点B1, 点C的对应点C1,
则直线B1C1的解析式为 .
15.如图,已知菱形ABCD的周长为12cm, AC=AB,点F、E分别在AB、BC上,过点F
作FG⊥DC于点G,连接FE,若∠EFG=15°,AF=1cm,则BE的等于 .
16.已知:如图,正方形ABCD的边长为8 cm,E在DC上,且DE=2 cm,P是AC上的一动点,则PD+PE的最小值为 .
17.已知一直角三角形的两边长恰为方程(2x+1)(x3)=(x+7)(x5)+20的两个根,则此直角三角形
斜边上的中线长是 .
18.如图,在矩形ABCD中,对角线长5,且∠1=∠2=∠3=∠4,则四边形EFGH的周长为 10 .
19.四边形ABCD的四条边分别为a、b、c、d,满足(a+b+c)2=3a2+3b2+3c2,3d=a+b+c,则四边
形形状为 ? .
20.如图,将△ADH绕点H顺时针旋转90°,点M、E的对应点分别为D、A,连结DM,△BCE
是△ADM沿 MA的方向平移到的,连结CD,CH,则有以下结论:①四边形ABCD是正方
形;②C、H、A三点,在一条直线上;③CE=DH;④若∠CHD=60°时,DM=2AM. .
三、解答题(共6题 共60分)
21.(满分9分) 如图,点E是矩形ABCD边上一点,AE=AD,AD>AB,过点D作DF⊥AE,垂足为点F,探究DF与AB的有和数量关系,并证明你的结论.
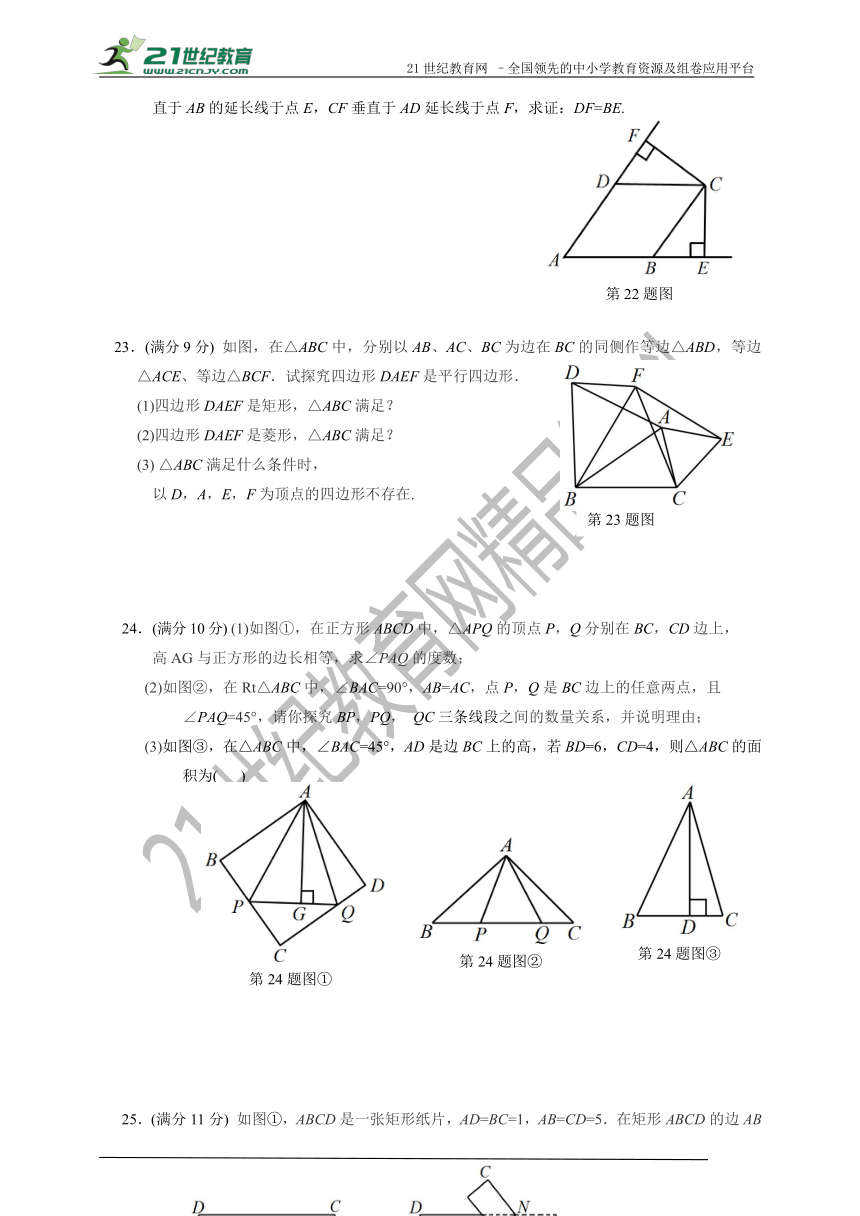
22.(满分9分)如图,已知四边形ABCD是菱形,点E、F分别是AB、AD延长线上的点,CE垂
直于AB的延长线于点E,CF垂直于AD延长线于点F,求证:DF=BE.
23.(满分9分) 如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.试探究四边形DAEF是平行四边形.
(1)四边形DAEF是矩形,△ABC满足?
(2)四边形DAEF是菱形,△ABC满足?
(3) △ABC满足什么条件时,
以D,A,E,F为顶点的四边形不存在.
24.(满分10分) (1)如图①,在正方形ABCD中,△APQ的顶点P,Q分别在BC,CD边上,
高AG与正方形的边长相等,求∠PAQ的度数;
(2)如图②,在Rt△ABC中,∠BAC=90°,AB=AC,点P,Q是BC边上的任意两点,且
∠PAQ=45°,请你探究BP,PQ, QC三条线段之间的数量关系,并说明理由;
(3)如图③,在△ABC中,∠BAC=45°,AD是边BC上的高,若BD=6,CD=4,则△ABC的面积为( )
25.(满分11分) 如图①,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)如图②,若∠1=70°,求∠MKN的度数;
(2)如图③,△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值.
26.(满分12分) 如图,在Rt△ABC中,∠B=90°,AC=72 cm,∠A=60°,点P从点C出发沿CA方向以6 cm/秒的速度向点A匀速运动,同时点Q从点A出发沿AB方向以3cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P,Q运动的时间是t秒(0<t≤12).过点P作PD⊥BC于点D,连结PQ,DQ.
(1)求证:AQ=PD;
(2)四边形APDQ能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)四边形PDBQ能够成为矩形吗?如果能,求出相应的t值,如果不能,说明理由.
(4)四边形PDBQ能够成为正方形吗?如果能,求出相应的t值,如果不能,说明理由.
参考答案
一、选择题(共10小题 每3分 共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D B A D A C A
二、填空题(共10小题 每题3分 共30分)
11、8 12、 13、3cm2 14、y= 15、 16、10cm
17、2.5或2 18、10 19、菱形或正方形 20、①②③④
三、解答题(共6题 共60分)
21.(满分9分) 如图,点E是矩形ABCD边上一点,AE=AD,AD>AB,过点D作DF⊥AE,垂足为点F,探究DF与AB的有和数量关系,并证明你的结论.
证明:DF=AB
∵四边形ABCD是矩形
∴AD//BC,∠C=90°,AB=CD?,
∴∠DAF=∠CED?,
∵AD=AE,
∴∠AED=∠DEC,
∴∠FED=∠CED.
∵DF⊥AE,
∴∠DFE=∠C=90°.
在△FDE和△CED中
∵
∴△FDE≌△CED
∴DF=CD
∴DF=AB.
22.(满分9分)如图,已知四边形ABCD是菱形,点E、F分别是AB、AD延长线上的点,CE垂
直于AB的延长线于点E,CF垂直于AD延长线于点F,求证:DF=BE.
证明:连结AC,
∵四边形ABCD是菱形,
∴AC平分∠FAE,AD=AB=BC=CD.
∵CF⊥AF,CE⊥AE,
∴CF=CE,AF=AE.
∵AD=AB,
∴AFAD=AEAB,
∴DF=BE.
23.(满分9分) 如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.试探究四边形DAEF是平行四边形.
(1)四边形DAEF是矩形,△ABC满足?
(2)四边形DAEF是菱形,△ABC满足?
(3)ABC满足什么条件时,
以D,A,E,F为顶点的四边形不存在.
(1)证明:∵△ABD和△FBC都是等边三角形,
BD=BA,BF=BC,∠DBA=∠FBC=60°,
∴∠DBA∠FBA=∠FBC∠FBA,
∴∠DBF=∠ABC.
在△ABC和△DBF中,
∵
∴△ABC≌△DBF.
∴AC=DF=AE.
同理△ABC≌△EFC.
∴AB=EF=AD.
∴四边形ADFE是平行四边形.
解:当∠BAC=150°,∠DAE=360°-60°-60°-150°=90°,
∴平行四边形DAEF是矩形.
(2)当AB=AC≠BC,有AD=AE,
∴平行四边形DAEF是菱形.
当∠BAC=60°,△FBC与△ABC重合,故以D、A、E、F为顶点的四边形不存在.
24.(满分10分) (1)如图①,在正方形ABCD中,△APQ的顶点P,Q分别在BC,CD边上,
高AG与正方形的边长相等,求∠PAQ的度数;
(2)如图②,在Rt△ABC中,∠BAC=90°,AB=AC,点P,Q是BC边上的任意两点,且
∠PAQ=45°,请你探究BP,PQ, QC三条线段之间的数量关系,并说明理由;
(3)如图③,在△ABC中,∠BAC=45°,AD是边BC上的高,若BD=6,CD=4,则△ABC的面积为( )
解:(1)如图①:∵四边形ABCD是正方形,
∴∠BAD=∠B=∠C=∠D=90°,AB=BC=CD=DA
∵高AG与正方形的边长相等,
∴AG=AB,∠AGP=90°,
在Rt△ABP和Rt△AGP中,
AB=AG,AP=AP,
∴Rt△ABP≌△RtAGP,
∴∠BAP=∠GAP,
同理,∠GAQ=∠DAQ,
∴ ∠PAQ=∠BAD=×90°=45°;
(2)BP2=PQ2+QC2,
如图④,将△ABP绕点A逆时针旋转90°至△ACH位置,连接QH,
则有AH=AP,HC=BP, ∠HCA=∠B=∠C= 45°,
∴∠HCQ=∠HCA+∠ACB=45°+45°=90°.
∵∠BAP=∠CAH,∠PAQ=45°,
∴∠BAP+∠QAC=45°,
∴∠HAN=∠CAH+∠CAQ=∠BAP+∠QAC=45°,
∴∠PAQ=∠HAQ,
在△PAQ和△HAQ中,
∵
∴△PAQ≌△HAQ.
∴PQ=HQ.
在Rt△HCQ中
∴QH2=QC2+HC2,
∴BP2=PQ2+QC2;
(3)如图⑤,将△ABD沿AB折叠到△ABE的位置,将△ACD沿AC折叠到△ACF的位置,
延长EB、FC相交于点G,
则AD=AE=AF,∠E=∠F=∠ADB=90°.
∵∠BAC=45°,
∴∠EAF=2∠BAC=90°.
∴四边形AEGF矩形,
∵AE=AF,
∴矩形AEGF为正方形.
设正方形AEGF的边AE=x,
则BG=x6,GC=x4,
在Rt△BCG中,
BC2=BG2+GC2,
即(x6)2+(x4)2=102.
解得:x1=12,x2=2(舍去)
∴AD=AE=12.
∴S△ABC=BC·AD=×10×12=60.
25.(满分11分) 如图①,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)如图②,若∠1=70°,求∠MKN的度数;
(2)如图③,△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值.
25、解:(1)如图②,
∵四边形ABCD是矩形,
∴AM∥DN.
∴∠KNM=∠1.
∵∠1=70°,
∴∠KNM=∠KMN=∠1=70°,
∴∠MKN=40°.
(2)不能.理由如下:
如图③,过M点作ME⊥DN,垂足为E,则ME=AD=1.
∵∠KNM=∠KMN,
∴MK=NK,
又∵MK≥ME≥1,
∴NK≥1.
∴△MNK的面积=NK?ME≥.∴△MNK的面积不可能小于.
(3)分两种情况:
情况一:如图④,将矩形纸片对折,使点B与D重合,此时点K也与D重合.
MK=MB=x,则AM=5x.
由勾股定理得12+(5x)2=x2,
解得x=2.6.
∴MD=ND=2.6.
∴S△MNK=S△MND=1.3.
情况二:如图⑤,将矩形纸片沿对角线AC对折,此时折痕即为AC.
MK=AK=CK=x,则DK=5x.
同理可得MK=NK=2.6.
∵MD=1,
∴S△MNK==1.3.
△MNK的面积最大值为1.3.
26.(满分12分) 如图,在Rt△ABC中,∠B=90°,AC=72 cm,∠A=60°,点P从点C出发沿CA方向以6 cm/秒的速度向点A匀速运动,同时点Q从点A出发沿AB方向以3cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P,Q运动的时间是t秒(0<t≤12).过点P作PD⊥BC于点D,连结PQ,DQ.
(1)求证:AQ=PD;
(2)四边形APDQ能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)四边形PDBQ能够成为矩形吗?如果能,求出相应的t值,如果不能,说明理由.
(4)四边形PDBQ能够成为正方形吗?如果能,求出相应的t值,如果不能,说明理由.
26、 解:(1) ∵PD⊥BC,AB⊥BC,
∴∠CDP=∠B=90°,
∴PD∥AB,∠CPD=∠A=60°,
在Rt△CDP中,∠C=90°∠A=30°,CP=6t,
∴PD=3t,
又∵AQ=3t,
∴PD=AQ,
(2)能.理由:由(1)可得:PD∥AB,
∴PD=AQ,
∴四边形APDQ为平行四边形,
当AP=AQ时,四边形APDQ为菱形,
即726t=3t,解得t=8.
∴当t=8秒时,四边形AEFD为菱形
(3) 能.理由:由(1)可得:PD∥AB,
∠B=90°,
当PD=QB时,四边形PDBQ能够成为矩形.
即3t=363t,解得t=6.
(4)不能. 如果四边形PDBQ能够成为正方形,就有PD=PQ=AQ,
这是不可能的.
第24题图④
第21题图
第24题图⑤
第22题图
第24题图③
第21题图
第8题图
第9题图
第22题图
第23题图
第21题图
第25题图②
第24题图②
第6题图
第4题图
第24题图②
第24题图③
第23题图
第22题图
第24题图①
第12题图
第11题图
第20题图
第7题图
第25题图①
第24题图①
第26题图
第13题图
第15题图
第3题图
第16题图
第10题图
第14题图
第18题图
第25题图①
第25题图②
第25题图③
第25题图④
第25题图⑤
第26题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版2019-2020学年度下学期八年级数学(下册)
第5章特殊平行四边形检测题2(有答案)
(时间:100分钟 满分:120分)
题号 1 2 3 4 5 6 7 8 9 10
答案
一、选择题(共10小题 每3分 共30分)
1.下列说法中,错误的是( )
A. 对角线互相平分的四边形是平行四边形 B. 菱形的对角线互相垂直
C. 对角线相等且互相垂直的四边形是正方形 D. 对角线相等的平行四边形是矩形
2.已知菱形的周长为144cm,它的相邻的两个内角的比为1:2,则该菱形的较短的对角线的长为( )
A.48 B.36 C.32 D.24
3.如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有 ( )
A.4个 B.6个 C.8个 D.10个
4.在矩形 ABCDP中,长是4,宽是3,AC、BD是对角线,点P是AD上一动点,PE⊥AC于点
E,PF⊥BD于点F,则PE+PF等于( )
A.4? B.3.6 C.3 D.2.4
5.如图,在菱形ABCD中,点E是对角线BD上的一点,若BE=BC,EC=ED,则∠A的度数等于( )
A.72°? B.108° C.120° D.144°
6.如图,将正方形OABC放在平面直角坐标系中,O是坐标原点,点A的坐标为(3,5),则点B
的坐标为( )
A.(2,8)? B.(1,8) C.(2,3) D.(3,8)
7.如图,菱形纸片ABCD中,∠A=60°,菱形纸片ABCD沿着直线DE折叠(点E在边BC上),
使点C落在DP(P为AB中点)所在的直线上.则∠DEC的大小为( ).
A.50°?? B.55°? C.65°? D.75°
8.如图,已知点P为正方形ABCD内一点,且PA=PB=10cm,点P到边AD的距离也为10cm,
则正方形ABCD的对角线边长为( )cm.
A.16 B.16 C.8 D.8
9.已知,如图,过正方形ABCD的顶点C作对角线BD的平行线,在这条线上取一点E,使BE=BD连结DE,则∠CED的度数为( )
A.75° B.90° C.105° D.125°
10.如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交
于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:①△BDF≌△DCE;
②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD=AM2.其中正确结论的个数是( ?)
A.3? ? B.2?? ? C.1??? D.0
二、填空题(共10小题 每题3分 共30分)
11.将一正方形按如图方式分成n个全等矩形,上、下各横排两个,中间竖排若干个,则n的值为 .
12.如图,矩形ABCD中,AB=3,BC=4,点E为AD上的一动点,将△BAE沿BE向矩形的内部
折叠,若点A的对应点为 恰好落在∠BCD的平分线上时,则= .
13.如图,正方形DEFG内接于等边三角形ABC中,点D、E在BC边上,G、F分别在边AB和AC上,若等边三角形ABC的边长为(2+)cm,则正方形DEFG的面积为 .
14.如图,平面直角坐标系中,矩形OABC的顶点A(6,0),C(0,2).将矩形OABC绕点O
顺时针方向旋转,使点A恰好落在OB上的点A1处,若点B的对应点B1, 点C的对应点C1,
则直线B1C1的解析式为 .
15.如图,已知菱形ABCD的周长为12cm, AC=AB,点F、E分别在AB、BC上,过点F
作FG⊥DC于点G,连接FE,若∠EFG=15°,AF=1cm,则BE的等于 .
16.已知:如图,正方形ABCD的边长为8 cm,E在DC上,且DE=2 cm,P是AC上的一动点,则PD+PE的最小值为 .
17.已知一直角三角形的两边长恰为方程(2x+1)(x3)=(x+7)(x5)+20的两个根,则此直角三角形
斜边上的中线长是 .
18.如图,在矩形ABCD中,对角线长5,且∠1=∠2=∠3=∠4,则四边形EFGH的周长为 10 .
19.四边形ABCD的四条边分别为a、b、c、d,满足(a+b+c)2=3a2+3b2+3c2,3d=a+b+c,则四边
形形状为 ? .
20.如图,将△ADH绕点H顺时针旋转90°,点M、E的对应点分别为D、A,连结DM,△BCE
是△ADM沿 MA的方向平移到的,连结CD,CH,则有以下结论:①四边形ABCD是正方
形;②C、H、A三点,在一条直线上;③CE=DH;④若∠CHD=60°时,DM=2AM. .
三、解答题(共6题 共60分)
21.(满分9分) 如图,点E是矩形ABCD边上一点,AE=AD,AD>AB,过点D作DF⊥AE,垂足为点F,探究DF与AB的有和数量关系,并证明你的结论.
22.(满分9分)如图,已知四边形ABCD是菱形,点E、F分别是AB、AD延长线上的点,CE垂
直于AB的延长线于点E,CF垂直于AD延长线于点F,求证:DF=BE.
23.(满分9分) 如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.试探究四边形DAEF是平行四边形.
(1)四边形DAEF是矩形,△ABC满足?
(2)四边形DAEF是菱形,△ABC满足?
(3) △ABC满足什么条件时,
以D,A,E,F为顶点的四边形不存在.
24.(满分10分) (1)如图①,在正方形ABCD中,△APQ的顶点P,Q分别在BC,CD边上,
高AG与正方形的边长相等,求∠PAQ的度数;
(2)如图②,在Rt△ABC中,∠BAC=90°,AB=AC,点P,Q是BC边上的任意两点,且
∠PAQ=45°,请你探究BP,PQ, QC三条线段之间的数量关系,并说明理由;
(3)如图③,在△ABC中,∠BAC=45°,AD是边BC上的高,若BD=6,CD=4,则△ABC的面积为( )
25.(满分11分) 如图①,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)如图②,若∠1=70°,求∠MKN的度数;
(2)如图③,△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值.
26.(满分12分) 如图,在Rt△ABC中,∠B=90°,AC=72 cm,∠A=60°,点P从点C出发沿CA方向以6 cm/秒的速度向点A匀速运动,同时点Q从点A出发沿AB方向以3cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P,Q运动的时间是t秒(0<t≤12).过点P作PD⊥BC于点D,连结PQ,DQ.
(1)求证:AQ=PD;
(2)四边形APDQ能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)四边形PDBQ能够成为矩形吗?如果能,求出相应的t值,如果不能,说明理由.
(4)四边形PDBQ能够成为正方形吗?如果能,求出相应的t值,如果不能,说明理由.
参考答案
一、选择题(共10小题 每3分 共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D B A D A C A
二、填空题(共10小题 每题3分 共30分)
11、8 12、 13、3cm2 14、y= 15、 16、10cm
17、2.5或2 18、10 19、菱形或正方形 20、①②③④
三、解答题(共6题 共60分)
21.(满分9分) 如图,点E是矩形ABCD边上一点,AE=AD,AD>AB,过点D作DF⊥AE,垂足为点F,探究DF与AB的有和数量关系,并证明你的结论.
证明:DF=AB
∵四边形ABCD是矩形
∴AD//BC,∠C=90°,AB=CD?,
∴∠DAF=∠CED?,
∵AD=AE,
∴∠AED=∠DEC,
∴∠FED=∠CED.
∵DF⊥AE,
∴∠DFE=∠C=90°.
在△FDE和△CED中
∵
∴△FDE≌△CED
∴DF=CD
∴DF=AB.
22.(满分9分)如图,已知四边形ABCD是菱形,点E、F分别是AB、AD延长线上的点,CE垂
直于AB的延长线于点E,CF垂直于AD延长线于点F,求证:DF=BE.
证明:连结AC,
∵四边形ABCD是菱形,
∴AC平分∠FAE,AD=AB=BC=CD.
∵CF⊥AF,CE⊥AE,
∴CF=CE,AF=AE.
∵AD=AB,
∴AFAD=AEAB,
∴DF=BE.
23.(满分9分) 如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.试探究四边形DAEF是平行四边形.
(1)四边形DAEF是矩形,△ABC满足?
(2)四边形DAEF是菱形,△ABC满足?
(3)ABC满足什么条件时,
以D,A,E,F为顶点的四边形不存在.
(1)证明:∵△ABD和△FBC都是等边三角形,
BD=BA,BF=BC,∠DBA=∠FBC=60°,
∴∠DBA∠FBA=∠FBC∠FBA,
∴∠DBF=∠ABC.
在△ABC和△DBF中,
∵
∴△ABC≌△DBF.
∴AC=DF=AE.
同理△ABC≌△EFC.
∴AB=EF=AD.
∴四边形ADFE是平行四边形.
解:当∠BAC=150°,∠DAE=360°-60°-60°-150°=90°,
∴平行四边形DAEF是矩形.
(2)当AB=AC≠BC,有AD=AE,
∴平行四边形DAEF是菱形.
当∠BAC=60°,△FBC与△ABC重合,故以D、A、E、F为顶点的四边形不存在.
24.(满分10分) (1)如图①,在正方形ABCD中,△APQ的顶点P,Q分别在BC,CD边上,
高AG与正方形的边长相等,求∠PAQ的度数;
(2)如图②,在Rt△ABC中,∠BAC=90°,AB=AC,点P,Q是BC边上的任意两点,且
∠PAQ=45°,请你探究BP,PQ, QC三条线段之间的数量关系,并说明理由;
(3)如图③,在△ABC中,∠BAC=45°,AD是边BC上的高,若BD=6,CD=4,则△ABC的面积为( )
解:(1)如图①:∵四边形ABCD是正方形,
∴∠BAD=∠B=∠C=∠D=90°,AB=BC=CD=DA
∵高AG与正方形的边长相等,
∴AG=AB,∠AGP=90°,
在Rt△ABP和Rt△AGP中,
AB=AG,AP=AP,
∴Rt△ABP≌△RtAGP,
∴∠BAP=∠GAP,
同理,∠GAQ=∠DAQ,
∴ ∠PAQ=∠BAD=×90°=45°;
(2)BP2=PQ2+QC2,
如图④,将△ABP绕点A逆时针旋转90°至△ACH位置,连接QH,
则有AH=AP,HC=BP, ∠HCA=∠B=∠C= 45°,
∴∠HCQ=∠HCA+∠ACB=45°+45°=90°.
∵∠BAP=∠CAH,∠PAQ=45°,
∴∠BAP+∠QAC=45°,
∴∠HAN=∠CAH+∠CAQ=∠BAP+∠QAC=45°,
∴∠PAQ=∠HAQ,
在△PAQ和△HAQ中,
∵
∴△PAQ≌△HAQ.
∴PQ=HQ.
在Rt△HCQ中
∴QH2=QC2+HC2,
∴BP2=PQ2+QC2;
(3)如图⑤,将△ABD沿AB折叠到△ABE的位置,将△ACD沿AC折叠到△ACF的位置,
延长EB、FC相交于点G,
则AD=AE=AF,∠E=∠F=∠ADB=90°.
∵∠BAC=45°,
∴∠EAF=2∠BAC=90°.
∴四边形AEGF矩形,
∵AE=AF,
∴矩形AEGF为正方形.
设正方形AEGF的边AE=x,
则BG=x6,GC=x4,
在Rt△BCG中,
BC2=BG2+GC2,
即(x6)2+(x4)2=102.
解得:x1=12,x2=2(舍去)
∴AD=AE=12.
∴S△ABC=BC·AD=×10×12=60.
25.(满分11分) 如图①,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)如图②,若∠1=70°,求∠MKN的度数;
(2)如图③,△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值.
25、解:(1)如图②,
∵四边形ABCD是矩形,
∴AM∥DN.
∴∠KNM=∠1.
∵∠1=70°,
∴∠KNM=∠KMN=∠1=70°,
∴∠MKN=40°.
(2)不能.理由如下:
如图③,过M点作ME⊥DN,垂足为E,则ME=AD=1.
∵∠KNM=∠KMN,
∴MK=NK,
又∵MK≥ME≥1,
∴NK≥1.
∴△MNK的面积=NK?ME≥.∴△MNK的面积不可能小于.
(3)分两种情况:
情况一:如图④,将矩形纸片对折,使点B与D重合,此时点K也与D重合.
MK=MB=x,则AM=5x.
由勾股定理得12+(5x)2=x2,
解得x=2.6.
∴MD=ND=2.6.
∴S△MNK=S△MND=1.3.
情况二:如图⑤,将矩形纸片沿对角线AC对折,此时折痕即为AC.
MK=AK=CK=x,则DK=5x.
同理可得MK=NK=2.6.
∵MD=1,
∴S△MNK==1.3.
△MNK的面积最大值为1.3.
26.(满分12分) 如图,在Rt△ABC中,∠B=90°,AC=72 cm,∠A=60°,点P从点C出发沿CA方向以6 cm/秒的速度向点A匀速运动,同时点Q从点A出发沿AB方向以3cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P,Q运动的时间是t秒(0<t≤12).过点P作PD⊥BC于点D,连结PQ,DQ.
(1)求证:AQ=PD;
(2)四边形APDQ能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)四边形PDBQ能够成为矩形吗?如果能,求出相应的t值,如果不能,说明理由.
(4)四边形PDBQ能够成为正方形吗?如果能,求出相应的t值,如果不能,说明理由.
26、 解:(1) ∵PD⊥BC,AB⊥BC,
∴∠CDP=∠B=90°,
∴PD∥AB,∠CPD=∠A=60°,
在Rt△CDP中,∠C=90°∠A=30°,CP=6t,
∴PD=3t,
又∵AQ=3t,
∴PD=AQ,
(2)能.理由:由(1)可得:PD∥AB,
∴PD=AQ,
∴四边形APDQ为平行四边形,
当AP=AQ时,四边形APDQ为菱形,
即726t=3t,解得t=8.
∴当t=8秒时,四边形AEFD为菱形
(3) 能.理由:由(1)可得:PD∥AB,
∠B=90°,
当PD=QB时,四边形PDBQ能够成为矩形.
即3t=363t,解得t=6.
(4)不能. 如果四边形PDBQ能够成为正方形,就有PD=PQ=AQ,
这是不可能的.
第24题图④
第21题图
第24题图⑤
第22题图
第24题图③
第21题图
第8题图
第9题图
第22题图
第23题图
第21题图
第25题图②
第24题图②
第6题图
第4题图
第24题图②
第24题图③
第23题图
第22题图
第24题图①
第12题图
第11题图
第20题图
第7题图
第25题图①
第24题图①
第26题图
第13题图
第15题图
第3题图
第16题图
第10题图
第14题图
第18题图
第25题图①
第25题图②
第25题图③
第25题图④
第25题图⑤
第26题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
