6.1.2 反比例函数的表达式(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 6.1.2 反比例函数的表达式(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 466.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.1
反比例函数
第2课时
反比例函数的表达式
【知识清单】
一、待定系数法求反比例函数的表达式:
用待定系数法求反比例函数解析式的一般步骤:?
1.确定含有待定系数的反比例函数的解析式,y=
(k≠0);
2.将自变量和函数的对应值代入含有待定系数的解析式中,求出待定系数k;
3.把求出的待定系数k的值带入到解析式中,求出函数的解析式.
二、求实际问题中反比例函数的表达式:
1.理清实际问题中变量之间的对应关系,建立反比例函数模型,确定含有待定系数的反比例函数的解析式,然后将变量的一组对应值代入,进而解决问题;
2.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力.
【经典例题】
例题1、对于函数y=,若x=2时,y=,则这个函数的解析式是( )
A.y=
B.y=
C.y=
D.y=
【考点】反比例函数的表达式.
【分析】根据题意设出反比例函数的解析式y=
(k≠0),将x=2时,y=代入y=中,确定k的即可求解.
【解答】设反比例函数的解析式为y=,
把x=2时,y=,代入解析式y=,
解得k=,
则反比例函数的解析式是y=.
故选C.
【点评】主要考查学生对“初中求反比例函数的解析式及反比例函数的应用”相关知识的理解.理解反比例函数的定义和正确代入求待定系数k是解决问题的关键.
例题2、已知y=y2y1,y1与x2成正比例,y2与2x1成反比例,当x=0时,y=4;当x=1时,y=5.
(1)求y与x的函数关系式;
(2)当x=3时,求y的值.
【考点】待定系数法求函数解析式.
【分析】?(1)根据题意,可设y1=k1(x2),y2=;代入数据可得关于k1,k2的二元一次方程组,求出k1,k2的值即可得出答案;
(2)将x=3代入由(1)可得解析式中,求值即可.
【解答】(1)y1=k1(x2),y2=;
则有:y=y2y1=k1(x2).
∵当x=0时,y=7;当x=1时,y=5时.
∴可得,
解得:k1=2,k2=3.
所以y与x的函数关系式为:y=;
(2)把x=3代入y==.
【点评】本题考查待定系数法的运用,关键是根据题意设出关系式,再代入数据求出未知系数即可.
【夯实基础】
1、已知变量x、y满足下面的关系:则x,y之间用关系式表示为( )
x
…
6
8
12
12
8
6
…
y
…
2
1.5
1
1
1.5
2
…
A.y=???
B.y=???
C.y=??
??D.y=
2、已知函数y=?,当x=5时,函数值等于2,则m的值是( )
A.?4???
B.?4???
C.???
??D.?
3、某沼泽地能承受的压强为20
000
Pa,一位同学的体重为600
N,为了让他不陷入沼泽地,他与沼泽地的接触面积至少为( )
A.0.01
m2
B.3
m2
C.0.1
m2
D.0.03
m2
4、小颖根据下表,作了三个推测:
x
…
1
10
100
1000
10000
…
5+
…
4
3.1
3.01
3.001
3.0001
…
①5+(x>0)的值随着x的增大越来越小;
②5+(x>0)的值有可能等于3;
③5+(x>0)的值随着x的增大越来越接近于3.
则推测正确的有( )
A.0个
B.1个
C.2个
D.3个
5、在某一电路中,保持电压不变,电流I(单位:A)与电阻R(单位:Ω)成反比例,当电阻R=15Ω时,电流I=3A.则I与R之间的函数关系式
,当电流为15A时,电阻应是
.
6、(1)已知函数y=y1+y2,其中y1与x2成反比例,且比例系数为k1;y2与x3成正比例,且比例系数为k2;当x=1时,y=2
,那么k1与k2数量关系的表达式为
;(2)一个对角线相互垂直的四边形的面积为7cm2,对角线的长分别为x(cm),y(cm),则x与y的解析式为
.
7、已知变量y1与x22成反比例,且当x=2时y=3.
(1)写出y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当x=时,求y的值;
(3)当y=7时,求x的值.
8、面积一定的梯形,其上底是下底的五分之一,且当下底x=15cm时,高y=9cm,
问(1)求x与y的函数表达式;
(2)当y=3cm时,下底长是多少?
9、某品牌的运动装每套的进价为240元,为寻求合适的销售价格进行了4天的试销,试销情况如
表所示:
第1天
第2天
第3天
第4天
售价x(元/套)
300
400
500
600
销售量y(套)
20
15
12
10
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
【提优特训】
10、若x=2时,正比例函数y=k1x(k1≠0)
与反比例函数y=(k2≠0)的值相等,则k1:k2的值.
A.2:1
B.4:1
C.1:2
D.1:4
11、若y与5x+1成正比例,x与成正比例,则y是z的( )
A.正比例函数
B.反比例函数
C.一次函数
D.不能确定
12、反比例函数(k≠0,k为常数)当自变量x的值从1增加到2,函数值就减少了3,则k的
值为(
)
A.6???????
?
?B.6??????
??
?
C.3????
?
???D.3
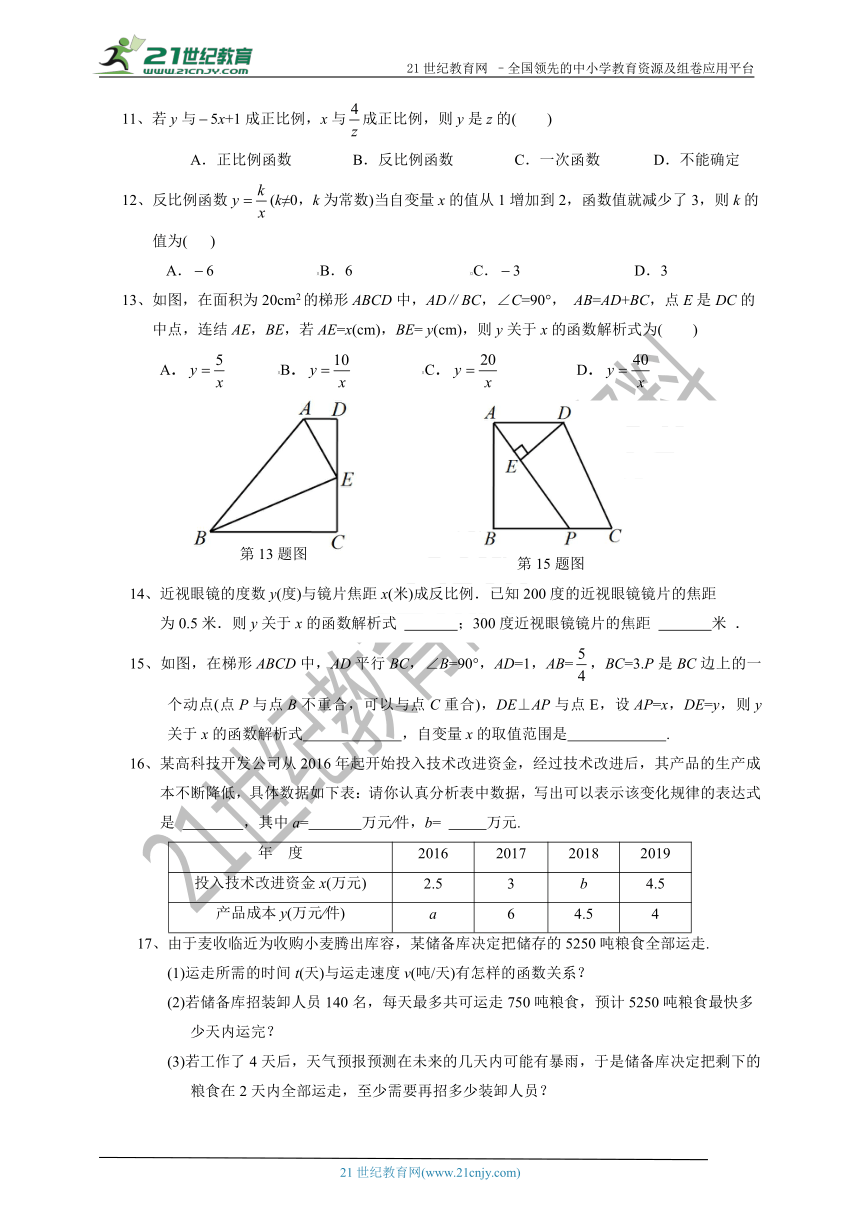
13、如图,在面积为20cm2的梯形ABCD中,AD∥BC,∠C=90°,
AB=AD+BC,点E是DC的
中点,连结AE,BE,若AE=x(cm),BE=
y(cm),则y关于x的函数解析式为( )
A.????????
?B.????????
C.?????
???D.
14、近视眼镜的度数y(度)与镜片焦距x(米)成反比例.已知200度的近视眼镜镜片的焦距
为0.5米.则y关于x的函数解析式
;300度近视眼镜镜片的焦距
米
.
15、如图,在梯形ABCD中,AD平行BC,∠B=90°,AD=1,AB=,BC=3.P是BC边上的一个动点(点P与点B不重合,可以与点C重合),DE⊥AP与点E,设AP=x,DE=y,则y关于x的函数解析式
,自变量x的取值范围是
.
16、某高科技开发公司从2016年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
,其中a=
万元∕件,b=
万元.
年????度
2016
2017
2018
2019
投入技术改进资金x(万元)
2.5
3
b
4.5
产品成本y(万元∕件)
a
6
4.5
4
17、由于麦收临近为收购小麦腾出库容,某储备库决定把储存的5250吨粮食全部运走.
(1)运走所需的时间t(天)与运走速度v(吨/天)有怎样的函数关系?
(2)若储备库招装卸人员140名,每天最多共可运走750吨粮食,预计5250吨粮食最快多
少天内运完?
(3)若工作了4天后,天气预报预测在未来的几天内可能有暴雨,于是储备库决定把剩下的
粮食在2天内全部运走,至少需要再招多少装卸人员?
18、在面积为定值的一组菱形中,当菱形的一条对角线长为6时,它的另一条对角线长为10.
(1)设菱形的两条对角线的长分别为x,y,求y关于x的函数解析式;
(2)若其中一个菱形的一条对角线长为12,这个菱形的边长;
(3)当(1)中的x为何值时,这个四边形是正方形?
?
?
【中考链接】
19、(2018?柳州)已知反比例函数的解析式为y=,则a的取值范围是( )
A.a≠2
B.a≠﹣2
C.a≠±2
D.a=±2
20、(2019?天津北辰一模)已知反比例函数y=(k≠0),当自变量
x满足时,对应的函数值y满足;则k的取值为(
)
A.
B.
C.2
D.4
参考答案
1、C
2、B
3、D
4、C
5、,3Ω
6、k14k2=2,
10、D
11、C
12、B
13、C
14、,
15、
,
16、
,a=7.2,b=4
19、C
20、A
7、已知变量y1与x22成反比例,且当x=2时y=3.
(1)写出y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当x=时,求y的值;
(3)当y=7时,求x的值.
解:(1)设所求函数解析式为y
1=,即y=+1,
把x=2时y=3代入y=+1得,3=,
解得:k=8,
∴函数解析式为y=+1,
∵x22=0时,
没有意义,
∴x2≠2,解得x≠,
∴自变量x的取值范围x≠;
(2)当x=时,
y=+1=1;
(3)当y=
7时,7=+1,
解得x=.
8、面积一定的梯形,其上底是下底的五分之一,且当下底x=15cm时,高y=9cm,
问(1)求x与y的函数表达式;
(2)当y=3cm时,下底长是多少?
解:(1)根据题意,得上底=,
面积=×(+x)y
因为面积一定,根据给出的一组已知数量,可以求得面积=×(3+15)
×9
=81平方厘米
所以又81=×(+x)y
解得y=
(2)当y=3cm时,x=45cm.
9、某品牌的运动装每套的进价为240元,为寻求合适的销售价格进行了4天的试销,试销情况如
表所示:
第1天
第2天
第3天
第4天
售价x(元/套)
300
400
500
600
销售量y(套)
20
15
12
10
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
解:(1)由表中数据得:xy=6000,
∴y=,
∴y是x的反比例函数,
故所求函数关系式为y=;
(2)由题意得:(x240)y=3000,
把y=代入得:(x240)?=3000,
解得:x=480;
经检验,x=480是原方程的根;
答:若商场计划每天的销售利润为3000元,则其单价应定为480元.
17、由于麦收临近为收购小麦腾出库容,某储备库决定把储存的5250吨粮食全部运走.
(1)运走所需的时间t(天)与运走速度v(吨/天)有怎样的函数关系?
(2)若储备库招装卸人员140名,每天最多共可运走750吨粮食,预计5250吨粮食最快多
少天内运完?
(3)若工作了4天后,天气预报预测在未来的几天内可能有暴雨,于是储备库决定把剩下的
粮食在2天内全部运走,至少需要再招多少装卸人员?
解:(1)根据题意,得;
(2)当v=750时,=7,
5250吨粮食最快7天内运完.
(3)设需要再招装卸人员x人,
根据题意,得2×(140+x)×=52504×750
解得x=70(人).
答:至少需要再招70名装卸人员.
18、在面积为定值的一组菱形中,当菱形的一条对角线长为6时,它的另一条对角线长为10.
(1)设菱形的两条对角线的长分别为x,y,求y关于x的函数解析式;
(2)若其中一个菱形的一条对角线长为12,这个菱形的边长;
(3)当(1)中的x为何值时,这个四边形是正方形?
?解:(1)∵在面积为定值的一组菱形中,当菱形的一条对角线长为5时,
它的另一条对角线长为8,
∴S菱形=×6×10=30,
∵菱形的两条对角线的长分别为x,y,
∴S菱形=xy=30,
∴y关于x的函数解析式为:y=;
(2)∵其中一个菱形的一条对角线长为12,
∴另一条对角线长为:60÷12=5,
∴这个菱形的边长为:;
(3)∵当对角线相等时,这个四边形是正方形,
∴x2=30,
解得:x=,
∴当x=时,这个四边形是正方形.
?
第15题图
第13题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.1
反比例函数
第2课时
反比例函数的表达式
【知识清单】
一、待定系数法求反比例函数的表达式:
用待定系数法求反比例函数解析式的一般步骤:?
1.确定含有待定系数的反比例函数的解析式,y=
(k≠0);
2.将自变量和函数的对应值代入含有待定系数的解析式中,求出待定系数k;
3.把求出的待定系数k的值带入到解析式中,求出函数的解析式.
二、求实际问题中反比例函数的表达式:
1.理清实际问题中变量之间的对应关系,建立反比例函数模型,确定含有待定系数的反比例函数的解析式,然后将变量的一组对应值代入,进而解决问题;
2.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力.
【经典例题】
例题1、对于函数y=,若x=2时,y=,则这个函数的解析式是( )
A.y=
B.y=
C.y=
D.y=
【考点】反比例函数的表达式.
【分析】根据题意设出反比例函数的解析式y=
(k≠0),将x=2时,y=代入y=中,确定k的即可求解.
【解答】设反比例函数的解析式为y=,
把x=2时,y=,代入解析式y=,
解得k=,
则反比例函数的解析式是y=.
故选C.
【点评】主要考查学生对“初中求反比例函数的解析式及反比例函数的应用”相关知识的理解.理解反比例函数的定义和正确代入求待定系数k是解决问题的关键.
例题2、已知y=y2y1,y1与x2成正比例,y2与2x1成反比例,当x=0时,y=4;当x=1时,y=5.
(1)求y与x的函数关系式;
(2)当x=3时,求y的值.
【考点】待定系数法求函数解析式.
【分析】?(1)根据题意,可设y1=k1(x2),y2=;代入数据可得关于k1,k2的二元一次方程组,求出k1,k2的值即可得出答案;
(2)将x=3代入由(1)可得解析式中,求值即可.
【解答】(1)y1=k1(x2),y2=;
则有:y=y2y1=k1(x2).
∵当x=0时,y=7;当x=1时,y=5时.
∴可得,
解得:k1=2,k2=3.
所以y与x的函数关系式为:y=;
(2)把x=3代入y==.
【点评】本题考查待定系数法的运用,关键是根据题意设出关系式,再代入数据求出未知系数即可.
【夯实基础】
1、已知变量x、y满足下面的关系:则x,y之间用关系式表示为( )
x
…
6
8
12
12
8
6
…
y
…
2
1.5
1
1
1.5
2
…
A.y=???
B.y=???
C.y=??
??D.y=
2、已知函数y=?,当x=5时,函数值等于2,则m的值是( )
A.?4???
B.?4???
C.???
??D.?
3、某沼泽地能承受的压强为20
000
Pa,一位同学的体重为600
N,为了让他不陷入沼泽地,他与沼泽地的接触面积至少为( )
A.0.01
m2
B.3
m2
C.0.1
m2
D.0.03
m2
4、小颖根据下表,作了三个推测:
x
…
1
10
100
1000
10000
…
5+
…
4
3.1
3.01
3.001
3.0001
…
①5+(x>0)的值随着x的增大越来越小;
②5+(x>0)的值有可能等于3;
③5+(x>0)的值随着x的增大越来越接近于3.
则推测正确的有( )
A.0个
B.1个
C.2个
D.3个
5、在某一电路中,保持电压不变,电流I(单位:A)与电阻R(单位:Ω)成反比例,当电阻R=15Ω时,电流I=3A.则I与R之间的函数关系式
,当电流为15A时,电阻应是
.
6、(1)已知函数y=y1+y2,其中y1与x2成反比例,且比例系数为k1;y2与x3成正比例,且比例系数为k2;当x=1时,y=2
,那么k1与k2数量关系的表达式为
;(2)一个对角线相互垂直的四边形的面积为7cm2,对角线的长分别为x(cm),y(cm),则x与y的解析式为
.
7、已知变量y1与x22成反比例,且当x=2时y=3.
(1)写出y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当x=时,求y的值;
(3)当y=7时,求x的值.
8、面积一定的梯形,其上底是下底的五分之一,且当下底x=15cm时,高y=9cm,
问(1)求x与y的函数表达式;
(2)当y=3cm时,下底长是多少?
9、某品牌的运动装每套的进价为240元,为寻求合适的销售价格进行了4天的试销,试销情况如
表所示:
第1天
第2天
第3天
第4天
售价x(元/套)
300
400
500
600
销售量y(套)
20
15
12
10
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
【提优特训】
10、若x=2时,正比例函数y=k1x(k1≠0)
与反比例函数y=(k2≠0)的值相等,则k1:k2的值.
A.2:1
B.4:1
C.1:2
D.1:4
11、若y与5x+1成正比例,x与成正比例,则y是z的( )
A.正比例函数
B.反比例函数
C.一次函数
D.不能确定
12、反比例函数(k≠0,k为常数)当自变量x的值从1增加到2,函数值就减少了3,则k的
值为(
)
A.6???????
?
?B.6??????
??
?
C.3????
?
???D.3
13、如图,在面积为20cm2的梯形ABCD中,AD∥BC,∠C=90°,
AB=AD+BC,点E是DC的
中点,连结AE,BE,若AE=x(cm),BE=
y(cm),则y关于x的函数解析式为( )
A.????????
?B.????????
C.?????
???D.
14、近视眼镜的度数y(度)与镜片焦距x(米)成反比例.已知200度的近视眼镜镜片的焦距
为0.5米.则y关于x的函数解析式
;300度近视眼镜镜片的焦距
米
.
15、如图,在梯形ABCD中,AD平行BC,∠B=90°,AD=1,AB=,BC=3.P是BC边上的一个动点(点P与点B不重合,可以与点C重合),DE⊥AP与点E,设AP=x,DE=y,则y关于x的函数解析式
,自变量x的取值范围是
.
16、某高科技开发公司从2016年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
,其中a=
万元∕件,b=
万元.
年????度
2016
2017
2018
2019
投入技术改进资金x(万元)
2.5
3
b
4.5
产品成本y(万元∕件)
a
6
4.5
4
17、由于麦收临近为收购小麦腾出库容,某储备库决定把储存的5250吨粮食全部运走.
(1)运走所需的时间t(天)与运走速度v(吨/天)有怎样的函数关系?
(2)若储备库招装卸人员140名,每天最多共可运走750吨粮食,预计5250吨粮食最快多
少天内运完?
(3)若工作了4天后,天气预报预测在未来的几天内可能有暴雨,于是储备库决定把剩下的
粮食在2天内全部运走,至少需要再招多少装卸人员?
18、在面积为定值的一组菱形中,当菱形的一条对角线长为6时,它的另一条对角线长为10.
(1)设菱形的两条对角线的长分别为x,y,求y关于x的函数解析式;
(2)若其中一个菱形的一条对角线长为12,这个菱形的边长;
(3)当(1)中的x为何值时,这个四边形是正方形?
?
?
【中考链接】
19、(2018?柳州)已知反比例函数的解析式为y=,则a的取值范围是( )
A.a≠2
B.a≠﹣2
C.a≠±2
D.a=±2
20、(2019?天津北辰一模)已知反比例函数y=(k≠0),当自变量
x满足时,对应的函数值y满足;则k的取值为(
)
A.
B.
C.2
D.4
参考答案
1、C
2、B
3、D
4、C
5、,3Ω
6、k14k2=2,
10、D
11、C
12、B
13、C
14、,
15、
,
16、
,a=7.2,b=4
19、C
20、A
7、已知变量y1与x22成反比例,且当x=2时y=3.
(1)写出y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当x=时,求y的值;
(3)当y=7时,求x的值.
解:(1)设所求函数解析式为y
1=,即y=+1,
把x=2时y=3代入y=+1得,3=,
解得:k=8,
∴函数解析式为y=+1,
∵x22=0时,
没有意义,
∴x2≠2,解得x≠,
∴自变量x的取值范围x≠;
(2)当x=时,
y=+1=1;
(3)当y=
7时,7=+1,
解得x=.
8、面积一定的梯形,其上底是下底的五分之一,且当下底x=15cm时,高y=9cm,
问(1)求x与y的函数表达式;
(2)当y=3cm时,下底长是多少?
解:(1)根据题意,得上底=,
面积=×(+x)y
因为面积一定,根据给出的一组已知数量,可以求得面积=×(3+15)
×9
=81平方厘米
所以又81=×(+x)y
解得y=
(2)当y=3cm时,x=45cm.
9、某品牌的运动装每套的进价为240元,为寻求合适的销售价格进行了4天的试销,试销情况如
表所示:
第1天
第2天
第3天
第4天
售价x(元/套)
300
400
500
600
销售量y(套)
20
15
12
10
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
解:(1)由表中数据得:xy=6000,
∴y=,
∴y是x的反比例函数,
故所求函数关系式为y=;
(2)由题意得:(x240)y=3000,
把y=代入得:(x240)?=3000,
解得:x=480;
经检验,x=480是原方程的根;
答:若商场计划每天的销售利润为3000元,则其单价应定为480元.
17、由于麦收临近为收购小麦腾出库容,某储备库决定把储存的5250吨粮食全部运走.
(1)运走所需的时间t(天)与运走速度v(吨/天)有怎样的函数关系?
(2)若储备库招装卸人员140名,每天最多共可运走750吨粮食,预计5250吨粮食最快多
少天内运完?
(3)若工作了4天后,天气预报预测在未来的几天内可能有暴雨,于是储备库决定把剩下的
粮食在2天内全部运走,至少需要再招多少装卸人员?
解:(1)根据题意,得;
(2)当v=750时,=7,
5250吨粮食最快7天内运完.
(3)设需要再招装卸人员x人,
根据题意,得2×(140+x)×=52504×750
解得x=70(人).
答:至少需要再招70名装卸人员.
18、在面积为定值的一组菱形中,当菱形的一条对角线长为6时,它的另一条对角线长为10.
(1)设菱形的两条对角线的长分别为x,y,求y关于x的函数解析式;
(2)若其中一个菱形的一条对角线长为12,这个菱形的边长;
(3)当(1)中的x为何值时,这个四边形是正方形?
?解:(1)∵在面积为定值的一组菱形中,当菱形的一条对角线长为5时,
它的另一条对角线长为8,
∴S菱形=×6×10=30,
∵菱形的两条对角线的长分别为x,y,
∴S菱形=xy=30,
∴y关于x的函数解析式为:y=;
(2)∵其中一个菱形的一条对角线长为12,
∴另一条对角线长为:60÷12=5,
∴这个菱形的边长为:;
(3)∵当对角线相等时,这个四边形是正方形,
∴x2=30,
解得:x=,
∴当x=时,这个四边形是正方形.
?
第15题图
第13题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
