6.2.1 反比例函数的图象和性质(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 6.2.1 反比例函数的图象和性质(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 751.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 16:34:34 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.2
反比例函数的图象和性质
第1课时
反比例函数的图象和性质(1)
【知识清单】
1.反比例函数(k≠0)的图象是由两个分支组成的曲线.当k>0时,图象在一、三象限;当k<0时,图象在二、四象限.
2.反比例函数(k≠0)的图象关于直角坐标系的原点成中心对称.
【经典例题】
例题1、若反比例函数的图象位于第二、四象限内,则m的取值范围是( )
A.m>0
B.m<5
C.m>5
D.m<12
【考点】反比例函数的图象和性质.
【分析】根据反比例函数性质:图象位于第二、四象限内,则有k<0,即153m<0,解出m即可.
【解答】根据题意,得153m<0,
解得m>5.
故选C.
【点评】本题主要目的是检查学生对于考点“反比例函数的性质”相关知识的理解.熟练掌握反比例函数的性质是解决问题的关键.
例题2、如图是反比例函数(k>0)的图象在第一象限的部分曲线,P为曲线上任意一点,PM垂直x轴于点M,求△OPM的面积(用用含k的代数式表示).
【考点】反比例函数的图象和性质.
【分析】?设出点P的坐标(x,y),则有△OPM的面积等于点P的纵横坐标的绝对值的积的一半,然后把相关数据代入即可.
【解答】设点P的坐标为(x,y).
∵P(x,y)在第一象限,且在反比例函数(k>0)的图象上,
∴6k=xy,
∴△OPM的面积=xy=×6k=3k.
【点评】本题考查了反比例函数中的k的意义,用到的知识点为,在反比例函数图象的点坐标的绝对值的积等于反比例函数系数的绝对值.
【夯实基础】
1、下列图形中阴影部分面积相等的是(
)
A.①②
B.②③
C.①④
D.③④
2、下列各点中,在反比例函数y=图象上的是(
)
A.
B.
C.
D.
3、反比例函数y=、y=、y=的共同点是(
)
A.图象位于同样的象限
B.自变量的取值范围是任意实数
C.图象关于直角坐标系的原点成中心对称
D.图象可以与坐标轴相交
4、若反比例函数y=的图象在一、三象限,则函数y=axb的图象一定经过的象限为(
)
A.一、三象限
B.二、三象限
C.一、四象限
D.三、四象限
5、若反比例函数y=(m≤5)的图象在一、三象限,则m的取值范围是
.若一次函数y=ax+b的图象不经过第三象限,则反比例函数y=的图象
象限.
6、在平面直角坐标系xOy中,点A(a<0,b<0)在反比例函数y=图象上.点A关于y轴的对称点B在双曲线y=上,则m+n的值为
.
7、已知反比例函数y=(k≠0)的图象的一个分支如图所示,请画出它的另一个分支.
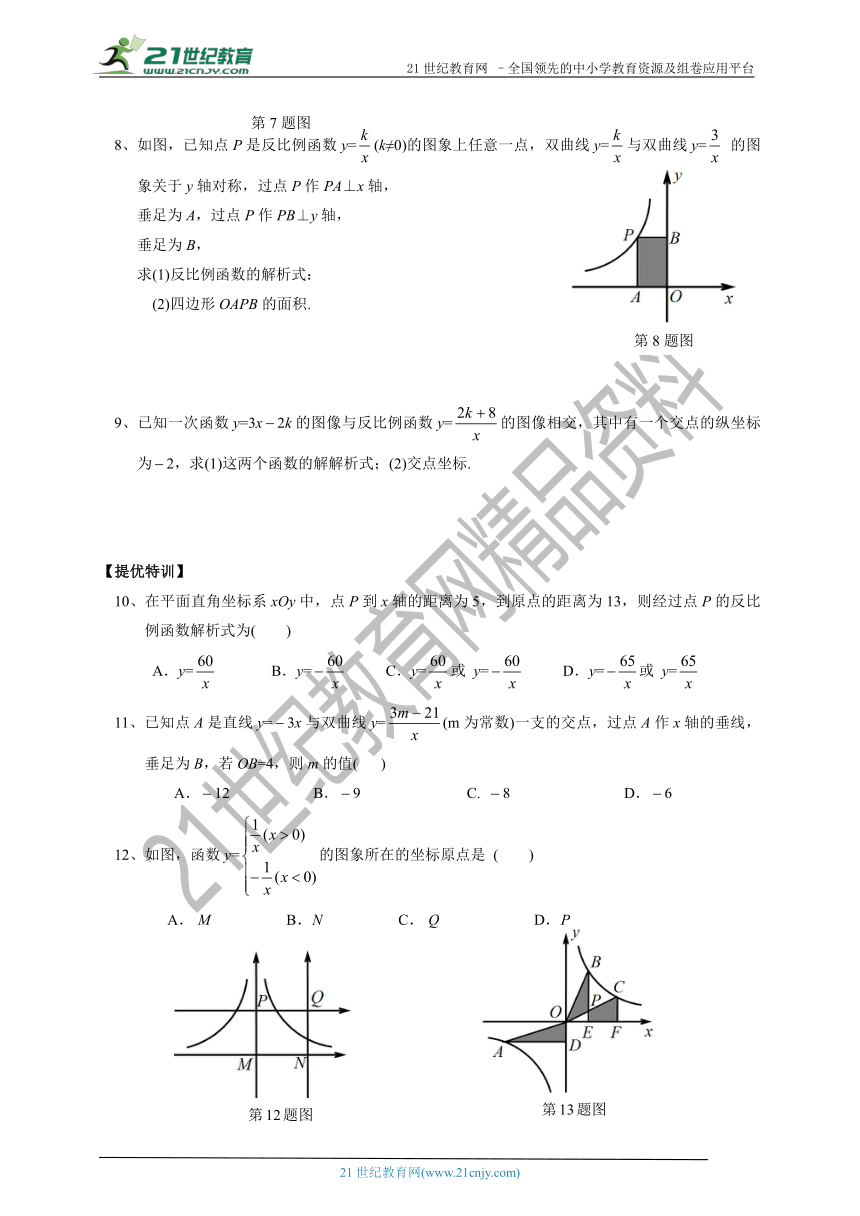
8、如图,已知点P是反比例函数y=(k≠0)的图象上任意一点,双曲线y=与双曲线y=
的图象关于y轴对称,过点P作PA⊥x轴,
垂足为A,过点P作PB⊥y轴,
垂足为B,
求(1)反比例函数的解析式:
(2)四边形OAPB的面积.
9、已知一次函数y=3x2k的图像与反比例函数y=的图像相交,其中有一个交点的纵坐标为2,求(1)这两个函数的解解析式;(2)交点坐标.
【提优特训】
10、在平面直角坐标系xOy中,点P到x轴的距离为5,到原点的距离为13,则经过点P的反比例函数解析式为( )
A.y=
B.y=
C.y=或
y=
D.y=或
y=
11、已知点A是直线y=3x与双曲线y=(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,若OB=4,则m的值(
)
A.12
B.9
C.
8
D.6
12、如图,函数y=的图象所在的坐标原点是
( )
A.?M?????
???B.N?????????
?C.?Q?????
??D.P
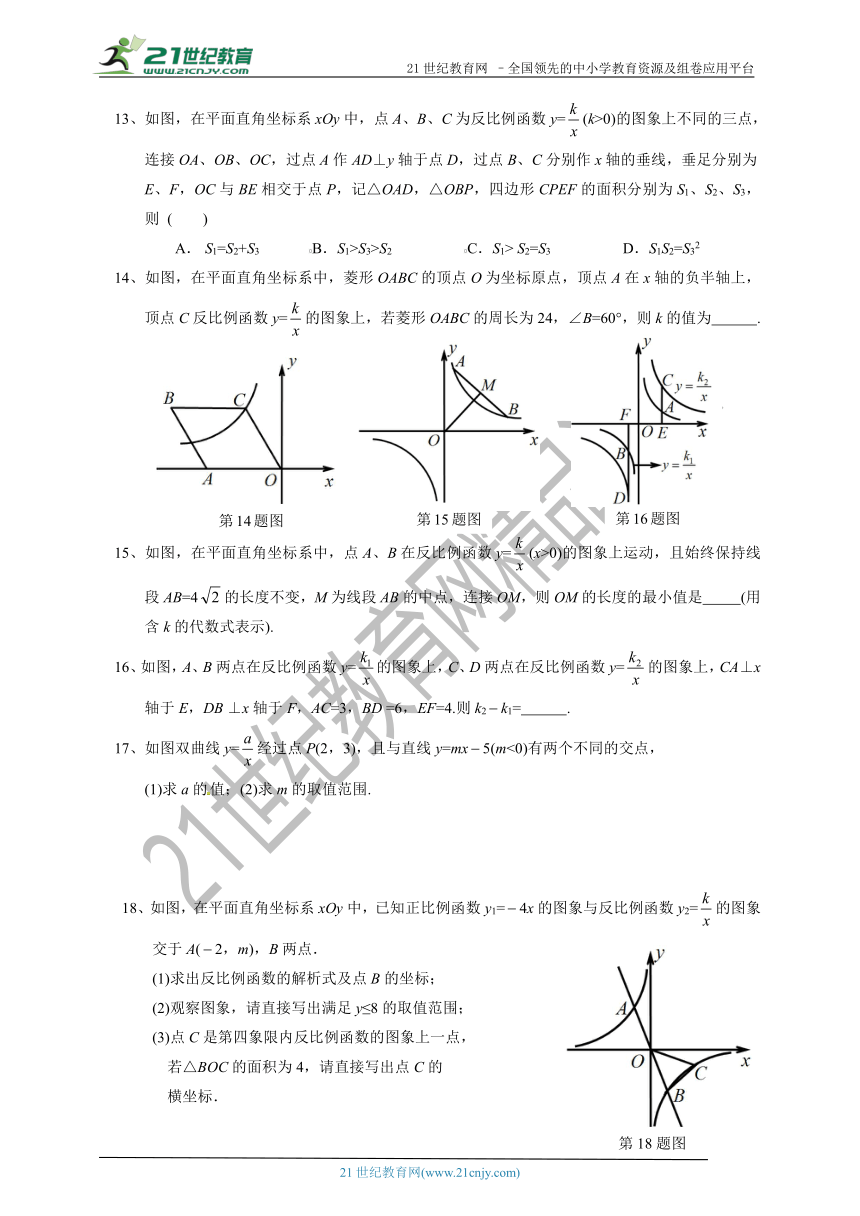
13、如图,在平面直角坐标系xOy中,点A、B、C为反比例函数y=(k>0)的图象上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作x轴的垂线,垂足分别为E、F,OC与BE相交于点P,记△OAD,△OBP,四边形CPEF的面积分别为S1、S2、S3,则
( )
A.?S1=S2+S3????????
?B.S1>S3>S2????????
?
C.S1>?S2=S3????
???D.S1S2=S32
14、如图,在平面直角坐标系中,菱形OABC的顶点O为坐标原点,顶点A在x轴的负半轴上,顶点C反比例函数y=的图象上,若菱形OABC的周长为24,∠B=60°,则k的值为
.
15、如图,在平面直角坐标系中,点A、B在反比例函数y=(x>0)的图象上运动,且始终保持线段AB=4的长度不变,M为线段AB的中点,连接OM,则OM的长度的最小值是
(用含k的代数式表示).
16、如图,A、B两点在反比例函数y=的图象上,C、D两点在反比例函数y=的图象上,CA⊥x轴于E,DB
⊥x轴于F,AC=3,BD
=6,EF=4.则k2k1=
.
17、如图双曲线y=经过点P(2,3),且与直线y=mx5(m<0)有两个不同的交点,
(1)求a的值;(2)求m的取值范围.
?
18、如图,在平面直角坐标系xOy中,已知正比例函数y1=4x的图象与反比例函数y2=的图象交于A(2,m),B两点.
(1)求出反比例函数的解析式及点B的坐标;
(2)观察图象,请直接写出满足y≤8的取值范围;
(3)点C是第四象限内反比例函数的图象上一点,
若△BOC的面积为4,请直接写出点C的
横坐标.
【中考链接】
19、(2019?济南)函数y=ax+a与y=(a≠0)在同一坐标系中的图象可能是( )
20、(2019?台湾)小涵与阿嘉一起去咖啡店购买同种咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结账金额再减5元.若小涵购买咖啡豆250公克且自备容器需支付295元;阿嘉购买咖啡豆x公克没有自备容器,需支付y元,则y与x的关系式为下列何者?
A.
y=
B.
y=
C.y=
D.y=+1
21、(2019?安徽)
已知点A(1,3)关于x轴的对称点在反比例函数的图像上,则实数k的值为(
)
A.3
B.
C.3
D.
22、(2019?枣庄)如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴,y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=1,则k的值为(
)
A.1
B.
C.
D.2
23、(2019?随州)如图,矩形OABC的顶点A、C分别在y轴、x轴的正半轴上,D为AB的中点,反比例函数y=(k>0)的图象经过点D,且与BC交于点E,连接OD、OE、DE,若△ODE的面积为3,则k的值为
.
参考答案
1、D
2、D
3、C
4、B
5、2,
二四
6、0
10、C
11、B
12、A
13、C
14、
15、
16、8
19、D
20、B
21、A
22、A
23、4
7、已知反比例函数y=(k≠0)的图象的一个分支如图所示,请画出它的另一个分支.
8、如图,已知点P是反比例函数y=(k≠0)的图象上任意一点,双曲线y=与双曲线y=
的图象关于y轴对称,过点P作PA⊥x轴,垂足为A,过点P作PB⊥y轴,垂足为B,
求(1)反比例函数的解析式:(2)四边形OAPB的面积.
解:(1)
∵双曲线y=与双曲线y=
的图象关于y轴对称,
∴k=3,
反比例函数的解析式为:y=;
(2)∵点P作PA⊥x轴,点P作PB⊥y轴,∠AOB=90°,
∴四边形OAPB为矩形,
设点P的坐标为(x,y)
矩形OAPB的面积为=3.
9、已知一次函数y=3x2k的图像与反比例函数y=的图像相交,其中有一个交点的纵坐标为2,求(1)这两个函数的解解析式;(2)交点坐标.
解:(1)∵其中一个交点的纵坐标为2,
∴将y
=
2分别代入两个函数中可得:
,
解这个方程组得,
所以一次函数为答?y
=
3x+4,反比例函数为y=;
(2)解方程组得,.
∴一次函数与反比例函数相交点坐标为(2,2)和(,6).
17、如图双曲线y=经过点P(2,3),且与直线y=mx5(m<0)有两个不同的交点,
(1)求a的值;(2)求m的取值范围.
解:(1)∵双曲线y=经过点P(2,3),
∴a=xy=2×3=6;
(2)∵双曲线y=与直线y=mx5(m<0)有两个不同的交点,
∴=
mx5,整理得mx25x6=0,
∴△=(5)24×(6)m>0,
解得m>,
∴m的取值范围是?
18、如图,在平面直角坐标系xOy中,已知正比例函数y1=4x的图象与反比例函数y2=的图象交于A(2,m),B两点.
(1)求出反比例函数的解析式及点B的坐标;
(2)观察图象,请直接写出满足y≤8的取值范围;
(3)点C是第四象限内反比例函数的图象上一点,若△BOC的面积为4,请直接写出点C的
横坐标.
解:(1)把A(2,m)代入y=4x,可得n=8,
∴A(2,8),
把A(2,8)代入y=,可得k=16,
∴反比例函数的表达式为y=,
∵点B与点A关于原点对称,
∴B(2,8).
(2)∵A(2,8),
∴y≤2的取值范围是x<2或x>0;
(3)作BD⊥x轴于D,CE⊥x轴于E,
∵S梯形DBCE=S△BOC=1,
设C(m,),则(8+)(m2)=4或(8+)(2m)=4
整理得,m2m4=0或m2+m4=0,
解得m=或m=,
∴C点的横坐标为或.
第12题图
第23题图
第22题图
第8题图
第7题图
第8题图
第15题图
第7题图
第18题图
第18题图
第16题图
第14题图
第18题图
第7题图
A
B
C
D
①
②
③
④
第13题图
例题2图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.2
反比例函数的图象和性质
第1课时
反比例函数的图象和性质(1)
【知识清单】
1.反比例函数(k≠0)的图象是由两个分支组成的曲线.当k>0时,图象在一、三象限;当k<0时,图象在二、四象限.
2.反比例函数(k≠0)的图象关于直角坐标系的原点成中心对称.
【经典例题】
例题1、若反比例函数的图象位于第二、四象限内,则m的取值范围是( )
A.m>0
B.m<5
C.m>5
D.m<12
【考点】反比例函数的图象和性质.
【分析】根据反比例函数性质:图象位于第二、四象限内,则有k<0,即153m<0,解出m即可.
【解答】根据题意,得153m<0,
解得m>5.
故选C.
【点评】本题主要目的是检查学生对于考点“反比例函数的性质”相关知识的理解.熟练掌握反比例函数的性质是解决问题的关键.
例题2、如图是反比例函数(k>0)的图象在第一象限的部分曲线,P为曲线上任意一点,PM垂直x轴于点M,求△OPM的面积(用用含k的代数式表示).
【考点】反比例函数的图象和性质.
【分析】?设出点P的坐标(x,y),则有△OPM的面积等于点P的纵横坐标的绝对值的积的一半,然后把相关数据代入即可.
【解答】设点P的坐标为(x,y).
∵P(x,y)在第一象限,且在反比例函数(k>0)的图象上,
∴6k=xy,
∴△OPM的面积=xy=×6k=3k.
【点评】本题考查了反比例函数中的k的意义,用到的知识点为,在反比例函数图象的点坐标的绝对值的积等于反比例函数系数的绝对值.
【夯实基础】
1、下列图形中阴影部分面积相等的是(
)
A.①②
B.②③
C.①④
D.③④
2、下列各点中,在反比例函数y=图象上的是(
)
A.
B.
C.
D.
3、反比例函数y=、y=、y=的共同点是(
)
A.图象位于同样的象限
B.自变量的取值范围是任意实数
C.图象关于直角坐标系的原点成中心对称
D.图象可以与坐标轴相交
4、若反比例函数y=的图象在一、三象限,则函数y=axb的图象一定经过的象限为(
)
A.一、三象限
B.二、三象限
C.一、四象限
D.三、四象限
5、若反比例函数y=(m≤5)的图象在一、三象限,则m的取值范围是
.若一次函数y=ax+b的图象不经过第三象限,则反比例函数y=的图象
象限.
6、在平面直角坐标系xOy中,点A(a<0,b<0)在反比例函数y=图象上.点A关于y轴的对称点B在双曲线y=上,则m+n的值为
.
7、已知反比例函数y=(k≠0)的图象的一个分支如图所示,请画出它的另一个分支.
8、如图,已知点P是反比例函数y=(k≠0)的图象上任意一点,双曲线y=与双曲线y=
的图象关于y轴对称,过点P作PA⊥x轴,
垂足为A,过点P作PB⊥y轴,
垂足为B,
求(1)反比例函数的解析式:
(2)四边形OAPB的面积.
9、已知一次函数y=3x2k的图像与反比例函数y=的图像相交,其中有一个交点的纵坐标为2,求(1)这两个函数的解解析式;(2)交点坐标.
【提优特训】
10、在平面直角坐标系xOy中,点P到x轴的距离为5,到原点的距离为13,则经过点P的反比例函数解析式为( )
A.y=
B.y=
C.y=或
y=
D.y=或
y=
11、已知点A是直线y=3x与双曲线y=(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,若OB=4,则m的值(
)
A.12
B.9
C.
8
D.6
12、如图,函数y=的图象所在的坐标原点是
( )
A.?M?????
???B.N?????????
?C.?Q?????
??D.P
13、如图,在平面直角坐标系xOy中,点A、B、C为反比例函数y=(k>0)的图象上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作x轴的垂线,垂足分别为E、F,OC与BE相交于点P,记△OAD,△OBP,四边形CPEF的面积分别为S1、S2、S3,则
( )
A.?S1=S2+S3????????
?B.S1>S3>S2????????
?
C.S1>?S2=S3????
???D.S1S2=S32
14、如图,在平面直角坐标系中,菱形OABC的顶点O为坐标原点,顶点A在x轴的负半轴上,顶点C反比例函数y=的图象上,若菱形OABC的周长为24,∠B=60°,则k的值为
.
15、如图,在平面直角坐标系中,点A、B在反比例函数y=(x>0)的图象上运动,且始终保持线段AB=4的长度不变,M为线段AB的中点,连接OM,则OM的长度的最小值是
(用含k的代数式表示).
16、如图,A、B两点在反比例函数y=的图象上,C、D两点在反比例函数y=的图象上,CA⊥x轴于E,DB
⊥x轴于F,AC=3,BD
=6,EF=4.则k2k1=
.
17、如图双曲线y=经过点P(2,3),且与直线y=mx5(m<0)有两个不同的交点,
(1)求a的值;(2)求m的取值范围.
?
18、如图,在平面直角坐标系xOy中,已知正比例函数y1=4x的图象与反比例函数y2=的图象交于A(2,m),B两点.
(1)求出反比例函数的解析式及点B的坐标;
(2)观察图象,请直接写出满足y≤8的取值范围;
(3)点C是第四象限内反比例函数的图象上一点,
若△BOC的面积为4,请直接写出点C的
横坐标.
【中考链接】
19、(2019?济南)函数y=ax+a与y=(a≠0)在同一坐标系中的图象可能是( )
20、(2019?台湾)小涵与阿嘉一起去咖啡店购买同种咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结账金额再减5元.若小涵购买咖啡豆250公克且自备容器需支付295元;阿嘉购买咖啡豆x公克没有自备容器,需支付y元,则y与x的关系式为下列何者?
A.
y=
B.
y=
C.y=
D.y=+1
21、(2019?安徽)
已知点A(1,3)关于x轴的对称点在反比例函数的图像上,则实数k的值为(
)
A.3
B.
C.3
D.
22、(2019?枣庄)如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴,y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=1,则k的值为(
)
A.1
B.
C.
D.2
23、(2019?随州)如图,矩形OABC的顶点A、C分别在y轴、x轴的正半轴上,D为AB的中点,反比例函数y=(k>0)的图象经过点D,且与BC交于点E,连接OD、OE、DE,若△ODE的面积为3,则k的值为
.
参考答案
1、D
2、D
3、C
4、B
5、2
二四
6、0
10、C
11、B
12、A
13、C
14、
15、
16、8
19、D
20、B
21、A
22、A
23、4
7、已知反比例函数y=(k≠0)的图象的一个分支如图所示,请画出它的另一个分支.
8、如图,已知点P是反比例函数y=(k≠0)的图象上任意一点,双曲线y=与双曲线y=
的图象关于y轴对称,过点P作PA⊥x轴,垂足为A,过点P作PB⊥y轴,垂足为B,
求(1)反比例函数的解析式:(2)四边形OAPB的面积.
解:(1)
∵双曲线y=与双曲线y=
的图象关于y轴对称,
∴k=3,
反比例函数的解析式为:y=;
(2)∵点P作PA⊥x轴,点P作PB⊥y轴,∠AOB=90°,
∴四边形OAPB为矩形,
设点P的坐标为(x,y)
矩形OAPB的面积为=3.
9、已知一次函数y=3x2k的图像与反比例函数y=的图像相交,其中有一个交点的纵坐标为2,求(1)这两个函数的解解析式;(2)交点坐标.
解:(1)∵其中一个交点的纵坐标为2,
∴将y
=
2分别代入两个函数中可得:
,
解这个方程组得,
所以一次函数为答?y
=
3x+4,反比例函数为y=;
(2)解方程组得,.
∴一次函数与反比例函数相交点坐标为(2,2)和(,6).
17、如图双曲线y=经过点P(2,3),且与直线y=mx5(m<0)有两个不同的交点,
(1)求a的值;(2)求m的取值范围.
解:(1)∵双曲线y=经过点P(2,3),
∴a=xy=2×3=6;
(2)∵双曲线y=与直线y=mx5(m<0)有两个不同的交点,
∴=
mx5,整理得mx25x6=0,
∴△=(5)24×(6)m>0,
解得m>,
∴m的取值范围是
18、如图,在平面直角坐标系xOy中,已知正比例函数y1=4x的图象与反比例函数y2=的图象交于A(2,m),B两点.
(1)求出反比例函数的解析式及点B的坐标;
(2)观察图象,请直接写出满足y≤8的取值范围;
(3)点C是第四象限内反比例函数的图象上一点,若△BOC的面积为4,请直接写出点C的
横坐标.
解:(1)把A(2,m)代入y=4x,可得n=8,
∴A(2,8),
把A(2,8)代入y=,可得k=16,
∴反比例函数的表达式为y=,
∵点B与点A关于原点对称,
∴B(2,8).
(2)∵A(2,8),
∴y≤2的取值范围是x<2或x>0;
(3)作BD⊥x轴于D,CE⊥x轴于E,
∵S梯形DBCE=S△BOC=1,
设C(m,),则(8+)(m2)=4或(8+)(2m)=4
整理得,m2m4=0或m2+m4=0,
解得m=或m=,
∴C点的横坐标为或.
第12题图
第23题图
第22题图
第8题图
第7题图
第8题图
第15题图
第7题图
第18题图
第18题图
第16题图
第14题图
第18题图
第7题图
A
B
C
D
①
②
③
④
第13题图
例题2图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
