第四章 平行四边形单元基础测试卷(解析版+学生卷)
文档属性
| 名称 | 第四章 平行四边形单元基础测试卷(解析版+学生卷) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 10:28:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【单元双测卷——基础测】
第四章
平行四边形
说明:全卷满分120分,有三大题,共24小题.
班级:__________
姓名:__________
得分:__________
一、选择题(本题有10小题,每题3分,共30分.
请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下面四个图案依次是我国汉字中的“福禄寿喜”的艺术字图.这四个图案中是中心对称图形的是(
)
A.①②
B.②③
C.②④
D.②③④
2.下面给出的四边形ABCD中,∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的条件是(
)
A.3∶4∶3∶4
B.3∶3∶4∶4
C.2∶3∶4∶5
D.3∶4∶4∶3
3.如图,、分别是平行四边形的边、所在直线上的点,、交于点,请你添加一个条件,使四边形是平行四边形,下列选项中不能推断四边形是平行四边形的是(
)
A.
B.
C.
D.
第3题图
第5题图
4.若以A(﹣1,0),B(3,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.如图,?ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为(
)
A.15
B.18
C.21
D.24
6.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
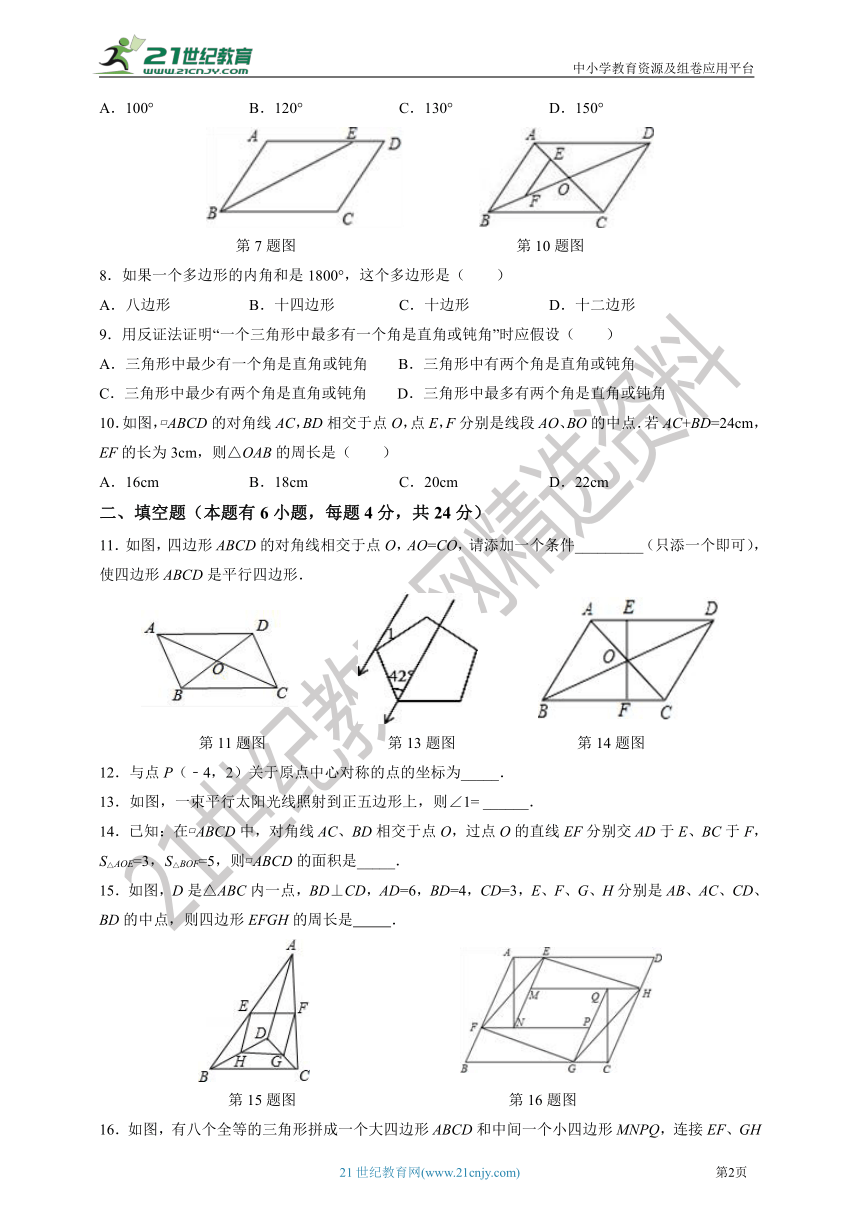
7.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为(
)
A.100°
B.120°
C.130°
D.150°
第7题图
第10题图
8.如果一个多边形的内角和是1800°,这个多边形是(
)
A.八边形
B.十四边形
C.十边形
D.十二边形
9.用反证法证明“一个三角形中最多有一个角是直角或钝角”时应假设(
)
A.三角形中最少有一个角是直角或钝角
B.三角形中有两个角是直角或钝角
C.三角形中最少有两个角是直角或钝角
D.三角形中最多有两个角是直角或钝角
10.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是(
)
A.16cm
B.18cm
C.20cm
D.22cm
二、填空题(本题有6小题,每题4分,共24分)
11.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________(只添一个即可),使四边形ABCD是平行四边形.
第11题图
第13题图
第14题图
12.与点P(﹣4,2)关于原点中心对称的点的坐标为_____.
13.如图,一束平行太阳光线照射到正五边形上,则∠1=
______.
14.已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是_____.
15.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是
.
第15题图
第16题图
16.如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设
,
,
,若S1+S2+S3=10,则S2=______.
三、解答题(本题有8小题,共66分.解答应写出文字说明、证明过程或演算步骤)
17.(本题6分)一个多边形的内角和是它的外角和的3倍,求这个多边形的边数。
18.(本题6分)如图,方格纸上每个小正方形的边长均为个单位长度,点都在格点上(两条网格线的交点叫格点).
将线段平移到,使得点和点关于原点对称,请画出平移后的线段;
在坐标系中找出一个格点(任找一个即可),使得标出点坐标,并直接写出此时
.
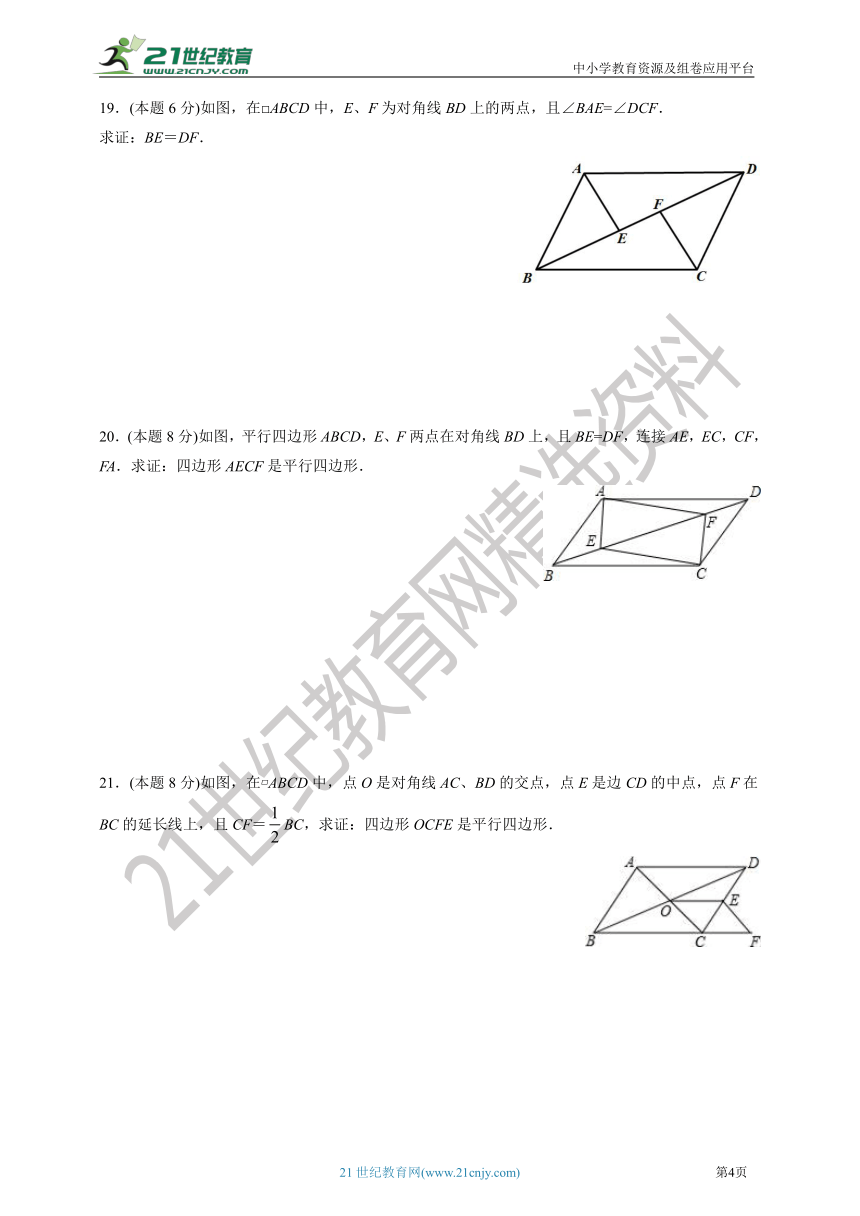
19.(本题6分)如图,在□ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.
求证:BE=DF.
20.(本题8分)如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
21.(本题8分)如图,在?ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.
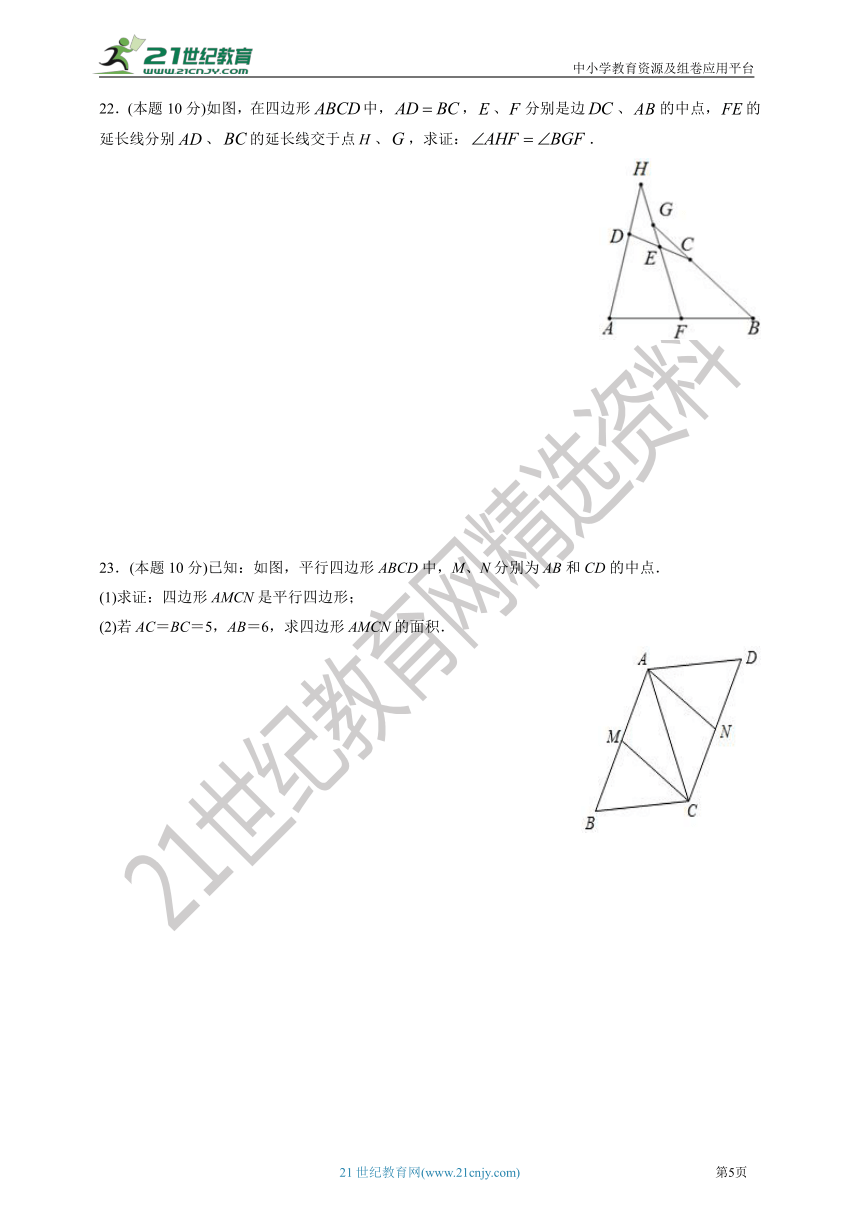
22.(本题10分)如图,在四边形中,,、分别是边、的中点,的延长线分别、的延长线交于点、,求证:.
23.(本题10分)已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCN的面积.
24.(本题12分)如图,四边形是平行四边形,,,点是的中点,点是延长线上一点.
(1)若,求证:.
(2)在(1)的条件下,若的延长线与交于点,试判断四边形是否为平行四边形,并证明你的结论(请补全图形,再解答)
(3)若,与垂直吗?若垂直,请给予证明.
答案及解析
1.C
【解析】根据中心对称图形的概念可知第②和第④个图形为中心对称图形,故选C.
2.A
【解析】由于平行四边形的两组对角分别相等,故只有D能判定是平行四边形.其它三个选项不能满足两组对角相等,故不能判定.
解:根据平行四边形的两组对角分别相等,可知A正确,B,C,D错误
故选:A.
3.A
【解析】根据平行四边形的性质得出AF∥CE,再根据平行四边形的判定定理得出即可.
解:∵四边形是平行四边形,
∴,,即.
A、时,一组对边平行,另一组对边相等不能判定四边形为平行四边形,故错误;
B、,又∵,∴四边形为平行四边形;
C、∵,,∴四边形是平行四边形;
D、∵,,∴四边形是平行四边形.
故选:A.
4.C
【解析】首先画出平面直角坐标系,根据A、B、C三点的坐标找出其位置,然后再根据两组对边分别平行的四边形是平行四边形找出D的位置,进而可得答案.
解:如图所示:
第四个顶点不可能在第三象限.
故选C.
5.A
【解析】此题涉及的知识点是平行四边形的性质.根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
解:∵?ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,DE=CD,
∴OE是△BCD的中位线,∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故选A
6.C
【解析】由题意得,180°(n-2)=120°,
解得n=6.故选C.
7.C
【解析】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠CBE.
∵∠ABC的平分线交AD于E,∴∠ABE=∠CBE=∠AEB=25°,∴∠A=180°-∠ABE-∠AEB=130°.故选C.
8.D
【解析】n边形的内角和可以表示成(n﹣2)?180°,设这个正多边形的边数是n,就得到方程,从而求出边数.
解:这个正多边形的边数是n,根据题意得:
(n﹣2)?180°=1800°
解得:n=12.
故选D.
9.C
【解析】利用反证法证明一个命题,首先要假设所证的结论不正确,结论的反面正确.
解:假设正确的是:假设三角形中最少有两个角是直角或钝角.
故选:C.
10.B
【解析】∵?ABCD的对角线AC,BD相交于点O,
∴OA=AC,OB=BD,
∵AC+BD=24cm,
∴OB+0A=12cm,
∵点E,F分别是线段AO,BO的中点,
∴AB=2EF=6cm,
∴△OAB的周长=OA+OB+AB=12+6=18(cm);
故选B.
11.BO=DO.
【解析】解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
故答案为BO=DO.
12.(4,﹣2).
【解析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y).据此作答.
解:根据中心对称的性质,得点P(﹣4,2)关于原点中心对称的点的坐标为(4,﹣2).
故答案为:(4,﹣2).
13.30°.
【解析】解:∵AB//CD,∴∠BAC+∠ACD=180°,即∠1+∠EAC+∠ACD=180°,
∵五边形是正五边形,∴∠EAC=108°,
∵∠ACD=42°,∴∠1=180°-42°-108°=30°
故答案为:30°.
14.32
【解析】解:分析:利用平行四边形的性质可证明△AOF≌△COE,所以可得△COE的面积为3,进而可得△BOC的面积为8,又因为△BOC的面积=?ABCD的面积,进而可得问题答案.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠BCA,∠AEF=∠CFE,
又∵AO=CO,
在△AOE与△COF中
∴△AOE≌△COF
∴△COEF的面积为3,
∵S△BOF=5,
∴△BOC的面积为8,
∵△BOC的面积=?ABCD的面积,
∴?ABCD的面积=4×8=32,
故答案为32.
15.11.
【解析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解:
∵BD⊥CD,BD=4,CD=3,∴.
∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=AD,EF=GH=BC.
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC.
又∵AD=6,∴四边形EFGH的周长=6+5=11.
16.
【解析】根据图形的特征,将四边形MNPQ的面积设为x,将其余八个全等的三角形面积一个设为y,由S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,可得出S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=10,即3x+12y=10,化简为x+4y=,因此可得S2=x+4y=.
故答案为.
17.这个多边形的边数是8.
【解析】根据多边形的外角和为360°,内角和公式为:(n-2)?180°,由题意可知:内角和=3×外角和,设出未知数,可得到方程,解方程即可.
解:设这个多边形是n边形,
由题意得:(n-2)×180°=360°×3,
解得:n=8.
答:这个多边形的边数是8.
18.(1)见解析;(2)见解析,.
【解析】(1)根据点和点关于原点对称可得的位置,进而得出的位置即可;
(2)根据网格特点可得点位置,根据三角形面积公式可得.
解:(1)如图,线段即为所求;
(2)如图,点C(-5,0)即为所求,.
19.见解析
【解析】证明:∵
□ABCD
∴AB∥CD
∵AB∥CD
∴∠ABD=∠CDF
在△ABE与△CDF中
∴△ABD≌△CDF(ASA)
∴BE=DF
20.证明见解析.
【解析】根据两条对角线相互平分的四边形是平行四边形即可证明四边形AECF是平行四边形.
证明:
连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF为平行四边形.
21.证明见解析.
【解析】利用三角形中位线定理判定OE∥BC,且OE=BC.结合已知条件CF=BC,则OE//CF,由“有一组对边平行且相等的四边形为平行四边形”证得结论.
证明:∵四边形ABCD是平行四边形,∴点O是BD的中点.
又∵点E是边CD的中点,∴OE是△BCD的中位线,∴OE∥BC,且OE=BC.
又∵CF=BC,∴OE=CF.
又∵点F在BC的延长线上,∴OE∥CF,
∴四边形OCFE是平行四边形.
22.证明见解析
【解析】连接BD,取BD的中点,连接EP,FP,根据三角形中位线定理即可得到PF=AD,PF∥AD,EP=BC,EP∥BC,进而得出∠AHF=∠BGF.
证明:如图所示,连接BD,取BD的中点,连接EP,FP,
∵E、F分别是DC、AB边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
又∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
23.(1)见解析;(2)12.
【解析】(1)由题意可得AB∥CD,AB=CD,又由M,N分别是AB和CD的中点可得AM=∥CN,即可得结论;
(2)根据等腰三角形的性质可得CM⊥AB,AM=3,根据勾股定理可得CM=4,则可求面积.
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵M,N分别为AB和CD的中点,
∴AM=AB,CN=CD,
∴AM=CN,且AB∥CD,
∴四边形AMCN是平行四边形;
(2)∵AC=BC=5,AB=6,M是AB中点,
∴AM=MB=3,CM⊥AM,
∴CM=,
∵四边形AMCN是平行四边形,且CM⊥SM,
∴AMCN是矩形,
∴S四边形AMCN=12.
24.答案见解析.
【解析】(1)根据平行四边形的想知道的AD=AC,AD⊥AC,连接CE,根据全等三角形的判定和性质即可得到结论;
(2)根据全等三角形的性质得到CF=AD,等量代换得到AC=CF,于是得到CP=AB=AE,根据平行四边形的判定定理即可得到四边形ACPE为平行四边形;
(3)过E作EM⊥DA交DA的延长线于M,过E作EN⊥FC交FC的延长线于N,证得△AME≌△CNE,△ADE≌△CFE,根据全等三角形的性质即可得到结论.
证明:(1)在?ABCD中,∵AD=AC,AD⊥AC,∴AC=BC,AC⊥BC,连接CE,
∵E是AB的中点,∴AE=EC,CE⊥AB,∴∠ACE=∠BCE=45°,∴∠ECF=∠EAD=135°,
∵ED⊥EF,∴∠CEF=∠AED=90°﹣∠CED,
在△CEF和△AED中,∵∠CEF=∠AED,EC=AE,∠ECF=∠EAD,∴△CEF≌△AED,
∴ED=EF;
(2)由(1)知△CEF≌△AED,CF=AD,∵AD=AC,∴AC=CF,
∵DP∥AB,∴FP=PB,∴CP=AB=AE,∴四边形ACPE为平行四边形;
(3)垂直,理由:过E作EM⊥DA交DA的延长线于M,过E作EN⊥FC交FC的延长线于N,在△AME与△CNE中,∵∠M=∠FNE=90°,∠EAM=∠NCE=45°,AE=CE,
∴△AME≌△CNE,∴∠ADE=∠CFE,
在△ADE与△CFE中,∵∠ADE=∠CFE,∠DAE=∠FCE=135°,DE=EF,
∴△ADE≌△CFE,∴∠DEA=∠FEC,
∵∠DEA+∠DEC=90°,∴∠CEF+∠DEC=90°,∴∠DEF=90°,∴ED⊥EF.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第14页
【单元双测卷——基础测】
第四章
平行四边形
说明:全卷满分120分,有三大题,共24小题.
班级:__________
姓名:__________
得分:__________
一、选择题(本题有10小题,每题3分,共30分.
请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下面四个图案依次是我国汉字中的“福禄寿喜”的艺术字图.这四个图案中是中心对称图形的是(
)
A.①②
B.②③
C.②④
D.②③④
2.下面给出的四边形ABCD中,∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的条件是(
)
A.3∶4∶3∶4
B.3∶3∶4∶4
C.2∶3∶4∶5
D.3∶4∶4∶3
3.如图,、分别是平行四边形的边、所在直线上的点,、交于点,请你添加一个条件,使四边形是平行四边形,下列选项中不能推断四边形是平行四边形的是(
)
A.
B.
C.
D.
第3题图
第5题图
4.若以A(﹣1,0),B(3,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.如图,?ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为(
)
A.15
B.18
C.21
D.24
6.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
7.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为(
)
A.100°
B.120°
C.130°
D.150°
第7题图
第10题图
8.如果一个多边形的内角和是1800°,这个多边形是(
)
A.八边形
B.十四边形
C.十边形
D.十二边形
9.用反证法证明“一个三角形中最多有一个角是直角或钝角”时应假设(
)
A.三角形中最少有一个角是直角或钝角
B.三角形中有两个角是直角或钝角
C.三角形中最少有两个角是直角或钝角
D.三角形中最多有两个角是直角或钝角
10.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是(
)
A.16cm
B.18cm
C.20cm
D.22cm
二、填空题(本题有6小题,每题4分,共24分)
11.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________(只添一个即可),使四边形ABCD是平行四边形.
第11题图
第13题图
第14题图
12.与点P(﹣4,2)关于原点中心对称的点的坐标为_____.
13.如图,一束平行太阳光线照射到正五边形上,则∠1=
______.
14.已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是_____.
15.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是
.
第15题图
第16题图
16.如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设
,
,
,若S1+S2+S3=10,则S2=______.
三、解答题(本题有8小题,共66分.解答应写出文字说明、证明过程或演算步骤)
17.(本题6分)一个多边形的内角和是它的外角和的3倍,求这个多边形的边数。
18.(本题6分)如图,方格纸上每个小正方形的边长均为个单位长度,点都在格点上(两条网格线的交点叫格点).
将线段平移到,使得点和点关于原点对称,请画出平移后的线段;
在坐标系中找出一个格点(任找一个即可),使得标出点坐标,并直接写出此时
.
19.(本题6分)如图,在□ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.
求证:BE=DF.
20.(本题8分)如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
21.(本题8分)如图,在?ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.
22.(本题10分)如图,在四边形中,,、分别是边、的中点,的延长线分别、的延长线交于点、,求证:.
23.(本题10分)已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCN的面积.
24.(本题12分)如图,四边形是平行四边形,,,点是的中点,点是延长线上一点.
(1)若,求证:.
(2)在(1)的条件下,若的延长线与交于点,试判断四边形是否为平行四边形,并证明你的结论(请补全图形,再解答)
(3)若,与垂直吗?若垂直,请给予证明.
答案及解析
1.C
【解析】根据中心对称图形的概念可知第②和第④个图形为中心对称图形,故选C.
2.A
【解析】由于平行四边形的两组对角分别相等,故只有D能判定是平行四边形.其它三个选项不能满足两组对角相等,故不能判定.
解:根据平行四边形的两组对角分别相等,可知A正确,B,C,D错误
故选:A.
3.A
【解析】根据平行四边形的性质得出AF∥CE,再根据平行四边形的判定定理得出即可.
解:∵四边形是平行四边形,
∴,,即.
A、时,一组对边平行,另一组对边相等不能判定四边形为平行四边形,故错误;
B、,又∵,∴四边形为平行四边形;
C、∵,,∴四边形是平行四边形;
D、∵,,∴四边形是平行四边形.
故选:A.
4.C
【解析】首先画出平面直角坐标系,根据A、B、C三点的坐标找出其位置,然后再根据两组对边分别平行的四边形是平行四边形找出D的位置,进而可得答案.
解:如图所示:
第四个顶点不可能在第三象限.
故选C.
5.A
【解析】此题涉及的知识点是平行四边形的性质.根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
解:∵?ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,DE=CD,
∴OE是△BCD的中位线,∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故选A
6.C
【解析】由题意得,180°(n-2)=120°,
解得n=6.故选C.
7.C
【解析】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠CBE.
∵∠ABC的平分线交AD于E,∴∠ABE=∠CBE=∠AEB=25°,∴∠A=180°-∠ABE-∠AEB=130°.故选C.
8.D
【解析】n边形的内角和可以表示成(n﹣2)?180°,设这个正多边形的边数是n,就得到方程,从而求出边数.
解:这个正多边形的边数是n,根据题意得:
(n﹣2)?180°=1800°
解得:n=12.
故选D.
9.C
【解析】利用反证法证明一个命题,首先要假设所证的结论不正确,结论的反面正确.
解:假设正确的是:假设三角形中最少有两个角是直角或钝角.
故选:C.
10.B
【解析】∵?ABCD的对角线AC,BD相交于点O,
∴OA=AC,OB=BD,
∵AC+BD=24cm,
∴OB+0A=12cm,
∵点E,F分别是线段AO,BO的中点,
∴AB=2EF=6cm,
∴△OAB的周长=OA+OB+AB=12+6=18(cm);
故选B.
11.BO=DO.
【解析】解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
故答案为BO=DO.
12.(4,﹣2).
【解析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y).据此作答.
解:根据中心对称的性质,得点P(﹣4,2)关于原点中心对称的点的坐标为(4,﹣2).
故答案为:(4,﹣2).
13.30°.
【解析】解:∵AB//CD,∴∠BAC+∠ACD=180°,即∠1+∠EAC+∠ACD=180°,
∵五边形是正五边形,∴∠EAC=108°,
∵∠ACD=42°,∴∠1=180°-42°-108°=30°
故答案为:30°.
14.32
【解析】解:分析:利用平行四边形的性质可证明△AOF≌△COE,所以可得△COE的面积为3,进而可得△BOC的面积为8,又因为△BOC的面积=?ABCD的面积,进而可得问题答案.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠BCA,∠AEF=∠CFE,
又∵AO=CO,
在△AOE与△COF中
∴△AOE≌△COF
∴△COEF的面积为3,
∵S△BOF=5,
∴△BOC的面积为8,
∵△BOC的面积=?ABCD的面积,
∴?ABCD的面积=4×8=32,
故答案为32.
15.11.
【解析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解:
∵BD⊥CD,BD=4,CD=3,∴.
∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=AD,EF=GH=BC.
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC.
又∵AD=6,∴四边形EFGH的周长=6+5=11.
16.
【解析】根据图形的特征,将四边形MNPQ的面积设为x,将其余八个全等的三角形面积一个设为y,由S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,可得出S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=10,即3x+12y=10,化简为x+4y=,因此可得S2=x+4y=.
故答案为.
17.这个多边形的边数是8.
【解析】根据多边形的外角和为360°,内角和公式为:(n-2)?180°,由题意可知:内角和=3×外角和,设出未知数,可得到方程,解方程即可.
解:设这个多边形是n边形,
由题意得:(n-2)×180°=360°×3,
解得:n=8.
答:这个多边形的边数是8.
18.(1)见解析;(2)见解析,.
【解析】(1)根据点和点关于原点对称可得的位置,进而得出的位置即可;
(2)根据网格特点可得点位置,根据三角形面积公式可得.
解:(1)如图,线段即为所求;
(2)如图,点C(-5,0)即为所求,.
19.见解析
【解析】证明:∵
□ABCD
∴AB∥CD
∵AB∥CD
∴∠ABD=∠CDF
在△ABE与△CDF中
∴△ABD≌△CDF(ASA)
∴BE=DF
20.证明见解析.
【解析】根据两条对角线相互平分的四边形是平行四边形即可证明四边形AECF是平行四边形.
证明:
连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF为平行四边形.
21.证明见解析.
【解析】利用三角形中位线定理判定OE∥BC,且OE=BC.结合已知条件CF=BC,则OE//CF,由“有一组对边平行且相等的四边形为平行四边形”证得结论.
证明:∵四边形ABCD是平行四边形,∴点O是BD的中点.
又∵点E是边CD的中点,∴OE是△BCD的中位线,∴OE∥BC,且OE=BC.
又∵CF=BC,∴OE=CF.
又∵点F在BC的延长线上,∴OE∥CF,
∴四边形OCFE是平行四边形.
22.证明见解析
【解析】连接BD,取BD的中点,连接EP,FP,根据三角形中位线定理即可得到PF=AD,PF∥AD,EP=BC,EP∥BC,进而得出∠AHF=∠BGF.
证明:如图所示,连接BD,取BD的中点,连接EP,FP,
∵E、F分别是DC、AB边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
又∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
23.(1)见解析;(2)12.
【解析】(1)由题意可得AB∥CD,AB=CD,又由M,N分别是AB和CD的中点可得AM=∥CN,即可得结论;
(2)根据等腰三角形的性质可得CM⊥AB,AM=3,根据勾股定理可得CM=4,则可求面积.
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵M,N分别为AB和CD的中点,
∴AM=AB,CN=CD,
∴AM=CN,且AB∥CD,
∴四边形AMCN是平行四边形;
(2)∵AC=BC=5,AB=6,M是AB中点,
∴AM=MB=3,CM⊥AM,
∴CM=,
∵四边形AMCN是平行四边形,且CM⊥SM,
∴AMCN是矩形,
∴S四边形AMCN=12.
24.答案见解析.
【解析】(1)根据平行四边形的想知道的AD=AC,AD⊥AC,连接CE,根据全等三角形的判定和性质即可得到结论;
(2)根据全等三角形的性质得到CF=AD,等量代换得到AC=CF,于是得到CP=AB=AE,根据平行四边形的判定定理即可得到四边形ACPE为平行四边形;
(3)过E作EM⊥DA交DA的延长线于M,过E作EN⊥FC交FC的延长线于N,证得△AME≌△CNE,△ADE≌△CFE,根据全等三角形的性质即可得到结论.
证明:(1)在?ABCD中,∵AD=AC,AD⊥AC,∴AC=BC,AC⊥BC,连接CE,
∵E是AB的中点,∴AE=EC,CE⊥AB,∴∠ACE=∠BCE=45°,∴∠ECF=∠EAD=135°,
∵ED⊥EF,∴∠CEF=∠AED=90°﹣∠CED,
在△CEF和△AED中,∵∠CEF=∠AED,EC=AE,∠ECF=∠EAD,∴△CEF≌△AED,
∴ED=EF;
(2)由(1)知△CEF≌△AED,CF=AD,∵AD=AC,∴AC=CF,
∵DP∥AB,∴FP=PB,∴CP=AB=AE,∴四边形ACPE为平行四边形;
(3)垂直,理由:过E作EM⊥DA交DA的延长线于M,过E作EN⊥FC交FC的延长线于N,在△AME与△CNE中,∵∠M=∠FNE=90°,∠EAM=∠NCE=45°,AE=CE,
∴△AME≌△CNE,∴∠ADE=∠CFE,
在△ADE与△CFE中,∵∠ADE=∠CFE,∠DAE=∠FCE=135°,DE=EF,
∴△ADE≌△CFE,∴∠DEA=∠FEC,
∵∠DEA+∠DEC=90°,∴∠CEF+∠DEC=90°,∴∠DEF=90°,∴ED⊥EF.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第14页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
