第四章 平行四边形单元能力测试卷(解析版+学生卷)
文档属性
| 名称 | 第四章 平行四边形单元能力测试卷(解析版+学生卷) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 10:35:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【单元双测卷——能力测】
第四章
平行四边形
说明:全卷满分120分,有三大题,共24小题.
班级:__________
姓名:__________
得分:__________
一、选择题(本题有10小题,每题3分,共30分.
请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下列图形均是一些科技创新公司标志图,其中既是中心对称图形又是轴对称图形的是(
)
A.
B.??
C.?????
D.
2.在下列性质中,平行四边形不一定具有的是(
)
A.对边相等
B.对角互补
C.对边平行
D.对角相等
3.如图,
中,,平分交
边于点,且
,则
的长为(
)
A.3
B.4
C.2
D.5
第3题图
第4题图
第6题图
4.如图,ABCD中,E,F分别是AB,CD的中点,则图中有________个平行四边形.(
)
A.7个
B.8个
C.9个
D.10个
5.把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为(
)
A.9
B.10
C.11
D.以上都有可能
6.如图,平面直角坐标系中,平行四边形ABCD的中心E的坐标为(2,0),若点A的坐标为(-2,1),则点C的坐标为(
)
A.(4,-1)
B.(6,-1)
C.(8,-1)
D.(6,-2)
7.已知四边形ABCD中有四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从中任选两个,不能使四边形ABCD成为平行四边形的是(
)
A.①②
B.①③
C.①④
D.②④
8.如图①,平行四边形纸片ABCD的面积为60,沿对角线AC,BD将其裁剪成四个三角形纸片,将纸片△AOD翻转后,与纸片△COB拼接成如图②所示的四边形(点A与点C,点D与点B重合),则拼接后的四边形的两条对角线之积为(
)
A.30
B.40
C.50
D.60
第8题图
第9题图
第10题图
9.如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为(
)
A.10°
B.15°
C.25°
D.40°
10.如图,已知在?ABCD中,分别以AB,AD为边分别向外作等边三角形ABE和等边三角形ADF,延长CB交AE于点G,点G在点A,E之间,连接CE,CF,EF,则下列结论不一定正确的是(
)
A.△CDF≌△EBC
B.∠CDF=∠EAF
C.△ECF是等边三角形
D.CG⊥AE
二、填空题(本题有6小题,每题4分,共24分)
11.若点A(﹣2,n)在x轴上,则点B(n﹣1,n+1)关于原点对称的点的坐标为_____.
12.如图,∠A+∠B+∠C+∠D+∠E+∠F=__________.
第12题图
第14题图
第16题图
13.用反证法证明“三角形中必有一个内角不小于60°”,应当先假设这个三角形中_________.
14.如图,有一张直角三角形纸片,,,,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是______.
15.一个四边形剪去一三角形后余下的多边形为
___________
边形
16.如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
三、解答题(本题有8小题,共66分.解答应写出文字说明、证明过程或演算步骤)
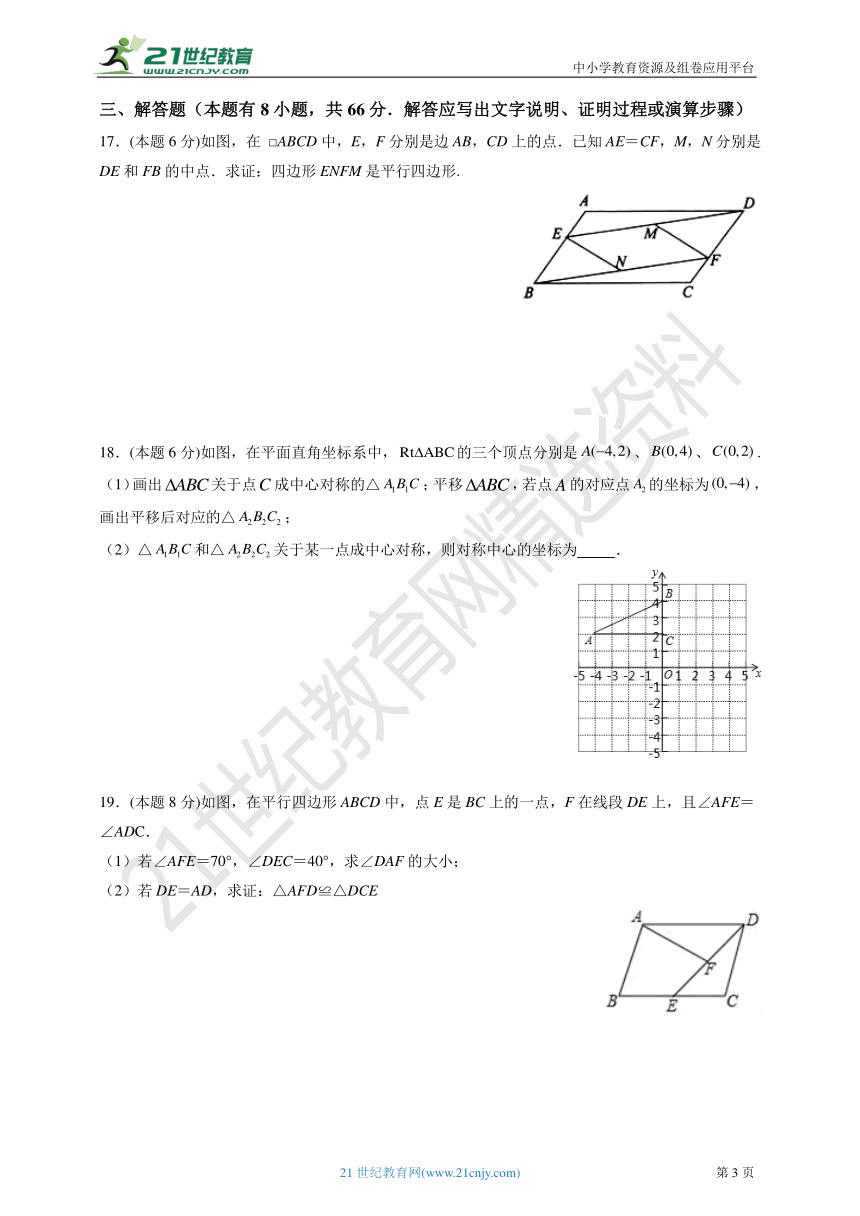
17.(本题6分)如图,在
□ABCD中,E,F分别是边AB,CD上的点.已知AE=CF,M,N分别是DE和FB的中点.求证:四边形ENFM是平行四边形.
18.(本题6分)如图,在平面直角坐标系中,的三个顶点分别是、、.
(1)画出关于点成中心对称的△;平移,若点的对应点的坐标为,画出平移后对应的△;
(2)△和△关于某一点成中心对称,则对称中心的坐标为
.
19.(本题8分)如图,在平行四边形ABCD中,点E是BC上的一点,F在线段DE上,且∠AFE=∠ADC.
(1)若∠AFE=70°,∠DEC=40°,求∠DAF的大小;
(2)若DE=AD,求证:△AFD≌△DCE
20.(本题8分)如图,在平行四边形ABCD中,AB=,BC=8,∠B=60°,将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,折叠后点C的对应点为C′,D′C′交BC于点G,∠BGD′=32°.
(1)求∠D′EF的度数;
(2)求线段AE的长.
21.(本题8分)看图回答问题:
(1)内角和为2014°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?它是多少度?
22.(本题10分)在平行四边形ABCD中,点E是AD边上的点,连接BE.
(1)如图1,若BE平分∠ABC,BC=8,ED=3,求平行四边形ABCD的周长;
(2)如图2,点F是平行四边形外一点,FB=CD.连接BF、CF,CF与BE相交于点G,若∠FBE+∠ABC=180°,点G是CF的中点,求证:2BG+ED=BC.
23.(本题10分)(1)已知:如图1,P为内一点,DP、CP分别平分和,如果,那么________;如果,那么________;如果,则________;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分和,试探究与的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平分和,请直接写出与的数量关系:________________;
(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平分和,请直接写出与的数量关系:________________;
(5)若P为n边形内一点,平分,平分,请直接写出与的数量关系:________________.(用含n的代数式表示)
24.(本题10分)已知在中,动点在边上,以每秒的速度从点向点运动.
(1)如图1,在运动过程中,若平分,且满足,求的度数.
(2)如图2,在(1)的条件下,连结并延长与的延长线交于点,连结,若,求的面积.
(3)如图3,另一动点在边上,以每秒的速度从点出发,在间往返运动,两点同时出发,当点到达点时停止运动(同时点也停止),若,求当运动时间为多少秒时,以D,四点组成的四边形是平行四边形.
答案及解析
1.D
【解析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.
解:A、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误;
B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
C、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.
故选D.
2.B
【解析】根据平行四边形的性质逐项排除即可.
解:∵平行四边形的对边平行、对角相等、对边相等,
∴选项B不正确;
故答案为B.
3.B
【解析】求证DC=DE,再由平行四边形得AD=BC,即可求出AB长.
解:∵四边形ABCD为平行四边形,
∴AD=BC=7,AD∥BC,DC=AB,
∴∠DEC=∠ECB,
∵平分,
∴∠ECB=∠ECD,
∴∠DEC=∠DCE,
∴DE=DC,
∵AE=3,
∴DE=7-3=4,
∴AB=CD=DE=4,
故选B.
4.B
【解析】根据平行四边的判定及中位线定理,利用三角形全等,可推出8个平行四边形.
解:E,F分别是AD,BC的中点,则有,
∴四边形AECF,EDFB,是平行四边形,有∠FBE=∠EDF=∠AEB,
∵AE∥BF
∴EAF=∠AFB
∴根据ASA得出△MAE≌△MFB,∴AM=MF,即点M是AF的中点,
同理,点N是FD的中点,∴MN是△EBC和△AFD的中位线,∴,
∴四边形AENM,DEMN,BMNF,FCNM是平行四边形
∵EN∥MF,ME∥FN
∴四边形ENFM是平行四边形,而四边形ABCD也是平行四边形,共8个平行四边形.
故选B.
5.D
【解析】设新多边形的边数为n,则由题意可得:180(n-2)=1440,解得:n=10,
∵多边形截去一个角之后,新多边形的边数可能和原多边形相同,可能比原多边形多一边,也可能比原多边形少一边,
∴原多边形的边数可能是9或10或11.
故选D.
6.B
【解析】首先连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,E是平行四边形ABCD的中心,即可得AC过点E,易证得△AEG≌△CEH,继而求得答案.
解:连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,
∵E是平行四边形ABCD的中心,
∴AC过点E,
∴AE=CE,
在△AEG和△CEH中,
,
∴△AEG≌△CEH(AAS),
∴EG=EH,CH=AG,
∵E的坐标为(2,0),点A的坐标为(-2,1),
∴EH=EG=4,CH=AG=1,
∴OH=OE+EH=6,
∴点C的坐标为:(6,-1).
故选B.
7.C
【解析】根据平行四边形的判定可直接判断.
解:A、①②,根据一组对边平行且相等的四边形是平行四边形,可判断四边形ABCD成为平行四边形
B、①③,根据两组对边平行的四边形是平行四边形,可判断四边形ABCD成为平行四边形
C、①④,不能判断四边形ABCD成为平行四边形
D、②④,根据两组对边相等的四边形是平行四边形,可判断四边形ABCD成为平行四边形
故选C.
8.D
【解析】试题解析:如图,则可得对角线EF⊥AD,且EF与平行四边形的高相等.
∵平行四边形纸片ABCD的面积为60,
∴S△AOD+S△BOC=SABCD=30,
∴EF×BC=S△AOD+S△BOC=30,
∴对角线之积为60.
故选D.
9.C
【解析】根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和三角形内角和定理即可求出∠PMN的度数.
解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN,∴△PMN是等腰三角形.
∵∠MPN=130°,∴∠PMN==25°.
故选C.
10.D
【解析】(1)∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠ADF=∠ABE=60°,
∴DF=BC,CD=BE,
∠CDF=360°-∠ADC-60°=300°-∠ADC,∠EBC=360°-∠ABC-60°=300°-∠ABC,
∴∠CDF=∠EBC,
∴△CDF≌△EBC(SAS),故A中结论正确;
(2)∵在平行四边形ABCD中,∠DAB=180°-∠ADC,
∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,
又∵∠CDF=300°-∠ADC,
∴∠CDF=∠EAF,故B中结论正确;
(3)∵在△CDF和△EAF中,DF=AF,∠CDF=∠EAF,DC=AB=AE,
∴△CDF≌△EAF,
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EF=CE=CF,
∴△ECF是等边三角形,故C正确;
(4)∵△ABE是等边三角形,
∴∠ABE=60°,
∴当CG⊥AE时,∠ABG=30°,
则此时∠ABC=180°-∠ABG=150°,
∵由题中条件无法确定∠ABC的度数,
∴D中结论不一定成立.
故选D.
11.(1,﹣1)
【解析】直接利用x轴上点的坐标特点得出n的值,进而利用关于原点对称点的性质得出答案.
解:∵点A(﹣2,n)在x轴上,
∴n=0,
∴B(﹣1,1)
则点B(n﹣1,n+1)关于原点对称的点的坐标为:(1,﹣1).
故答案为:(1,﹣1).
12.360°
【解析】根据三角形外角的性质可知:∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,利用多边形外角和为360°即可求出结果.
解:如图:
根据三角形外角的性质可知:∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,
∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故答案为:360°.
13.假设三角形三个内角都小于60度
【解析】
反证法的第一步是假设命题的结论不成立,据此可以得到答案.
解:
用反证法证明“三角形中必有一个内角不小于60°”时,应先假设三角形中每一个内角都小于60°.
故答案为:三角形中每一个内角都小于60°
14.或4
【解析】根据三角函数可以计算出,,再根据中位线的性质可得,,,然后拼图,出现两种情况,一种是拼成一个矩形,另一种拼成一个平行四边形,进而算出周长即可.
解:由题意可得:,
,
,,
图中所示的中位线剪开,
,,,
如图1所示:
拼成一个矩形,矩形周长为:;
如图2所示,
可以拼成一个平行四边形,周长为:,
故答案为4或.
15.三、四、五
【解析】如图可知,一个四边形截去一个三角形后变成三角形或四边形或五边形,
故答案为:三、四、五.
16.2或
【解析】由已知以点P,Q,E,D为顶点的四边形是平行四边形有两种情况,(1)当Q运动到E和B之间,(2)当Q运动到E和C之间,根据平行四边形的判定,由AD∥BC,所以当PD=QE时为平行四边形.据此设运动时间为t,列出关于t的方程求解.
解:由已知梯形,
当Q运动到E和B之间,设运动时间为t,则得:=6-t,
解得:t=,
当Q运动到E和C之间,设运动时间为t,则得:-2t=6-t,
解得:t=2,
故当运动时间t为2或秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
故答案为2或
17.见解析
【解析】首先根据平行四边形ABCD的性质得到AB和CD平行且相等,结合已知条件发现DF和BE平行且相等.证明四边形DEBF为平行四边形.得到DE和BF平行且相等,再结合中点的概念,所以四边形MENF为平行四边形.
证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD,
∴BE∥DF,
∵
AE=CF,
∴
BE=DF,
∴四边形BEDF是平行四边形
∴DE∥BF
,DE=BF,
∵点M,N分别是DE,BF中点,
∴EM=DE,
FN=BF,
∴EM=FN,
∵EM∥FN,
∴四边形EMFN是平行四边形.
18.(1)画图见解析;(2)(2,-1).
【解析】(1)、根据网格结构找出点A、B关于点C成中心对称的点A1、B1的位置,再与点A顺次连接即可;根据网格结构找出点A、B、C平移后的对应点A2、B2、C2的位置,然后顺次连接即可;(2)、根据中心对称的性质,连接两组对应点的交点即为对称中心.
解:(1)、△A1B1C如图所示,
△A2B2C2如图所示;
(2)、如图,对称中心为(2,﹣1).
19.(1)∠DAF=30°;(2)见解析.
【解析】(1)根据平行四边形的性质与三角形的内角和即可求解;
(2)根据AAS即可证明三角形全等.
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC=40°.
∵∠AFD+∠AFE=180°,
∴∠AFD=180°﹣∠AFE=110°,
∴∠DAF=180°﹣∠ADF﹣∠AFD=30°;
(2)证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC,
∵∠AFD+∠AFE=180°,∠AFE=∠ADC,
∴∠AFD=∠C,
在△AFD和△DEC中,,
∴△AFD≌△DCE(AAS).
20.(1)∠D'EF=76°;(2).
【解析】(1)根据折叠的性质可得:∠D=∠ED'G=60°,∠DEF=∠D'EF,根据平行线的性质有∠DEF=∠EFB.等量代换得到∠D'EF=∠EFB,在四边形中,根据四边形的内角和即可求解.
(2)过点E作EH⊥AB于点H,设AE=x,根据平行线的性质有∠HAD=∠B=60°,且EH⊥AB,求出
根据中点的性质有根据勾股定理即可求解.
解:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AD∥BC,
∴∠DEF=∠EFB.
∵将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,
∴∠D=∠ED'G=60°,∠DEF=∠D'EF,
∴∠D'EF=∠EFB,
∵∠BGD′=32°
∴∠D'GF=148°
∵∠D'GF+∠EFB+∠D'EF+∠ED'G=360°,
,
∴∠D'EF=76°;
(2)过点E作EH⊥AB于点H,
设AE=x,
∵AD∥BC,
∴∠HAD=∠B=60°,且EH⊥AB,
∴
∵点D'是AB中点,
∴
∵HE2+D'H2=D'E2,
∴
∴x=,
∴.
21.(1)因为2014°不是180°的整数倍,所以小明说不可能;(2)13;(3)34°.
【解析】解决本题的关键是正确记忆运用多边形的内角和公式,是需要熟记的内容.n边形的内角和是(n-2)?180°,因而内角和一定是180度的倍数.而多边形的内角一定大于0,并且小于180度,因而内角和再加上一个内角的值,这个值除以180度,所得数值比边数n-2要大,大的值小于1.则用内角和于内角的和除以180所得值,加上2,比这个数小的最大的整数就是多边形的边数.
解:(1)∵n边形的内角和是(n﹣2)?180°,∴内角和一定是180度的倍数,
∵2014÷180=11…34,∴内角和为2014°不可能;
(2)依题意有(x﹣2)?180°<2014°,解得x<13.
因而多边形的边数是13,
故小华求的是十三边形的内角和;
(2)13边形的内角和是(13﹣2)×180°=1980°,2014°﹣1980°=34°,因此这个外角的度数为34°.[
22.(1)26;(2)见解析
【解析】(1)由平行四边形的性质得出AD=BC=8,AB=CD,AD∥BC,由平行线的性质得出∠AEB=∠CBE,由BE平分∠ABC,得出∠ABE=∠CBE,推出∠ABE=∠AEB,则AB=AE,AE=AD﹣ED=BC﹣ED=5,得出AB=5,即可得出结果;
(2)连接CE,过点C作CK∥BF交BE于K,则∠FBG=∠CKG,由点G是CF的中点,得出FG=CG,由AAS证得△FBG≌△CKG,得出BG=KG,CK=BF=CD,由平行四边形的性质得出∠ABC=∠D,∠BAE+∠D=180°,AB=CD=CK,AD∥BC,由平行线的性质得出∠DEC=∠BCE,∠AEB=∠KBC,易证∠EKC=∠D,∠CKB=∠BAE,由AAS证得△AEB≌△KBC,得出BC=BE,则∠KEC=∠BCE,推出∠KEC=∠DEC,由AAS证得△KEC≌△DEC,得出KE=ED,即可得出结论.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC=8,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵AE=AD﹣ED=BC﹣ED=8﹣3=5,
∴AB=5,
∴平行四边形ABCD的周长=2AB+2BC=2×5+2×8=26;
(2)连接CE,过点C作CK∥BF交BE于K,如图2所示:
则∠FBG=∠CKG,
∵点G是CF的中点,
∴FG=CG,
在△FBG和△CKG中,
∵
,
∴△FBG≌△CKG(AAS),
∴BG=KG,CK=BF=CD,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D,∠BAE+∠D=180°,AB=CD=CK,AD∥BC,
∴∠DEC=∠BCE,∠AEB=∠KBC,
∵∠FBE+∠ABC=180°,
∴∠FBE+∠D=180°,
∴∠CKB+∠D=180°,
∴∠EKC=∠D,
∵∠BAE+∠D=180°,
∴∠CKB=∠BAE,
在△AEB和△KBC中,
∵,
∴△AEB≌△KBC(AAS),
∴BC=EB,
∴∠KEC=∠BCE,
∴∠KEC=∠DEC,
在△KEC和△DEC中,
∵,
∴△KEC≌△DEC(AAS),
∴KE=ED,
∵BE=BG+KG+KE=2BG+ED,
∴2BG+ED=BC.
23.(1)120,135,;(2)∠P=;(3);(4);(5)
【解析】(1)根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;(2)根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理(1)解答即可;(3)根据五边形的内角和公式表示出∠ADC+∠BCD,然后同理(1)解答即可;(4)根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理(1)解答即可;(5)根据n边形的内角和公式表示出∠ADC+∠BCD,然后同理(1)解答即可.
解:(1)∵DP、CP分别平分∠ADC和∠ACD,
∴,,
∴∠P=180°-∠PDC-∠PCD
∴如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则;
故答案为120,135,;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴,,
∴∠P=180°-∠PDC-∠PCD
;
即∠P=;
(3)五边形ABCDEF的内角和为:(5-2)×180°=540°,
∵DP、CP分别平分∠ADC和∠ACD,
∴,,
∴∠P=180°-∠PDC-∠PCD
故答案为即.
(4)六边形ABCDEF的内角和为:(6-2)×180°=720°,
∵DP、CP分别平分∠ADC和∠ACD,
∴,,
∴∠P=180°-∠PDC-∠PCD,
故答案为
(5)同(1)可得,;
故答案为
24.(1)60°;(2);(3)当运动时间为4.8秒或8秒或9.6秒时,以四点组成的四边形是平行四边形.
【解析】(1)只要证明△PCD是等边三角形即可;
(2)由四边形ABCD是平行四边形,推出,,推出S△PBC=S△FAB=S平行四边形ABCD,推出S△ABP+S△PCD=S平行四边形ABCD,推出S△APF+S△ABP=S△ABP+S△PCD,可得S△APF=S△PCD由此即可解决问题;
(3分四种情形列出方程解方程即可.
解:(1)四边形是平行四边形,
,
,
平分,
,
,
.
,
,
是等边三角形,
.
(2)四边形是平行四边形,
,,,
,
,
,
.
(3)四边形是平行四边形,
,
.
若要使四边形是平行四边形,则,
设运动时间为秒,
①当时,,,
,解得,不合题意,舍去;
②当时,,,
,解得;
③当时,,,
,解得;
④当时,,,
,解得;
综上所述:当运动时间为4.8秒或8秒或9.6秒时,以四点组成的四边形是平行四边形.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第14页
【单元双测卷——能力测】
第四章
平行四边形
说明:全卷满分120分,有三大题,共24小题.
班级:__________
姓名:__________
得分:__________
一、选择题(本题有10小题,每题3分,共30分.
请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下列图形均是一些科技创新公司标志图,其中既是中心对称图形又是轴对称图形的是(
)
A.
B.??
C.?????
D.
2.在下列性质中,平行四边形不一定具有的是(
)
A.对边相等
B.对角互补
C.对边平行
D.对角相等
3.如图,
中,,平分交
边于点,且
,则
的长为(
)
A.3
B.4
C.2
D.5
第3题图
第4题图
第6题图
4.如图,ABCD中,E,F分别是AB,CD的中点,则图中有________个平行四边形.(
)
A.7个
B.8个
C.9个
D.10个
5.把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为(
)
A.9
B.10
C.11
D.以上都有可能
6.如图,平面直角坐标系中,平行四边形ABCD的中心E的坐标为(2,0),若点A的坐标为(-2,1),则点C的坐标为(
)
A.(4,-1)
B.(6,-1)
C.(8,-1)
D.(6,-2)
7.已知四边形ABCD中有四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从中任选两个,不能使四边形ABCD成为平行四边形的是(
)
A.①②
B.①③
C.①④
D.②④
8.如图①,平行四边形纸片ABCD的面积为60,沿对角线AC,BD将其裁剪成四个三角形纸片,将纸片△AOD翻转后,与纸片△COB拼接成如图②所示的四边形(点A与点C,点D与点B重合),则拼接后的四边形的两条对角线之积为(
)
A.30
B.40
C.50
D.60
第8题图
第9题图
第10题图
9.如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为(
)
A.10°
B.15°
C.25°
D.40°
10.如图,已知在?ABCD中,分别以AB,AD为边分别向外作等边三角形ABE和等边三角形ADF,延长CB交AE于点G,点G在点A,E之间,连接CE,CF,EF,则下列结论不一定正确的是(
)
A.△CDF≌△EBC
B.∠CDF=∠EAF
C.△ECF是等边三角形
D.CG⊥AE
二、填空题(本题有6小题,每题4分,共24分)
11.若点A(﹣2,n)在x轴上,则点B(n﹣1,n+1)关于原点对称的点的坐标为_____.
12.如图,∠A+∠B+∠C+∠D+∠E+∠F=__________.
第12题图
第14题图
第16题图
13.用反证法证明“三角形中必有一个内角不小于60°”,应当先假设这个三角形中_________.
14.如图,有一张直角三角形纸片,,,,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是______.
15.一个四边形剪去一三角形后余下的多边形为
___________
边形
16.如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
三、解答题(本题有8小题,共66分.解答应写出文字说明、证明过程或演算步骤)
17.(本题6分)如图,在
□ABCD中,E,F分别是边AB,CD上的点.已知AE=CF,M,N分别是DE和FB的中点.求证:四边形ENFM是平行四边形.
18.(本题6分)如图,在平面直角坐标系中,的三个顶点分别是、、.
(1)画出关于点成中心对称的△;平移,若点的对应点的坐标为,画出平移后对应的△;
(2)△和△关于某一点成中心对称,则对称中心的坐标为
.
19.(本题8分)如图,在平行四边形ABCD中,点E是BC上的一点,F在线段DE上,且∠AFE=∠ADC.
(1)若∠AFE=70°,∠DEC=40°,求∠DAF的大小;
(2)若DE=AD,求证:△AFD≌△DCE
20.(本题8分)如图,在平行四边形ABCD中,AB=,BC=8,∠B=60°,将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,折叠后点C的对应点为C′,D′C′交BC于点G,∠BGD′=32°.
(1)求∠D′EF的度数;
(2)求线段AE的长.
21.(本题8分)看图回答问题:
(1)内角和为2014°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?它是多少度?
22.(本题10分)在平行四边形ABCD中,点E是AD边上的点,连接BE.
(1)如图1,若BE平分∠ABC,BC=8,ED=3,求平行四边形ABCD的周长;
(2)如图2,点F是平行四边形外一点,FB=CD.连接BF、CF,CF与BE相交于点G,若∠FBE+∠ABC=180°,点G是CF的中点,求证:2BG+ED=BC.
23.(本题10分)(1)已知:如图1,P为内一点,DP、CP分别平分和,如果,那么________;如果,那么________;如果,则________;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分和,试探究与的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平分和,请直接写出与的数量关系:________________;
(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平分和,请直接写出与的数量关系:________________;
(5)若P为n边形内一点,平分,平分,请直接写出与的数量关系:________________.(用含n的代数式表示)
24.(本题10分)已知在中,动点在边上,以每秒的速度从点向点运动.
(1)如图1,在运动过程中,若平分,且满足,求的度数.
(2)如图2,在(1)的条件下,连结并延长与的延长线交于点,连结,若,求的面积.
(3)如图3,另一动点在边上,以每秒的速度从点出发,在间往返运动,两点同时出发,当点到达点时停止运动(同时点也停止),若,求当运动时间为多少秒时,以D,四点组成的四边形是平行四边形.
答案及解析
1.D
【解析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.
解:A、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误;
B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
C、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.
故选D.
2.B
【解析】根据平行四边形的性质逐项排除即可.
解:∵平行四边形的对边平行、对角相等、对边相等,
∴选项B不正确;
故答案为B.
3.B
【解析】求证DC=DE,再由平行四边形得AD=BC,即可求出AB长.
解:∵四边形ABCD为平行四边形,
∴AD=BC=7,AD∥BC,DC=AB,
∴∠DEC=∠ECB,
∵平分,
∴∠ECB=∠ECD,
∴∠DEC=∠DCE,
∴DE=DC,
∵AE=3,
∴DE=7-3=4,
∴AB=CD=DE=4,
故选B.
4.B
【解析】根据平行四边的判定及中位线定理,利用三角形全等,可推出8个平行四边形.
解:E,F分别是AD,BC的中点,则有,
∴四边形AECF,EDFB,是平行四边形,有∠FBE=∠EDF=∠AEB,
∵AE∥BF
∴EAF=∠AFB
∴根据ASA得出△MAE≌△MFB,∴AM=MF,即点M是AF的中点,
同理,点N是FD的中点,∴MN是△EBC和△AFD的中位线,∴,
∴四边形AENM,DEMN,BMNF,FCNM是平行四边形
∵EN∥MF,ME∥FN
∴四边形ENFM是平行四边形,而四边形ABCD也是平行四边形,共8个平行四边形.
故选B.
5.D
【解析】设新多边形的边数为n,则由题意可得:180(n-2)=1440,解得:n=10,
∵多边形截去一个角之后,新多边形的边数可能和原多边形相同,可能比原多边形多一边,也可能比原多边形少一边,
∴原多边形的边数可能是9或10或11.
故选D.
6.B
【解析】首先连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,E是平行四边形ABCD的中心,即可得AC过点E,易证得△AEG≌△CEH,继而求得答案.
解:连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,
∵E是平行四边形ABCD的中心,
∴AC过点E,
∴AE=CE,
在△AEG和△CEH中,
,
∴△AEG≌△CEH(AAS),
∴EG=EH,CH=AG,
∵E的坐标为(2,0),点A的坐标为(-2,1),
∴EH=EG=4,CH=AG=1,
∴OH=OE+EH=6,
∴点C的坐标为:(6,-1).
故选B.
7.C
【解析】根据平行四边形的判定可直接判断.
解:A、①②,根据一组对边平行且相等的四边形是平行四边形,可判断四边形ABCD成为平行四边形
B、①③,根据两组对边平行的四边形是平行四边形,可判断四边形ABCD成为平行四边形
C、①④,不能判断四边形ABCD成为平行四边形
D、②④,根据两组对边相等的四边形是平行四边形,可判断四边形ABCD成为平行四边形
故选C.
8.D
【解析】试题解析:如图,则可得对角线EF⊥AD,且EF与平行四边形的高相等.
∵平行四边形纸片ABCD的面积为60,
∴S△AOD+S△BOC=SABCD=30,
∴EF×BC=S△AOD+S△BOC=30,
∴对角线之积为60.
故选D.
9.C
【解析】根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和三角形内角和定理即可求出∠PMN的度数.
解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN,∴△PMN是等腰三角形.
∵∠MPN=130°,∴∠PMN==25°.
故选C.
10.D
【解析】(1)∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠ADF=∠ABE=60°,
∴DF=BC,CD=BE,
∠CDF=360°-∠ADC-60°=300°-∠ADC,∠EBC=360°-∠ABC-60°=300°-∠ABC,
∴∠CDF=∠EBC,
∴△CDF≌△EBC(SAS),故A中结论正确;
(2)∵在平行四边形ABCD中,∠DAB=180°-∠ADC,
∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,
又∵∠CDF=300°-∠ADC,
∴∠CDF=∠EAF,故B中结论正确;
(3)∵在△CDF和△EAF中,DF=AF,∠CDF=∠EAF,DC=AB=AE,
∴△CDF≌△EAF,
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EF=CE=CF,
∴△ECF是等边三角形,故C正确;
(4)∵△ABE是等边三角形,
∴∠ABE=60°,
∴当CG⊥AE时,∠ABG=30°,
则此时∠ABC=180°-∠ABG=150°,
∵由题中条件无法确定∠ABC的度数,
∴D中结论不一定成立.
故选D.
11.(1,﹣1)
【解析】直接利用x轴上点的坐标特点得出n的值,进而利用关于原点对称点的性质得出答案.
解:∵点A(﹣2,n)在x轴上,
∴n=0,
∴B(﹣1,1)
则点B(n﹣1,n+1)关于原点对称的点的坐标为:(1,﹣1).
故答案为:(1,﹣1).
12.360°
【解析】根据三角形外角的性质可知:∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,利用多边形外角和为360°即可求出结果.
解:如图:
根据三角形外角的性质可知:∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,
∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故答案为:360°.
13.假设三角形三个内角都小于60度
【解析】
反证法的第一步是假设命题的结论不成立,据此可以得到答案.
解:
用反证法证明“三角形中必有一个内角不小于60°”时,应先假设三角形中每一个内角都小于60°.
故答案为:三角形中每一个内角都小于60°
14.或4
【解析】根据三角函数可以计算出,,再根据中位线的性质可得,,,然后拼图,出现两种情况,一种是拼成一个矩形,另一种拼成一个平行四边形,进而算出周长即可.
解:由题意可得:,
,
,,
图中所示的中位线剪开,
,,,
如图1所示:
拼成一个矩形,矩形周长为:;
如图2所示,
可以拼成一个平行四边形,周长为:,
故答案为4或.
15.三、四、五
【解析】如图可知,一个四边形截去一个三角形后变成三角形或四边形或五边形,
故答案为:三、四、五.
16.2或
【解析】由已知以点P,Q,E,D为顶点的四边形是平行四边形有两种情况,(1)当Q运动到E和B之间,(2)当Q运动到E和C之间,根据平行四边形的判定,由AD∥BC,所以当PD=QE时为平行四边形.据此设运动时间为t,列出关于t的方程求解.
解:由已知梯形,
当Q运动到E和B之间,设运动时间为t,则得:=6-t,
解得:t=,
当Q运动到E和C之间,设运动时间为t,则得:-2t=6-t,
解得:t=2,
故当运动时间t为2或秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
故答案为2或
17.见解析
【解析】首先根据平行四边形ABCD的性质得到AB和CD平行且相等,结合已知条件发现DF和BE平行且相等.证明四边形DEBF为平行四边形.得到DE和BF平行且相等,再结合中点的概念,所以四边形MENF为平行四边形.
证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD,
∴BE∥DF,
∵
AE=CF,
∴
BE=DF,
∴四边形BEDF是平行四边形
∴DE∥BF
,DE=BF,
∵点M,N分别是DE,BF中点,
∴EM=DE,
FN=BF,
∴EM=FN,
∵EM∥FN,
∴四边形EMFN是平行四边形.
18.(1)画图见解析;(2)(2,-1).
【解析】(1)、根据网格结构找出点A、B关于点C成中心对称的点A1、B1的位置,再与点A顺次连接即可;根据网格结构找出点A、B、C平移后的对应点A2、B2、C2的位置,然后顺次连接即可;(2)、根据中心对称的性质,连接两组对应点的交点即为对称中心.
解:(1)、△A1B1C如图所示,
△A2B2C2如图所示;
(2)、如图,对称中心为(2,﹣1).
19.(1)∠DAF=30°;(2)见解析.
【解析】(1)根据平行四边形的性质与三角形的内角和即可求解;
(2)根据AAS即可证明三角形全等.
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC=40°.
∵∠AFD+∠AFE=180°,
∴∠AFD=180°﹣∠AFE=110°,
∴∠DAF=180°﹣∠ADF﹣∠AFD=30°;
(2)证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC,
∵∠AFD+∠AFE=180°,∠AFE=∠ADC,
∴∠AFD=∠C,
在△AFD和△DEC中,,
∴△AFD≌△DCE(AAS).
20.(1)∠D'EF=76°;(2).
【解析】(1)根据折叠的性质可得:∠D=∠ED'G=60°,∠DEF=∠D'EF,根据平行线的性质有∠DEF=∠EFB.等量代换得到∠D'EF=∠EFB,在四边形中,根据四边形的内角和即可求解.
(2)过点E作EH⊥AB于点H,设AE=x,根据平行线的性质有∠HAD=∠B=60°,且EH⊥AB,求出
根据中点的性质有根据勾股定理即可求解.
解:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AD∥BC,
∴∠DEF=∠EFB.
∵将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,
∴∠D=∠ED'G=60°,∠DEF=∠D'EF,
∴∠D'EF=∠EFB,
∵∠BGD′=32°
∴∠D'GF=148°
∵∠D'GF+∠EFB+∠D'EF+∠ED'G=360°,
,
∴∠D'EF=76°;
(2)过点E作EH⊥AB于点H,
设AE=x,
∵AD∥BC,
∴∠HAD=∠B=60°,且EH⊥AB,
∴
∵点D'是AB中点,
∴
∵HE2+D'H2=D'E2,
∴
∴x=,
∴.
21.(1)因为2014°不是180°的整数倍,所以小明说不可能;(2)13;(3)34°.
【解析】解决本题的关键是正确记忆运用多边形的内角和公式,是需要熟记的内容.n边形的内角和是(n-2)?180°,因而内角和一定是180度的倍数.而多边形的内角一定大于0,并且小于180度,因而内角和再加上一个内角的值,这个值除以180度,所得数值比边数n-2要大,大的值小于1.则用内角和于内角的和除以180所得值,加上2,比这个数小的最大的整数就是多边形的边数.
解:(1)∵n边形的内角和是(n﹣2)?180°,∴内角和一定是180度的倍数,
∵2014÷180=11…34,∴内角和为2014°不可能;
(2)依题意有(x﹣2)?180°<2014°,解得x<13.
因而多边形的边数是13,
故小华求的是十三边形的内角和;
(2)13边形的内角和是(13﹣2)×180°=1980°,2014°﹣1980°=34°,因此这个外角的度数为34°.[
22.(1)26;(2)见解析
【解析】(1)由平行四边形的性质得出AD=BC=8,AB=CD,AD∥BC,由平行线的性质得出∠AEB=∠CBE,由BE平分∠ABC,得出∠ABE=∠CBE,推出∠ABE=∠AEB,则AB=AE,AE=AD﹣ED=BC﹣ED=5,得出AB=5,即可得出结果;
(2)连接CE,过点C作CK∥BF交BE于K,则∠FBG=∠CKG,由点G是CF的中点,得出FG=CG,由AAS证得△FBG≌△CKG,得出BG=KG,CK=BF=CD,由平行四边形的性质得出∠ABC=∠D,∠BAE+∠D=180°,AB=CD=CK,AD∥BC,由平行线的性质得出∠DEC=∠BCE,∠AEB=∠KBC,易证∠EKC=∠D,∠CKB=∠BAE,由AAS证得△AEB≌△KBC,得出BC=BE,则∠KEC=∠BCE,推出∠KEC=∠DEC,由AAS证得△KEC≌△DEC,得出KE=ED,即可得出结论.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC=8,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵AE=AD﹣ED=BC﹣ED=8﹣3=5,
∴AB=5,
∴平行四边形ABCD的周长=2AB+2BC=2×5+2×8=26;
(2)连接CE,过点C作CK∥BF交BE于K,如图2所示:
则∠FBG=∠CKG,
∵点G是CF的中点,
∴FG=CG,
在△FBG和△CKG中,
∵
,
∴△FBG≌△CKG(AAS),
∴BG=KG,CK=BF=CD,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D,∠BAE+∠D=180°,AB=CD=CK,AD∥BC,
∴∠DEC=∠BCE,∠AEB=∠KBC,
∵∠FBE+∠ABC=180°,
∴∠FBE+∠D=180°,
∴∠CKB+∠D=180°,
∴∠EKC=∠D,
∵∠BAE+∠D=180°,
∴∠CKB=∠BAE,
在△AEB和△KBC中,
∵,
∴△AEB≌△KBC(AAS),
∴BC=EB,
∴∠KEC=∠BCE,
∴∠KEC=∠DEC,
在△KEC和△DEC中,
∵,
∴△KEC≌△DEC(AAS),
∴KE=ED,
∵BE=BG+KG+KE=2BG+ED,
∴2BG+ED=BC.
23.(1)120,135,;(2)∠P=;(3);(4);(5)
【解析】(1)根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;(2)根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理(1)解答即可;(3)根据五边形的内角和公式表示出∠ADC+∠BCD,然后同理(1)解答即可;(4)根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理(1)解答即可;(5)根据n边形的内角和公式表示出∠ADC+∠BCD,然后同理(1)解答即可.
解:(1)∵DP、CP分别平分∠ADC和∠ACD,
∴,,
∴∠P=180°-∠PDC-∠PCD
∴如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则;
故答案为120,135,;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴,,
∴∠P=180°-∠PDC-∠PCD
;
即∠P=;
(3)五边形ABCDEF的内角和为:(5-2)×180°=540°,
∵DP、CP分别平分∠ADC和∠ACD,
∴,,
∴∠P=180°-∠PDC-∠PCD
故答案为即.
(4)六边形ABCDEF的内角和为:(6-2)×180°=720°,
∵DP、CP分别平分∠ADC和∠ACD,
∴,,
∴∠P=180°-∠PDC-∠PCD,
故答案为
(5)同(1)可得,;
故答案为
24.(1)60°;(2);(3)当运动时间为4.8秒或8秒或9.6秒时,以四点组成的四边形是平行四边形.
【解析】(1)只要证明△PCD是等边三角形即可;
(2)由四边形ABCD是平行四边形,推出,,推出S△PBC=S△FAB=S平行四边形ABCD,推出S△ABP+S△PCD=S平行四边形ABCD,推出S△APF+S△ABP=S△ABP+S△PCD,可得S△APF=S△PCD由此即可解决问题;
(3分四种情形列出方程解方程即可.
解:(1)四边形是平行四边形,
,
,
平分,
,
,
.
,
,
是等边三角形,
.
(2)四边形是平行四边形,
,,,
,
,
,
.
(3)四边形是平行四边形,
,
.
若要使四边形是平行四边形,则,
设运动时间为秒,
①当时,,,
,解得,不合题意,舍去;
②当时,,,
,解得;
③当时,,,
,解得;
④当时,,,
,解得;
综上所述:当运动时间为4.8秒或8秒或9.6秒时,以四点组成的四边形是平行四边形.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第14页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
