5.4中心对称

(共37张PPT)
我们已学过哪些图形变换？
轴对称变换、平移变换、旋转变换、相似变换。
这幅图案有哪些变换？
90°、180°、270°。
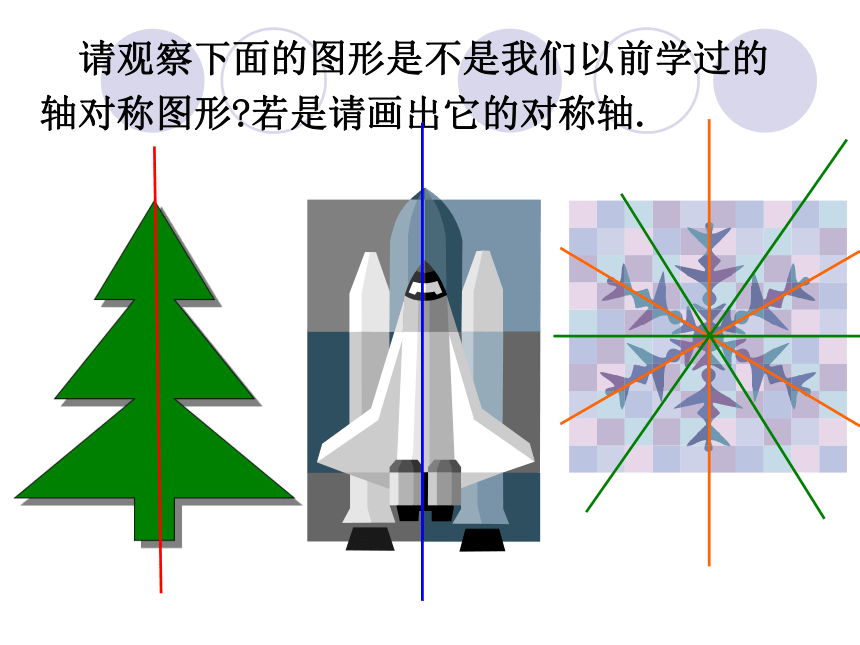
请观察下面的图形是不是我们以前学过的轴对称图形 若是请画出它的对称轴.
你能从下面车标中看到它们运用了哪些图形变换？
你认识这些车标吗？
这些图标旋转几度可以与自身重合？
如果一个图形绕着一个点旋转1800后,所得到的图形能够和原图形互相重合,那么这个图形叫做中心对称图形。
C
O/
D
A
B
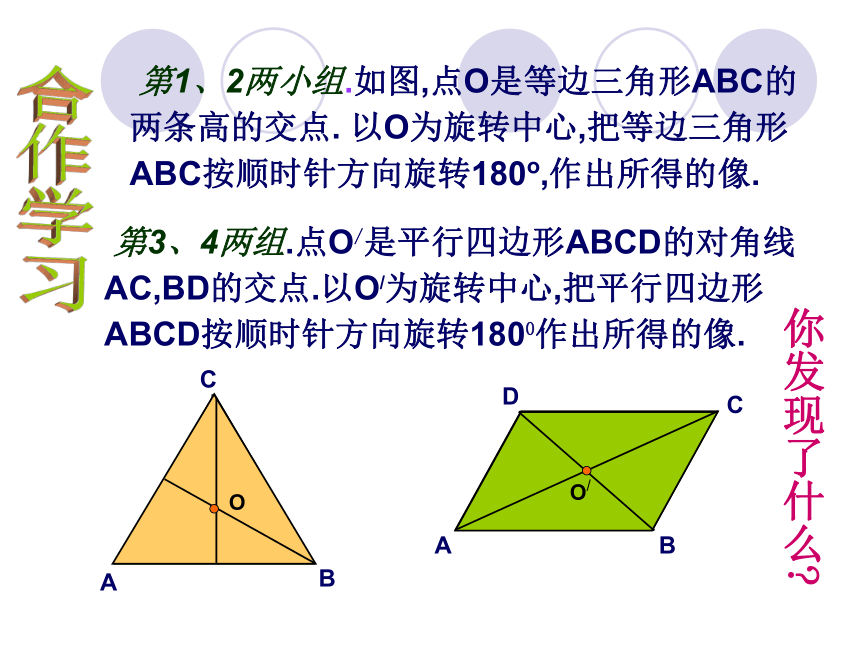
第1、2两小组.如图,点O是等边三角形ABC的两条高的交点. 以O为旋转中心,把等边三角形ABC按顺时针方向旋转180o,作出所得的像.
第3、4两组.点O/是平行四边形ABCD的对角线AC,BD的交点.以O/为旋转中心,把平行四边形ABCD按顺时针方向旋转1800作出所得的像.
C
A
B
你发现了什么
O/
O
C
O/
D
A
B
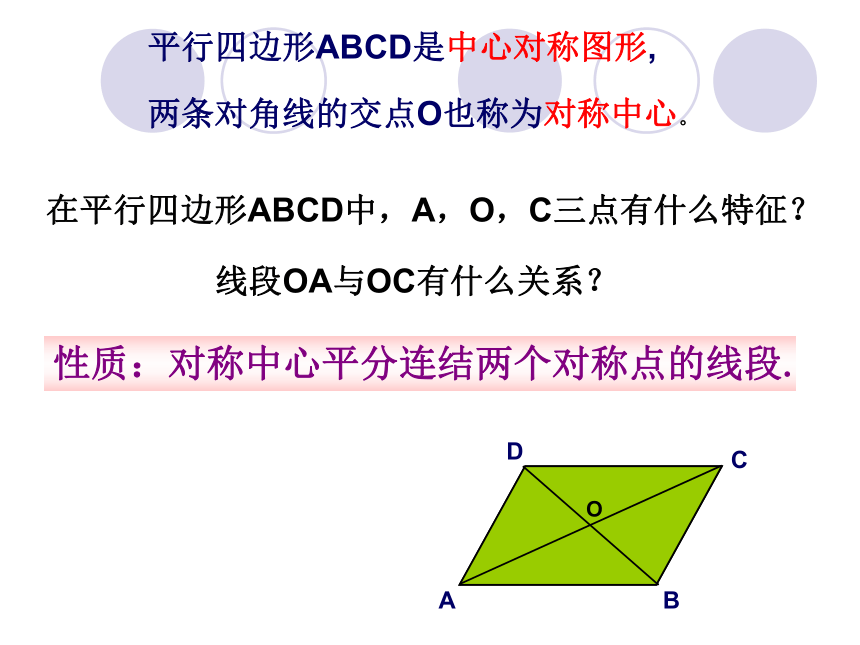
平行四边形ABCD是中心对称图形,
两条对角线的交点O也称为对称中心。
O
性质：对称中心平分连结两个对称点的线段.
线段OA与OC有什么关系？
在平行四边形ABCD中，A，O，C三点有什么特征？
下列哪些图形是轴对称图形
(1)
(8)
(7)
(6)
(5)
(4)
(3)
(2)
哪些图形是中心对称图形
哪些图形既是中心对称图形 又是轴对称图形？
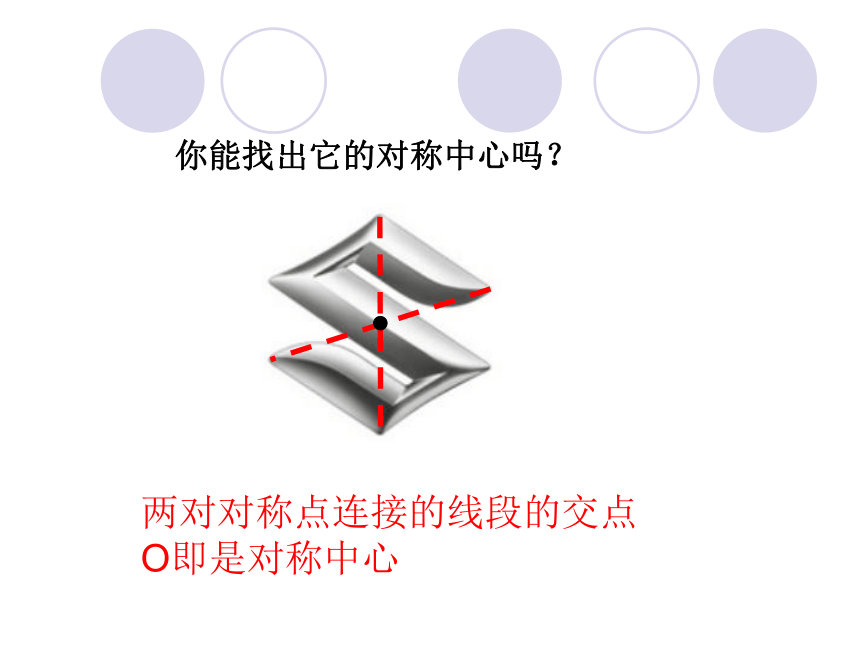
你能找出它的对称中心吗？
两对对称点连接的线段的交点O即是对称中心
A
O
A'
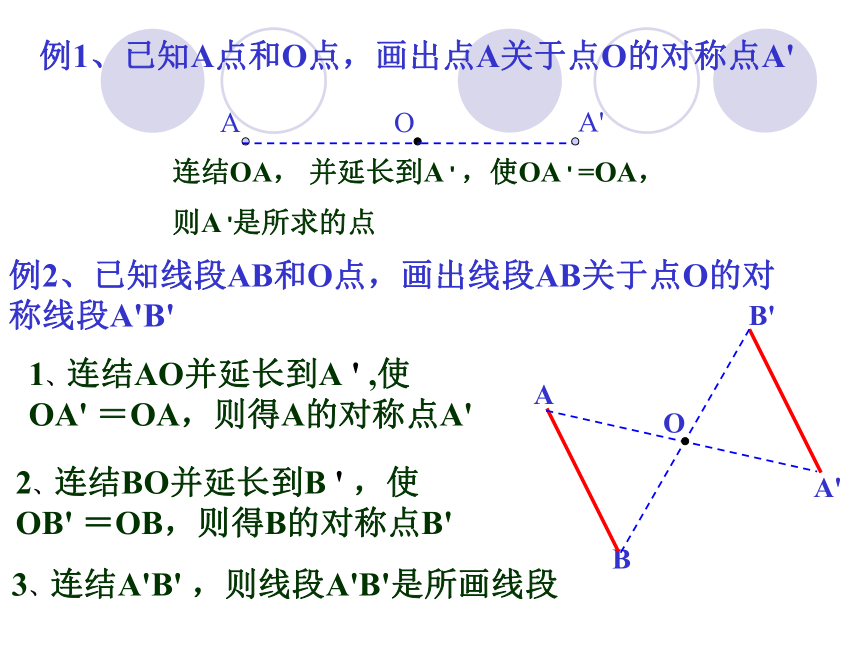
连结OA，
并延长到A ' ，使OA ' =OA，
例1、已知A点和O点，画出点A关于点O的对称点A'
则A '是所求的点
例2、已知线段AB和O点，画出线段AB关于点O的对称线段A'B'
O
A'
B'
A
B
1、连结AO并延长到A ' ,使 OA' ＝OA，则得A的对称点A'
2、连结BO并延长到B ' ，使OB' ＝OB，则得B的对称点B'
3、连结A'B' ，则线段A'B'是所画线段
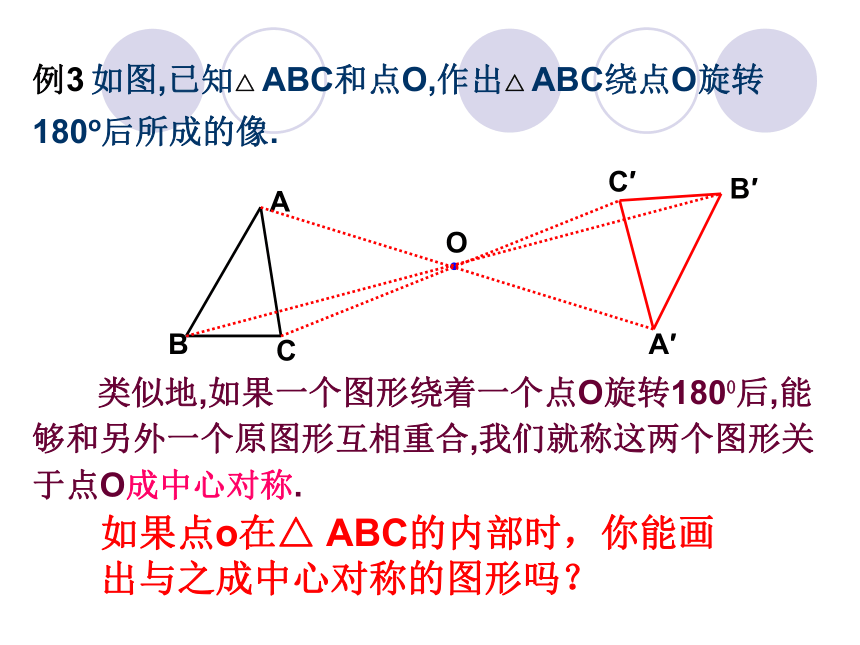
例3 如图,已知△ ABC和点O,作出△ ABC绕点O旋转180o后所成的像.
(2)同理,作出点B,C的对称点B/,C/;
解:(1)连结AO关延长到A/,使AO=A/O;
(3)连结A/B/.B/C/,C/A/,则⊿A/B/C/即为所求的三角形.
A
B
C
O
A′
C′
B′
类似地,如果一个图形绕着一个点O旋转1800后,能够和另外一个原图形互相重合,我们就称这两个图形关于点O成中心对称.
如果点o在△ ABC的内部时，你能画出与之成中心对称的图形吗？
例4、已知四边形ABCD和点O，画四边形A′B′C′D′，使它与已知四边形关于这一点对称。
A
B
A’
C’
B’
D’
D
O
C
四边形A/B/C/D/即为所求的图形。
A
B
C
A’
B’
C’
做一做
1、如图，已知△ABC与△A’B’C’中心对称，求出它们的对称中心O。
2、你能很快地找到点E的对应点F吗？
Ａ
Ｂ
Ｃ
Ｄ
Ｏ
Ｅ
·
Ｆ
OE=OF成立吗？
EF经过点O，分别交AB、CD于E、F。
解：∵平行四边形是中心对称图形，O是对称中心
∴点E、F是关于点O的对称点 ∴OE=OF
3、画一个与已知四边形ABCD中心对称图形。
（1）以顶点A为对称中心；
（2）以BC边的中点为对称中心。
D
A
B
C
E
F
G
M
D
A
B
C
O
．
N
做一做
A’
B’
C’
O
A
B
C
4、如图，已知等边三角形ABC和点O，画△A’B’C’,使△A’B’C’和△ABC关于点O成中心对称。
做一做
下面的扑克牌中，哪些牌面是中心对称图形？
在下列英文大写正体字母中，哪些字母是中心对称图形？
A B E F I J
N R S T X Z
如图是五个小正方形拼成的图形.请你移动其中一个小正方形,重新拼成一个图形,使得所拼成的新图形:
(1)是轴对称图形,但不是中心对称图形。
(2)是中心对称图形,但不是轴对称图形
(3)既是轴对称图形,又是中心对称图形
(1)
(2)
(3)
1
2
3
4
游戏：把其中的一张纸牌旋转 后
仍和原来一样，请你猜猜旋转了哪一张？
练习
如图，在平行四边形ABCD中，AC与BD交于点O，过点O的两条直线，分别交各边与点E、H、F、G，则A、E、D、G关于O的对称点分别是 ——、——、——、——
D
G
F
A
B
H
E
C
O
H
F
B
C
做一做：下列哪些图形是中心对称图形？
（１）
（２）
（３）
（４）
１、观察图形，并回答下面的问题：
（１）哪些只是轴对称图形？
（２）哪些只是中心对称图形？
（３）哪些既是轴对称图形，又是中心对称图形？
（１）
（３）
（２）
（４）
（５）
（６）
做一做
例2:已知:如图， ABCD的对角线AC,BD交于点O. 过点O作直线EF，分别交AB，CD于点E，F。 求证：OE=OF
A
B
C
D
F
E
O
EF经过点O，分别交AB、CD于E、F。
解： ∵平行四边形是中心对称图形，O是对称中心
∴点E、F是关于点O的对称点。
∴OE=OF。
轴对称图形
中心对称图形
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折（翻转
180°
）
图形绕中心旋转
180°
3
翻转前后的图形完全重合
旋转前后的图形完全重合
中心对称图形与轴对称图形有什么区别与联系？
4
对应点的连线被对称轴垂直平分
对称中心平分连结两个对称点的线段
通过今天的学习
你有哪些收获？
还存在哪些疑问？
谈谈这节课的收获
中心对称与轴对称有什么区别 又有什么联系
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折1800)后重合 图形绕对称中心旋转1800后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
布置作业:
1、复习、整理、巩固今天所学知识,
2、作业本(1).5.4基础练习必做，希望完成综合运用.
3、课课练B5.4课后作业必做,
当堂训练选做.
4.预习下一节课
具有数学美。因为中心对称图形形状匀称美观。所以许多建筑、工艺品、商标常用这种图形作装饰图案。
平稳旋转。具有中心对称图形形状的物体，能够在所在的平面内绕对称中心平稳旋转。所以在生产中，有关旋转的零部件常设计成中心对称图形。
中心对称的特征与实际应用
名称
图形 中心对称图形 轴对称图形 对称中心，对称轴
线
段
角
等腰三角形
平行四边形
是
是
是
是
不是
不是
不是
是
线段中点
线段的中垂线和线段本身所在的直线
角平分线所在的直线
底边的中垂线
对角线交点
名称
图形
中心对称图形
轴对称图形
对称中心，对称轴
矩形
菱形
正方形
圆
等腰梯形
是
是
是
是
是
是
是
是
是
不是
圆心
边的中垂线
对角线交点
对角线交点
对角线所在直线
对角线交点
对角线所在直线
边的中垂线
直径所在直线
两底的中垂线
你能画一条直线，将以下正方形分成形状大小完全相同的两部分吗
规律：过两个中心对称图形的中心画出一条直线即可
1、你能画一条直线就把下列图形面积等分吗？
方法：首先把棋子摆在对称中心，然后每次都根据对方棋子的位置找出中心对称的位置来摆放，一定能获胜.
2、两人玩摆放棋子游戏，每人轮流把一枚棋子摆放在圆形盘上，依次下去，最后棋子摆不下者为输方。问：要赢此盘棋，应采取什么绝招？
再见！