平行四边形的判定(1)
图片预览


文档简介
(共16张PPT)
B
D
A
C
O
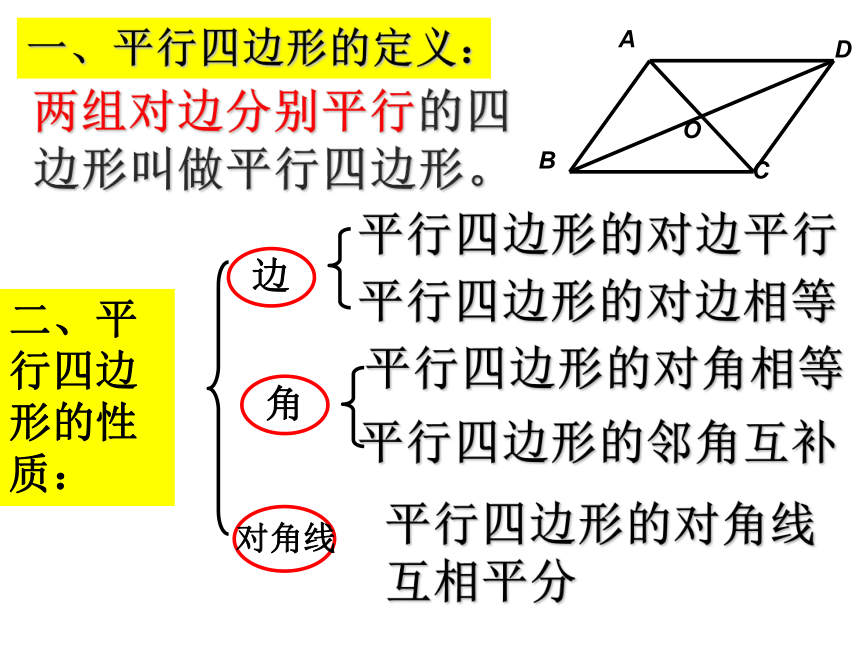
二、平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
一、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形。
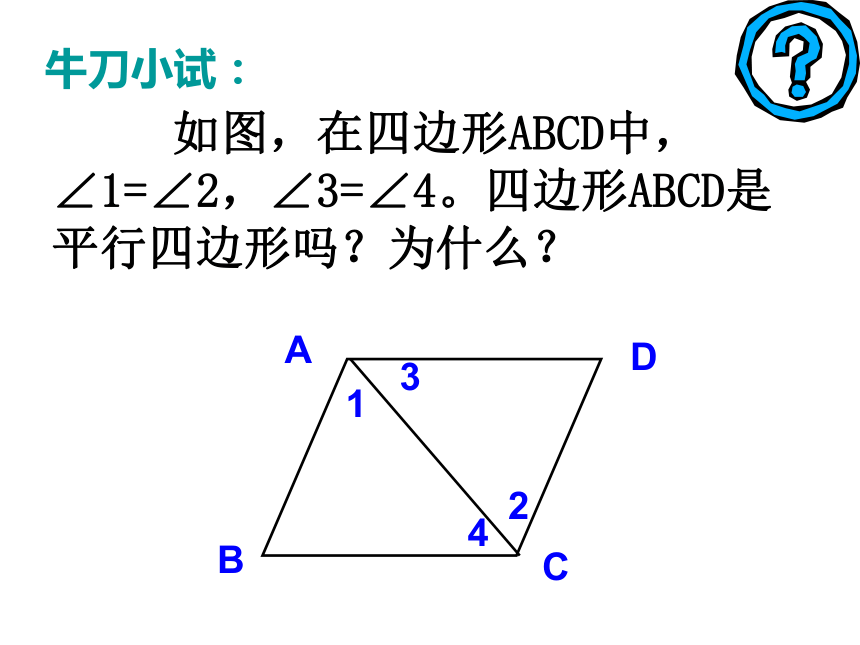
如图,在四边形ABCD中,∠1=∠2,∠3=∠4。四边形ABCD是平行四边形吗?为什么?
牛刀小试:
A
B
C
D
1
2
3
4
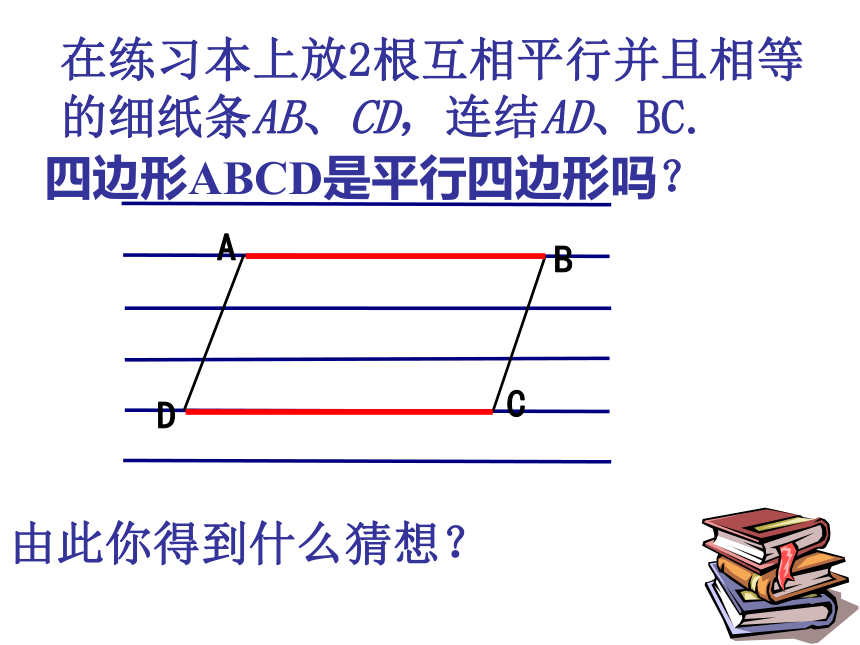
由此你得到什么猜想?
四边形ABCD是平行四边形吗?
A
D
B
C
在练习本上放2根互相平行并且相等的细纸条AB、CD,连结AD、BC.
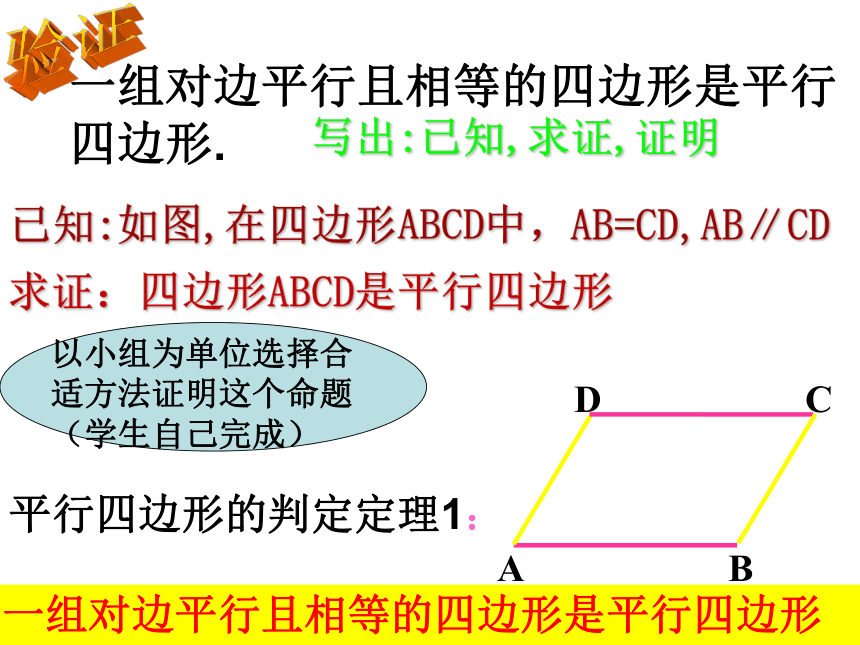
一组对边平行且相等的四边形是平行四边形.
写出:已知,求证,证明
已知:如图,在四边形ABCD中,AB=CD,AB∥CD
求证:四边形ABCD是平行四边形
以小组为单位选择合适方法证明这个命题(学生自己完成)
B
C
A
D
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形
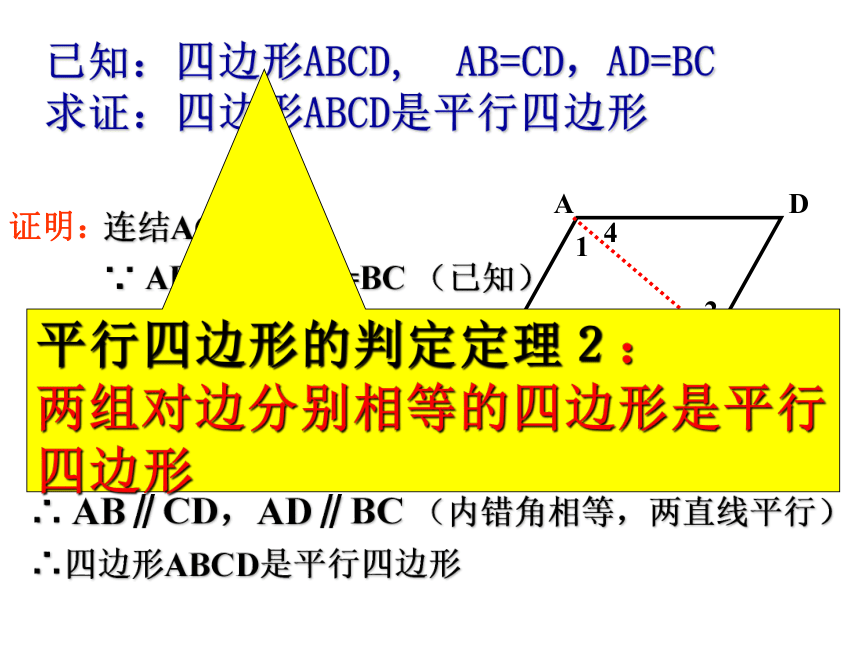
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
B
D
A
C
2
1
3
4
连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
平行四边形的判定定理2:
两组对边分别相等的四边形是平行四边形
1.下列条件中,能判断一个四边形是
平行四边形的是( )
A.一组对边平行
B.一组对边相等
C.一组对边平行且相等
D.一组对边相等,一组对角相等
C
(2009中考)
2.在四边形ABCD中,已知AB=CD,再添加一个
条件 ,(写出一个即可),则四边形
ABCD是平行四边形.(图形中不再添加辅助
线)
A
B
C
D
AD=BC
定理1:一组对边平行且相等的四形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
定义:两组对边分别平行的四边形叫做平行四边形。
3.四边形边长顺次为a,b,c,d,且满足
则此四边形一定是 .
所以这个四边形是平行四边形
平行四边形
由
4:已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图)。求证:EB=DF
5:已知:如图,E,F是 ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
变式:已知:如图,在 ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F。 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
变式:已知:如图,在 ABCD中,E,F是对角线BD上的两点,且BE=DF.M,N分别是AD和BC边上的中点. 求证:四边形ENFM是平行四边形。
A
B
C
D
E
F
M
N
D
A
B
C
E
F
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
6:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
已知直角坐标系内三个点A(-1,-2),B(2,-1),C(-2,1),四边形ABCD是平行四边形则第四个顶点D的坐标
7.合作学习:
小结:平行四边形的判别方法:
图形语言 符号语言
定义
判定
定理1
判定
定理2
判定
定理2
AB∥CD
AD∥BC
AB∥CD
AB=CD
AB=CD
OA=OC
OB=OD
AD=BC
四边形ABCD是平行四边形
四边形ABCD是平行四边形
四边形ABCD是平行四边形
四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
O
D
B
D
A
C
O
二、平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
一、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形。
如图,在四边形ABCD中,∠1=∠2,∠3=∠4。四边形ABCD是平行四边形吗?为什么?
牛刀小试:
A
B
C
D
1
2
3
4
由此你得到什么猜想?
四边形ABCD是平行四边形吗?
A
D
B
C
在练习本上放2根互相平行并且相等的细纸条AB、CD,连结AD、BC.
一组对边平行且相等的四边形是平行四边形.
写出:已知,求证,证明
已知:如图,在四边形ABCD中,AB=CD,AB∥CD
求证:四边形ABCD是平行四边形
以小组为单位选择合适方法证明这个命题(学生自己完成)
B
C
A
D
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
B
D
A
C
2
1
3
4
连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
平行四边形的判定定理2:
两组对边分别相等的四边形是平行四边形
1.下列条件中,能判断一个四边形是
平行四边形的是( )
A.一组对边平行
B.一组对边相等
C.一组对边平行且相等
D.一组对边相等,一组对角相等
C
(2009中考)
2.在四边形ABCD中,已知AB=CD,再添加一个
条件 ,(写出一个即可),则四边形
ABCD是平行四边形.(图形中不再添加辅助
线)
A
B
C
D
AD=BC
定理1:一组对边平行且相等的四形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
定义:两组对边分别平行的四边形叫做平行四边形。
3.四边形边长顺次为a,b,c,d,且满足
则此四边形一定是 .
所以这个四边形是平行四边形
平行四边形
由
4:已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图)。求证:EB=DF
5:已知:如图,E,F是 ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
变式:已知:如图,在 ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F。 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
变式:已知:如图,在 ABCD中,E,F是对角线BD上的两点,且BE=DF.M,N分别是AD和BC边上的中点. 求证:四边形ENFM是平行四边形。
A
B
C
D
E
F
M
N
D
A
B
C
E
F
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
6:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
已知直角坐标系内三个点A(-1,-2),B(2,-1),C(-2,1),四边形ABCD是平行四边形则第四个顶点D的坐标
7.合作学习:
小结:平行四边形的判别方法:
图形语言 符号语言
定义
判定
定理1
判定
定理2
判定
定理2
AB∥CD
AD∥BC
AB∥CD
AB=CD
AB=CD
OA=OC
OB=OD
AD=BC
四边形ABCD是平行四边形
四边形ABCD是平行四边形
四边形ABCD是平行四边形
四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
O
D
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
