6.2.2 反比例函数的图象和性质(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 6.2.2 反比例函数的图象和性质(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 706.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-05 00:00:00 | ||
图片预览




文档简介
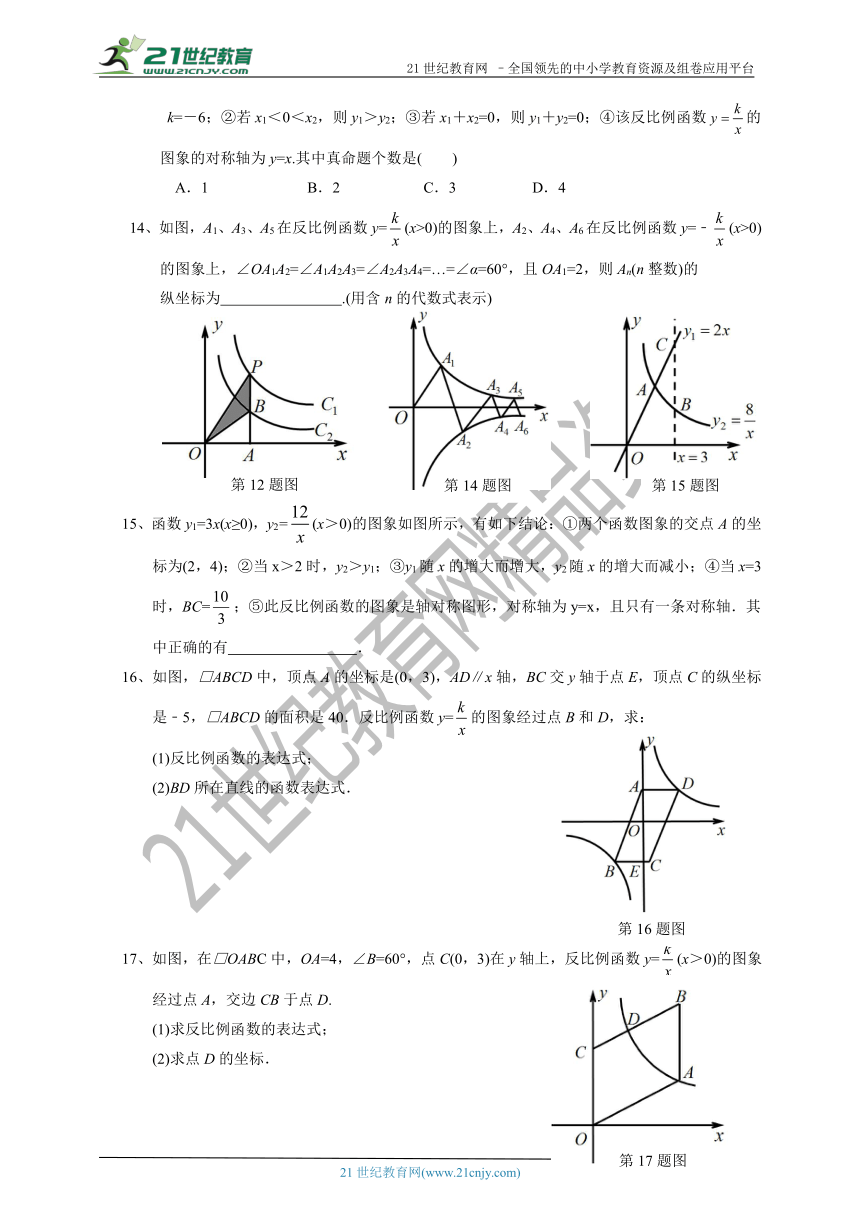
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.2
反比例函数的图象和性质
第2课时
反比例函数的图象和性质(2)
【知识清单】
1.当k>0时,在图象所在的第一、三象限内,函数值y随自变量x的增大而减小;
2.当k<0时,在图象所在的第二、四象限内,函数值y随自变量x的增大而增大.
【经典例题】
例题1、若反比例函数的图象在其象限内,y随着x的增大而增大,则k的取值不可以是( )
A.3
B.4
C.7
D.15
【考点】反比例函数的图象和性质(增减性).
【分析】根据反比例函数性质:在图象所在的第二、四象限内,函数值y随自变量x的增大而增大,则有k<0,即7﹣2m<0,解出m即可.
【解答】根据题意,得7﹣2m<0,
解得m>.
故选A.
【点评】本题主要目的是检查学生对初中反比例函数的性质相关知识的理解,这类是中考的热点.
例题2、已知点(x1,y1)、(x2,y2)、(x3,y3)在双曲线y=﹣上,当x1<0A.
y1B.
y1C.
y3D.
y2【考点】反比例函数的图象和性质和反比例函数图象上点的坐标特征.
【分析】?先根据题意判断出各点所在的象限,再根据函数的增减性即可得出结论.
【解答】∵反比例函数y=﹣中,k=﹣17<0,
∴函数图象的两个分支分别位于二四象限,在每一象限内,y随x的增大而增大.
∵x1<0∴点(x1,y1)位于第二象限,点(x2,y2)、(x3,y3)位于第四象限,
∴y2故选D.
【点评】本题考查的是反比例函数图象上点的坐标特点,图形结合是解决这类问题的关键.
【夯实基础】
1、
下列函数中,函数值y随自变量x的值增大而增大的是(
)
A.y=
B.y=﹣
C.y=
D.y=﹣
2、若点A(﹣3,y1),B(﹣2,y2),C(3,y3)在反比例函数的图像上,则y1,y2,y3的大小关系是(
)
A.y1B.y3C.y2D.y33、正比例函数y=kx与反比例函数y=的图像相交于A,C两点,过点A作x轴的垂线交x轴于
点B,
过点C作x轴的垂线交x轴于点D,连结BC,AD则阴影的面积为(
)
A.12
B.9
C.6
D.3
4、如图,在平面直角坐标系中,矩形ABCD的顶点A,D分别在x轴、和y轴上,对角线DB∥x轴,反比例函数y=(k>0,x>0)的图象经过矩形对角线的交点E,若点A的坐标为(3,0),若点D的坐标为(0,6),则k的值为(
)
A.90
B.
45
C.30
D.22.5
5、已知点A为双曲线y=图象上的点,点O为坐标原点,过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为6,则k的值为
.
6、函数y=x+的图象如图所示,对该函数的性质的论断:①该函数的图象是中心对称图形;②当x>0时,该函数在x=1时取得最小值;③当x>1时,y随x的增大而减小;④y的值不可能为﹣1,其中一定正确的有
.(填写序号)
7、已知一次函数y=﹣4x+8和反比例函数y=(k≠0).
(1)当k满足什么条件时,这两个函数的图像有两个交点;
(2)设这两个函数的公共点为A,B,当∠AOB分别为锐角和钝角时,求k的取值范围.
8、如图,一次函数y=x+3的图象与y轴相交于点A,与反比例函数y=(x>0)的图像相交于
B(m,4),求(1)反比例函数的解析式;(2)若点C在反比例函数y=(x>0)的图像上,且点C与点B关于直线y=x的对称,
求△ABC的面积.
9、如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(a,3)、B两点,BC⊥x轴,垂足为C,△AOC的面积是6.
(1)求m、n的值;
(2)求直线AC的解析式.
【提优特训】
10、已知反比例函数y=,利用反比例函数的增减性,求x≤﹣3时,y的取值范围()
A.?x>﹣4
B.?x<﹣4
C.?0D.
-411、已知点A在函数y1=(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
12、如图,两个反比例函数y=
和y=在第一象限内的图象分别是C1和C2,若点P在C1上,过点P作PA⊥x轴于点A,交C2图象于点B,则△POB的面积为
A.7
B.3?
C.2
D.1
13、已知反比例函数的图象分别位于第二、第四象限,A(x1,y1)、B(x2,y2)两点在该图象上,下列命题:①过点A作AC⊥x轴,C为垂足,连接OA.若△ACO的面积为3,则
k=-6;②若x1<0<x2,则y1>y2;③若x1+x2=0,则y1+y2=0;④该反比例函数的图象的对称轴为y=x.其中真命题个数是(
)
A.1
B.2
C.3
D.4
14、如图,A1、A3、A5在反比例函数y=(x>0)的图象上,A2、A4、A6在反比例函数y=﹣(x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n整数)的
纵坐标为
.(用含n的代数式表示)
15、函数y1=3x(x≥0),y2=(x>0)的图象如图所示,有如下结论:①两个函数图象的交点A的坐标为(2,4);②当x>2时,y2>y1;③y1随x的增大而增大,y2随x的增大而减小;④当x=3时,BC=;⑤此反比例函数的图象是轴对称图形,对称轴为y=x,且只有一条对称轴.其中正确的有
.
16、如图,□ABCD中,顶点A的坐标是(0,3),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是﹣5,□ABCD的面积是40.反比例函数y=的图象经过点B和D,求:
(1)反比例函数的表达式;
(2)BD所在直线的函数表达式.
17、如图,在□OABC中,OA=4,∠B=60°,点C(0,3)在y轴上,反比例函数y=(x>0)的图象经过点A,交边CB于点D.
(1)求反比例函数的表达式;
(2)求点D的坐标.
18、如图,双曲线y=(k为常数,且k≠0)与直线y=﹣2x+b,交于A(﹣m,m﹣2),B(1,n)两点,与直线AB交x轴于点C,交y轴于点D,
(1)求k
、b与m的值;
(2)求证:AC=CD=DB;
(3)点P为CD上的动点,若△POB的面积为S△POB
=,
求点P的坐标.
【中考链接】
19、(2019?遵义)已知反比例函数图象经过点A(1,a),B(3,b),则a,b的关系正确的是(
)
A.a=b
B.a=﹣b
C.aD.a>b
20、(2019?黔东南)若点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3
B.y3>y2>y1
C.y2>y1>y3
D.y1>y3>y2
21、(2019?宿迁)一次函数y=kx+b的图像与反比例函数的图像相交于A(﹣1,m),
B(n,
﹣1)两点?.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)写出一次函数值大于反比例函
数值的x的取值范围.
22、(2019?聊城)
如图,点A(,4),B(3,m)是直线AB与反比例函数y=(x>0)图象的两个
交点,AC⊥x轴,垂足为点C,已知D(0,1),
连接AD,BD,BC.
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2.求S2﹣S1.
参考答案
1、C
2、B
3、C
4、B
5、12或12
6、①②④
10、D
11、A
12、C
13、C
14、
15、①③④⑤
19、D
20、C
7、已知一次函数y=﹣4x+8和反比例函数y=(k≠0).
(1)当k满足什么条件时,这两个函数的图像有两个交点;
(2)设这两个函数的公共点为A,B,当∠AOB分别为锐角和钝角时,求k的取值范围.
解:(1)∵y=﹣4x+8,y=有两个交点,
∴方程有﹣4x+8=有两个不相等的实数根.
∴﹣4x?+8x=k,即4x?﹣8x+k=0,
∵△=(﹣8)?﹣4×4k>0,
∴16k<64,
∴
k<4且k≠0;
(2)若自k<0,则y=在第二和第四象限,所以两个交点分别在第二和第四象限,
所以此时∠AOB是钝角,
若0所以∠AOB是锐角.
8、如图,一次函数y=x+3的图象与y轴相交于点A,与反比例函数y=(x>0)的图像相交于
B(m,4),求(1)反比例函数的解析式;(2)若点C在反比例函数y=(x>0)的图像上,且点C与点B关于直线y=x的对称,
求△ABC的面积.
解:(1)∵一次函数y=x+3的图象经过点B,
∴4=m+3,解m=2,
∴点B的坐标为(2,4).
∵点B(2,4)在在反比例函数y=(x>0)的图象上,
∴k=2×4=8,
∴反比例函数的解析式为y=;
(2)∵且点C与点B关于直线y=x的对称,
∴点C的坐标为(4,2),
设直线OC的解析式为y=ax,
将点C(4,2)的代入y=ax得2=4a,
解得a=,
∴
直线OC的解析式为y=x,
∴AB∥OC,
∴△ABC的面积=△AOB的面积
∵一次函数y=x+3的图象与y轴相交于点A,
∴当x=0时,y=3,即OA=3.
∴△ABC的面积=△AOB的面积=×2AO=×2×3=3.
9、如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(a,3)、B两点,BC⊥x轴,垂足为C,△AOC的面积是6.
(1)求m、n的值;
(2)求直线AC的解析式.
解:(1)∵直线y=mx与双曲线y=相交于A,B两点,
∴点A与点B关于原点中心对称,
∴B(﹣a,﹣3),
∴C(﹣a,0);
∵S△AOC=6,
∴×(﹣a)×3=6,解得a=﹣4,
∴A(-4,3),B(4,
﹣3),
C(4,0)
∵直线y=mx与双曲线y=相交于A(﹣4,3),
∴3=﹣4m,n=﹣4×3=12,
∴m=,
n=12;
(2)设直线AC的解析式为y=kx+b,
把A(﹣2,3),
C(2,0)代入y=kx+b得解得,
∴直线AC的解析式为y=x+.
16、如图,□ABCD中,顶点A的坐标是(0,3),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是﹣5,□ABCD的面积是40.反比例函数y=的图象经过点B和D,求:
(1)反比例函数的表达式;
(2)BD所在直线的函数表达式.
解:(1)∵顶点A的坐标是(0,3),顶点C的纵坐标是﹣5,
∴AE=8,
又□ABCD的面积是40,
∴AD=BC=5,
∴D(5,3)
∴k=5×3=15,
∴反比例函数解析式为y=;
(2)由题意知B的纵坐标为﹣5,
∴其横坐标为﹣3,
∴B(﹣3,﹣5),
设BD所在直线解析式为y=kx+b,
将B(﹣3,﹣5)、D(5,3)代入,得:,
解得:,
所以AB所在直线解析式为y=x﹣2.
17、如图,在□OABC中,OA=4,∠B=60°,点C(0,3)在y轴上,反比例函数y=(x>0)的图象经过点A,交边CB于点D.
(1)求反比例函数的表达式;
(2)求点D的坐标.
解:(1)延长BA交x轴于点E,
∵四边形OABC是平行四边形,∠B=60°,
∴BA∥OC,
∴BA⊥x轴.
∴∠AOC=60°,∠AOE=30°,
在Rt△AOE中,∵OA=4,
∠AOE=30°,
∴AE=2,,OE=2
∴点A的坐标为(2,2
),
∵反比例函数y=(x>0)的图象经过点A,
∴将点A(2,2
)代入y=(x>0),
∴k=2×2=4,
∴反比例函数的表达式为y=(x>0),
(2)∵点C(0,3)在y轴上,
∴OC=AB=3,
∴B的横坐标为2,B的纵坐标为2+3=5
∴点B的坐标为(2,5)
设直线CB的解析式为y=kx+3,
将点B的坐标为(2,5)代入y=kx+3得5=2k+3
解得k=
∴直线CB的解析式为y=x+3,,
解方程组,解得
(舍去).
点D的坐标为(,4).
18、如图,双曲线y=(k为常数,且k≠0)与直线y=﹣2x+b,交于A(﹣m,m﹣2),B(1,n)两点,与直线AB交x轴于点C,交y轴于点D,
(1)求k
、b与m的值;
(2)求证:AC=CD=DB;
(3)点P为CD上的动点,若△POB的面积为S△POB
=,
求点P的坐标.
解:(1)∵点A(﹣m,m﹣2),B(1,n),
在直线y=﹣2x+b上,
∴,解得:,
∴B(1,﹣4),
将B(1,﹣4)代入反比例函数解析式y=,
∴k=﹣4,.
∴反比例函数解析式为y=,
∴直线AB的解析式为y=﹣2x﹣2,
解方程组,得,,
经检验和都是原方程组的解,
∴点A的坐标为(-2,2),
∴﹣m=﹣2,m=4.
∴k=﹣4,b=﹣2,m=4;
(2)过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
∵直线AB的解析式为y=﹣2x﹣2,
令x=0,解得y=﹣2,令y=0,解得x=﹣1,
∴C(﹣1,0),D(0,﹣2),
∴OC=1,OD=2,
∵点A的坐标为(﹣2,2),
点B的坐标为(1,﹣4),
∴AE=2,OE=2,OF=1,BF=4
在△AEC和△DOC
∵
∴AC=DC,EC=OC=1,
在Rt△DOC中,CD===,
在Rt△CFB中,CB===,
∴DB=CB﹣CD=﹣=,
∴CD=
DB
∴AC=DC=
DB;
(3)∵S△BOD
=OD·OF=×2×1=1,△POB的面积为,
∴S△POD=S△POB
﹣S△BOD
=﹣1=,
∵S△COD=OC·OD=×2×1=1,
∴S△COD=S△POD,
∴OP是边CD上的中线,
∴P为CD的中点,
∴P(﹣,﹣1).
21、(2019?宿迁)一次函数y=kx+b的图像与反比例函数的图像相交于A(﹣1,m),
B(n,
﹣1)两点?.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)写出一次函数值大于反比例函
数值的x的取值范围.
解:(1)把A(﹣2,1)代入y=得:m=﹣2,
则反比例函数的解析式是y=﹣;
把B(1,n)代入得n=﹣=﹣2,
则B的坐标是(1,﹣2).
根据题意得:,
解得:,
则函数的解析式是y=﹣x﹣1;
(2)在y=﹣x﹣1中,令x=0,解得y=﹣1,则函数与y轴的交点坐标是(0,﹣1).
则S△AOB=×1×(1+2)=;
(3)当x<﹣2或022、(2019?聊城)
如图,点A(,4),B(3,m)是直线AB与反比例函数y=(x>0)图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2.求S2﹣S1.
解:(1)由点A(,4),B(3,m)在
反比例函数y=(x>0)图象上
∴n=4×=6,
∴反比例函数的解析式为y=(x>0),
将点B(3,m)代入y=(x>0)得m=2
∴B(3,2)
设直线AB的表达式为y=kx+b
∴,解得
∴直线AB的表达式为y=﹣x+6;
(2)由点A、B坐标得AC=4,点B到AC的距离为3﹣=
∴S1=×4×=3
设AB与y轴的交点为E,可得E(0,6),如图:
∴DE=6﹣1=5
由点A(,4),B(3,2)知点A,B到DE的距离分别为,3
∴S2=S△BDE﹣S△ACD=×5×3﹣×5×=,
∴S2﹣S1=﹣3=.
第16题图
第8题图
第22题图
第12题图
第15题图
第18题图
第22题图
第21题图
第5题图
第6题图
第17题图
第17题图
第18题图
第18题图
第16题图
第3题图
第8题图
第14题图
第17题图
第21题图
第9题图
第9题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.2
反比例函数的图象和性质
第2课时
反比例函数的图象和性质(2)
【知识清单】
1.当k>0时,在图象所在的第一、三象限内,函数值y随自变量x的增大而减小;
2.当k<0时,在图象所在的第二、四象限内,函数值y随自变量x的增大而增大.
【经典例题】
例题1、若反比例函数的图象在其象限内,y随着x的增大而增大,则k的取值不可以是( )
A.3
B.4
C.7
D.15
【考点】反比例函数的图象和性质(增减性).
【分析】根据反比例函数性质:在图象所在的第二、四象限内,函数值y随自变量x的增大而增大,则有k<0,即7﹣2m<0,解出m即可.
【解答】根据题意,得7﹣2m<0,
解得m>.
故选A.
【点评】本题主要目的是检查学生对初中反比例函数的性质相关知识的理解,这类是中考的热点.
例题2、已知点(x1,y1)、(x2,y2)、(x3,y3)在双曲线y=﹣上,当x1<0
y1
y1
y3
y2
【分析】?先根据题意判断出各点所在的象限,再根据函数的增减性即可得出结论.
【解答】∵反比例函数y=﹣中,k=﹣17<0,
∴函数图象的两个分支分别位于二四象限,在每一象限内,y随x的增大而增大.
∵x1<0
∴y2
【点评】本题考查的是反比例函数图象上点的坐标特点,图形结合是解决这类问题的关键.
【夯实基础】
1、
下列函数中,函数值y随自变量x的值增大而增大的是(
)
A.y=
B.y=﹣
C.y=
D.y=﹣
2、若点A(﹣3,y1),B(﹣2,y2),C(3,y3)在反比例函数的图像上,则y1,y2,y3的大小关系是(
)
A.y1
点B,
过点C作x轴的垂线交x轴于点D,连结BC,AD则阴影的面积为(
)
A.12
B.9
C.6
D.3
4、如图,在平面直角坐标系中,矩形ABCD的顶点A,D分别在x轴、和y轴上,对角线DB∥x轴,反比例函数y=(k>0,x>0)的图象经过矩形对角线的交点E,若点A的坐标为(3,0),若点D的坐标为(0,6),则k的值为(
)
A.90
B.
45
C.30
D.22.5
5、已知点A为双曲线y=图象上的点,点O为坐标原点,过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为6,则k的值为
.
6、函数y=x+的图象如图所示,对该函数的性质的论断:①该函数的图象是中心对称图形;②当x>0时,该函数在x=1时取得最小值;③当x>1时,y随x的增大而减小;④y的值不可能为﹣1,其中一定正确的有
.(填写序号)
7、已知一次函数y=﹣4x+8和反比例函数y=(k≠0).
(1)当k满足什么条件时,这两个函数的图像有两个交点;
(2)设这两个函数的公共点为A,B,当∠AOB分别为锐角和钝角时,求k的取值范围.
8、如图,一次函数y=x+3的图象与y轴相交于点A,与反比例函数y=(x>0)的图像相交于
B(m,4),求(1)反比例函数的解析式;(2)若点C在反比例函数y=(x>0)的图像上,且点C与点B关于直线y=x的对称,
求△ABC的面积.
9、如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(a,3)、B两点,BC⊥x轴,垂足为C,△AOC的面积是6.
(1)求m、n的值;
(2)求直线AC的解析式.
【提优特训】
10、已知反比例函数y=,利用反比例函数的增减性,求x≤﹣3时,y的取值范围()
A.?x>﹣4
B.?x<﹣4
C.?0
-4
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
12、如图,两个反比例函数y=
和y=在第一象限内的图象分别是C1和C2,若点P在C1上,过点P作PA⊥x轴于点A,交C2图象于点B,则△POB的面积为
A.7
B.3?
C.2
D.1
13、已知反比例函数的图象分别位于第二、第四象限,A(x1,y1)、B(x2,y2)两点在该图象上,下列命题:①过点A作AC⊥x轴,C为垂足,连接OA.若△ACO的面积为3,则
k=-6;②若x1<0<x2,则y1>y2;③若x1+x2=0,则y1+y2=0;④该反比例函数的图象的对称轴为y=x.其中真命题个数是(
)
A.1
B.2
C.3
D.4
14、如图,A1、A3、A5在反比例函数y=(x>0)的图象上,A2、A4、A6在反比例函数y=﹣(x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n整数)的
纵坐标为
.(用含n的代数式表示)
15、函数y1=3x(x≥0),y2=(x>0)的图象如图所示,有如下结论:①两个函数图象的交点A的坐标为(2,4);②当x>2时,y2>y1;③y1随x的增大而增大,y2随x的增大而减小;④当x=3时,BC=;⑤此反比例函数的图象是轴对称图形,对称轴为y=x,且只有一条对称轴.其中正确的有
.
16、如图,□ABCD中,顶点A的坐标是(0,3),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是﹣5,□ABCD的面积是40.反比例函数y=的图象经过点B和D,求:
(1)反比例函数的表达式;
(2)BD所在直线的函数表达式.
17、如图,在□OABC中,OA=4,∠B=60°,点C(0,3)在y轴上,反比例函数y=(x>0)的图象经过点A,交边CB于点D.
(1)求反比例函数的表达式;
(2)求点D的坐标.
18、如图,双曲线y=(k为常数,且k≠0)与直线y=﹣2x+b,交于A(﹣m,m﹣2),B(1,n)两点,与直线AB交x轴于点C,交y轴于点D,
(1)求k
、b与m的值;
(2)求证:AC=CD=DB;
(3)点P为CD上的动点,若△POB的面积为S△POB
=,
求点P的坐标.
【中考链接】
19、(2019?遵义)已知反比例函数图象经过点A(1,a),B(3,b),则a,b的关系正确的是(
)
A.a=b
B.a=﹣b
C.a
20、(2019?黔东南)若点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3
B.y3>y2>y1
C.y2>y1>y3
D.y1>y3>y2
21、(2019?宿迁)一次函数y=kx+b的图像与反比例函数的图像相交于A(﹣1,m),
B(n,
﹣1)两点?.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)写出一次函数值大于反比例函
数值的x的取值范围.
22、(2019?聊城)
如图,点A(,4),B(3,m)是直线AB与反比例函数y=(x>0)图象的两个
交点,AC⊥x轴,垂足为点C,已知D(0,1),
连接AD,BD,BC.
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2.求S2﹣S1.
参考答案
1、C
2、B
3、C
4、B
5、12或12
6、①②④
10、D
11、A
12、C
13、C
14、
15、①③④⑤
19、D
20、C
7、已知一次函数y=﹣4x+8和反比例函数y=(k≠0).
(1)当k满足什么条件时,这两个函数的图像有两个交点;
(2)设这两个函数的公共点为A,B,当∠AOB分别为锐角和钝角时,求k的取值范围.
解:(1)∵y=﹣4x+8,y=有两个交点,
∴方程有﹣4x+8=有两个不相等的实数根.
∴﹣4x?+8x=k,即4x?﹣8x+k=0,
∵△=(﹣8)?﹣4×4k>0,
∴16k<64,
∴
k<4且k≠0;
(2)若自k<0,则y=在第二和第四象限,所以两个交点分别在第二和第四象限,
所以此时∠AOB是钝角,
若0
8、如图,一次函数y=x+3的图象与y轴相交于点A,与反比例函数y=(x>0)的图像相交于
B(m,4),求(1)反比例函数的解析式;(2)若点C在反比例函数y=(x>0)的图像上,且点C与点B关于直线y=x的对称,
求△ABC的面积.
解:(1)∵一次函数y=x+3的图象经过点B,
∴4=m+3,解m=2,
∴点B的坐标为(2,4).
∵点B(2,4)在在反比例函数y=(x>0)的图象上,
∴k=2×4=8,
∴反比例函数的解析式为y=;
(2)∵且点C与点B关于直线y=x的对称,
∴点C的坐标为(4,2),
设直线OC的解析式为y=ax,
将点C(4,2)的代入y=ax得2=4a,
解得a=,
∴
直线OC的解析式为y=x,
∴AB∥OC,
∴△ABC的面积=△AOB的面积
∵一次函数y=x+3的图象与y轴相交于点A,
∴当x=0时,y=3,即OA=3.
∴△ABC的面积=△AOB的面积=×2AO=×2×3=3.
9、如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(a,3)、B两点,BC⊥x轴,垂足为C,△AOC的面积是6.
(1)求m、n的值;
(2)求直线AC的解析式.
解:(1)∵直线y=mx与双曲线y=相交于A,B两点,
∴点A与点B关于原点中心对称,
∴B(﹣a,﹣3),
∴C(﹣a,0);
∵S△AOC=6,
∴×(﹣a)×3=6,解得a=﹣4,
∴A(-4,3),B(4,
﹣3),
C(4,0)
∵直线y=mx与双曲线y=相交于A(﹣4,3),
∴3=﹣4m,n=﹣4×3=12,
∴m=,
n=12;
(2)设直线AC的解析式为y=kx+b,
把A(﹣2,3),
C(2,0)代入y=kx+b得解得,
∴直线AC的解析式为y=x+.
16、如图,□ABCD中,顶点A的坐标是(0,3),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是﹣5,□ABCD的面积是40.反比例函数y=的图象经过点B和D,求:
(1)反比例函数的表达式;
(2)BD所在直线的函数表达式.
解:(1)∵顶点A的坐标是(0,3),顶点C的纵坐标是﹣5,
∴AE=8,
又□ABCD的面积是40,
∴AD=BC=5,
∴D(5,3)
∴k=5×3=15,
∴反比例函数解析式为y=;
(2)由题意知B的纵坐标为﹣5,
∴其横坐标为﹣3,
∴B(﹣3,﹣5),
设BD所在直线解析式为y=kx+b,
将B(﹣3,﹣5)、D(5,3)代入,得:,
解得:,
所以AB所在直线解析式为y=x﹣2.
17、如图,在□OABC中,OA=4,∠B=60°,点C(0,3)在y轴上,反比例函数y=(x>0)的图象经过点A,交边CB于点D.
(1)求反比例函数的表达式;
(2)求点D的坐标.
解:(1)延长BA交x轴于点E,
∵四边形OABC是平行四边形,∠B=60°,
∴BA∥OC,
∴BA⊥x轴.
∴∠AOC=60°,∠AOE=30°,
在Rt△AOE中,∵OA=4,
∠AOE=30°,
∴AE=2,,OE=2
∴点A的坐标为(2,2
),
∵反比例函数y=(x>0)的图象经过点A,
∴将点A(2,2
)代入y=(x>0),
∴k=2×2=4,
∴反比例函数的表达式为y=(x>0),
(2)∵点C(0,3)在y轴上,
∴OC=AB=3,
∴B的横坐标为2,B的纵坐标为2+3=5
∴点B的坐标为(2,5)
设直线CB的解析式为y=kx+3,
将点B的坐标为(2,5)代入y=kx+3得5=2k+3
解得k=
∴直线CB的解析式为y=x+3,,
解方程组,解得
(舍去).
点D的坐标为(,4).
18、如图,双曲线y=(k为常数,且k≠0)与直线y=﹣2x+b,交于A(﹣m,m﹣2),B(1,n)两点,与直线AB交x轴于点C,交y轴于点D,
(1)求k
、b与m的值;
(2)求证:AC=CD=DB;
(3)点P为CD上的动点,若△POB的面积为S△POB
=,
求点P的坐标.
解:(1)∵点A(﹣m,m﹣2),B(1,n),
在直线y=﹣2x+b上,
∴,解得:,
∴B(1,﹣4),
将B(1,﹣4)代入反比例函数解析式y=,
∴k=﹣4,.
∴反比例函数解析式为y=,
∴直线AB的解析式为y=﹣2x﹣2,
解方程组,得,,
经检验和都是原方程组的解,
∴点A的坐标为(-2,2),
∴﹣m=﹣2,m=4.
∴k=﹣4,b=﹣2,m=4;
(2)过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
∵直线AB的解析式为y=﹣2x﹣2,
令x=0,解得y=﹣2,令y=0,解得x=﹣1,
∴C(﹣1,0),D(0,﹣2),
∴OC=1,OD=2,
∵点A的坐标为(﹣2,2),
点B的坐标为(1,﹣4),
∴AE=2,OE=2,OF=1,BF=4
在△AEC和△DOC
∵
∴AC=DC,EC=OC=1,
在Rt△DOC中,CD===,
在Rt△CFB中,CB===,
∴DB=CB﹣CD=﹣=,
∴CD=
DB
∴AC=DC=
DB;
(3)∵S△BOD
=OD·OF=×2×1=1,△POB的面积为,
∴S△POD=S△POB
﹣S△BOD
=﹣1=,
∵S△COD=OC·OD=×2×1=1,
∴S△COD=S△POD,
∴OP是边CD上的中线,
∴P为CD的中点,
∴P(﹣,﹣1).
21、(2019?宿迁)一次函数y=kx+b的图像与反比例函数的图像相交于A(﹣1,m),
B(n,
﹣1)两点?.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)写出一次函数值大于反比例函
数值的x的取值范围.
解:(1)把A(﹣2,1)代入y=得:m=﹣2,
则反比例函数的解析式是y=﹣;
把B(1,n)代入得n=﹣=﹣2,
则B的坐标是(1,﹣2).
根据题意得:,
解得:,
则函数的解析式是y=﹣x﹣1;
(2)在y=﹣x﹣1中,令x=0,解得y=﹣1,则函数与y轴的交点坐标是(0,﹣1).
则S△AOB=×1×(1+2)=;
(3)当x<﹣2或0
如图,点A(,4),B(3,m)是直线AB与反比例函数y=(x>0)图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2.求S2﹣S1.
解:(1)由点A(,4),B(3,m)在
反比例函数y=(x>0)图象上
∴n=4×=6,
∴反比例函数的解析式为y=(x>0),
将点B(3,m)代入y=(x>0)得m=2
∴B(3,2)
设直线AB的表达式为y=kx+b
∴,解得
∴直线AB的表达式为y=﹣x+6;
(2)由点A、B坐标得AC=4,点B到AC的距离为3﹣=
∴S1=×4×=3
设AB与y轴的交点为E,可得E(0,6),如图:
∴DE=6﹣1=5
由点A(,4),B(3,2)知点A,B到DE的距离分别为,3
∴S2=S△BDE﹣S△ACD=×5×3﹣×5×=,
∴S2﹣S1=﹣3=.
第16题图
第8题图
第22题图
第12题图
第15题图
第18题图
第22题图
第21题图
第5题图
第6题图
第17题图
第17题图
第18题图
第18题图
第16题图
第3题图
第8题图
第14题图
第17题图
第21题图
第9题图
第9题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
