浙教版九年级数学上册 第4章 相似三角形达标测试卷 含答案
文档属性
| 名称 | 浙教版九年级数学上册 第4章 相似三角形达标测试卷 含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 312.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 19:02:55 | ||
图片预览




文档简介
第4章达标测试卷
一、选择题(每题3分,共30分)
1.若=,则等于( )
A.
B.
C.
D.
2.若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
A.1:4
B.1:2
C.2:1
D.4:1
3.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=( )
A.2
B.3
C.4
D.5
4.已知△ABC∽△A′B′C′,AB=8,A′B′=6,则=( )
A.2
B.
C.3
D.
5.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,以下说法中错误的是( )
A.△ABC∽△A′B′C′
B.点C、点O、点C′在同一直线上
C.AO:AA′=1:2
D.AB∥A′B′
6.如图,为估算某河的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于( )
A.60
m
B.40
m
C.30
m
D.20
m
7.如图,小正方形的边长均为1,则下列选项中的三角形与△ABC相似的是( )
8.如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF等于( )
A.2
B.2.4
C.2.5
D.2.25
9.如图,在△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,则点F到BC的距离为( )
A.1
B.2
C.12-6
D.6-6
10.如图,在钝角三角形ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分
∠AEB交AB于点M,取BC的中点D,AC的中点N,连结DN,DE,DF.下列结论:①EM=DN;②S△CND=S四边形ABDN;③DE=DF;④DE⊥DF.其中正确结论的个数为( )
A.1
B.2
C.3
D.4
二、填空题(每题3分,共24分)
11.已知=,则=________.
12.如图,在△ABC中,若DE∥BC,AD=2,BD=4,DE=1.5,则BC的长为__________.
13.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形的面积,S2表示长为AD(AD=AB)、宽为AC的矩形的面积,则S1与S2的大小关系为________.
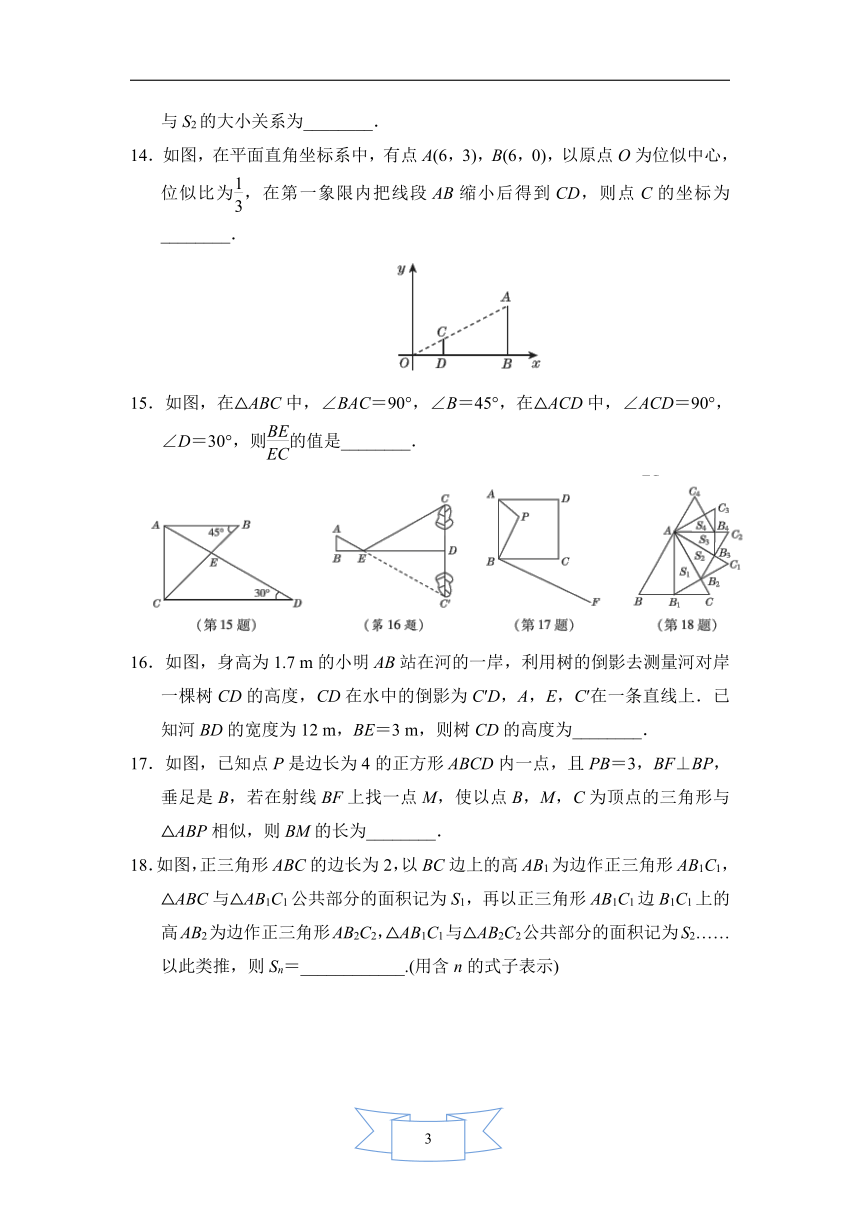
14.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,位似比为,在第一象限内把线段AB缩小后得到CD,则点C的坐标为________.
15.如图,在△ABC中,∠BAC=90°,∠B=45°,在△ACD中,∠ACD=90°,∠D=30°,则的值是________.
16.如图,身高为1.7
m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条直线上.已知河BD的宽度为12
m,BE=3
m,则树CD的高度为________.
17.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,则BM的长为________.
18.如图,正三角形ABC的边长为2,以BC边上的高AB1为边作正三角形AB1C1,△ABC与△AB1C1公共部分的面积记为S1,再以正三角形AB1C1边B1C1上的高AB2为边作正三角形AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2……以此类推,则Sn=____________.(用含n的式子表示)
三、解答题(19,21题每题8分,24题14分,其余每题12分,共66分)
19.如图,四边形ABCD∽四边形EFGH,试求出x及α的大小.
20.如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比.(不写解答过程,直接写出结果)
21.如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
22.如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两个景观灯的间隔都是10
m,在与河岸DE的距离为16
m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的这两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.
23.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
24.如图,E,F分别是正方形ABCD的边DC,CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连结DF.
(1)求证:△ADE≌△DCF.
(2)若E是CD的中点,求证:Q为CF的中点.
(3)连结AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.
答案
一、1.D 2.B 3.C 4.B 5.C
6.B 点拨:∵AB⊥BC,CD⊥BC,
∴∠ABC=∠DCE=90°.
又∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.∴AB=40
m.
7.A 8.B
9.D 点拨:如图,过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H.∵AB=AC,AD=AG,
∴AD∶AB=AG∶AC.
又∵∠BAC=∠DAG,∴△ADG∽△ABC.
∴∠ADG=∠B.∴DG∥BC.
∴AN⊥DG.
∵四边形DEFG是正方形,
∴FG⊥DG.∴FH⊥BC.
∵AB=AC=18,BC=12,
∴BM=BC=6.
∴AM==12.
∵=,即=,
∴AN=6.∴MN=AM-AN=6.
易得四边形GHMN为矩形,
∴GH=MN=6
.
∴FH=GH-GF=6
-6.故选D.
10.D 点拨:∵△ABE是等腰直角三角形,EM平分∠AEB,∴EM是AB边上的中线.∴EM=AB.
∵点D,点N分别是BC,AC的中点,
∴DN是△ABC的中位线.∴DN=AB,DN∥AB.∴EM=DN.①正确.
∵DN∥AB,∴△CDN∽△CBA.
∴==.
∴S△CND=S四边形ABDN.②正确.
如图,连结DM,FN,则DM是△ABC的中位线,∴DM=AC,DM∥AC.
∴四边形AMDN是平行四边形.
∴∠AMD=∠AND.
易知∠ANF=90°,∠AME=90°,
∴∠EMD=∠DNF.
∵FN是AC边上的中线,
∴FN=AC.∴DM=FN.
又∵EM=DN,
∴△DEM≌△FDN.
∴DE=DF,∠FDN=∠DEM.③正确.
∵∠MDN+∠AMD=180°,
∴∠EDF=∠MDN-(∠EDM+∠FDN)=180°-∠AMD-(∠EDM+∠DEM)=180°-(∠AMD+∠EDM+∠DEM)=180°-(180°-∠AME)=180°-(180°-90°)=90°.
∴DE⊥DF.④正确.故选D.
二、11. 点拨:∵=,
∴设a=13x,b=7x,
则==.
12.4.5
13.S1=S2
14.(2,1)
15.
16.5.1
m 17.或3
18.× 点拨:在正三角形ABC中,AB1⊥BC,
∴BB1=BC=1.
在Rt△ABB1中,AB1===,
根据题意可得△AB2B1∽△AB1B,
记△AB1B的面积为S,
∴=.
∴S1=S.同理可得S2=S1,
S3=S2,S4=S3,….
又∵S=×1×=,
∴S1=S=×,
S2=S1=×,
S3=S2=×,
S4=S3=×,…,
Sn=×.
三、19.解:因为四边形ABCD∽四边形EFGH,所以∠H=∠D=95°,则α=360°-95°-118°-67°=80°.再由x∶7=12∶6,解得x=14.
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)S△A1B1C1∶S△A2B2C2=1∶4.
21.(1)证明:∵AB∥FC,∴∠A=∠ECF.
又∵∠AED=∠CEF,且DE=FE,
∴△ADE≌△CFE.
(2)解:方法一:∵AB∥FC,
∴△GBD∽△GCF.∴=.
∴=.∴CF=3.
由(1)得△ADE≌△CFE,
∴AD=CF=3,
∴AB=AD+BD=3+1=4.
方法二:如图,取BC的中点H,连结EH.∵△ADE≌△CFE,
∴AE=CE.∴EH是△ABC的中位线.
∴EH∥AB,且EH=AB.
∴△GBD∽△GHE.
∴=.∴=.
∴EH=2.∴AB=2EH=4.
22.解:由题意可得DE∥BC,
所以△ADE∽△ABC.
所以=,即=.
因为AD=16
m,BC=50
m,DE=20
m,
所以=.
所以DB=24
m.
所以这条河的宽度为24
m.
23.解:(1)由题意可知BE=2t,CF=4t,CE=12-2t.
因为△CEF是等腰直角三角形,∠ECF是直角,所以CE=CF.
所以12-2t=4t,解得t=2.
所以当t=2时,△CEF是等腰直角三角形.
(2)根据题意,可分为两种情况:
①若△EFC∽△ACD,则=,
所以=,解得t=3,
即当t=3时,△EFC∽△ACD.
②若△FEC∽△ACD,则=,
所以=,解得t=1.2,
即当t=1.2时,△FEC∽△ACD.
因此,当t为3或1.2时,以点E,C,F为顶点的三角形与△ACD相似.
24.(1)证明:因为AD=DC,
∠ADE=∠DCF=90°,DE=CF,
所以△ADE≌△DCF.
(2)证明:因为四边形AEHG是正方形,所以∠AEH=90°.
所以∠QEC+∠AED=90°.
又因为∠AED+∠EAD=90°,
所以∠QEC=∠EAD.
因为∠C=∠ADE=90°,
所以△ECQ∽△ADE.所以=.
因为E是CD的中点,所以EC=DE=CD=AD.所以=.
因为DE=CF,所以==.
即Q是CF的中点.
(3)解:S1+S2=S3成立.
理由如下:因为△ECQ∽△ADE,
所以=.所以=.
因为∠C=∠AEQ=90°,
所以△ECQ∽△AEQ.
所以△AEQ∽△ECQ∽△ADE.
所以=,=.
所以+=+=.
在Rt△AEQ中,由勾股定理,得EQ2+AE2=AQ2,
所以+=1,即S1+S2=S3.
一、选择题(每题3分,共30分)
1.若=,则等于( )
A.
B.
C.
D.
2.若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
A.1:4
B.1:2
C.2:1
D.4:1
3.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=( )
A.2
B.3
C.4
D.5
4.已知△ABC∽△A′B′C′,AB=8,A′B′=6,则=( )
A.2
B.
C.3
D.
5.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,以下说法中错误的是( )
A.△ABC∽△A′B′C′
B.点C、点O、点C′在同一直线上
C.AO:AA′=1:2
D.AB∥A′B′
6.如图,为估算某河的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于( )
A.60
m
B.40
m
C.30
m
D.20
m
7.如图,小正方形的边长均为1,则下列选项中的三角形与△ABC相似的是( )
8.如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF等于( )
A.2
B.2.4
C.2.5
D.2.25
9.如图,在△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,则点F到BC的距离为( )
A.1
B.2
C.12-6
D.6-6
10.如图,在钝角三角形ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分
∠AEB交AB于点M,取BC的中点D,AC的中点N,连结DN,DE,DF.下列结论:①EM=DN;②S△CND=S四边形ABDN;③DE=DF;④DE⊥DF.其中正确结论的个数为( )
A.1
B.2
C.3
D.4
二、填空题(每题3分,共24分)
11.已知=,则=________.
12.如图,在△ABC中,若DE∥BC,AD=2,BD=4,DE=1.5,则BC的长为__________.
13.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形的面积,S2表示长为AD(AD=AB)、宽为AC的矩形的面积,则S1与S2的大小关系为________.
14.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,位似比为,在第一象限内把线段AB缩小后得到CD,则点C的坐标为________.
15.如图,在△ABC中,∠BAC=90°,∠B=45°,在△ACD中,∠ACD=90°,∠D=30°,则的值是________.
16.如图,身高为1.7
m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条直线上.已知河BD的宽度为12
m,BE=3
m,则树CD的高度为________.
17.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,则BM的长为________.
18.如图,正三角形ABC的边长为2,以BC边上的高AB1为边作正三角形AB1C1,△ABC与△AB1C1公共部分的面积记为S1,再以正三角形AB1C1边B1C1上的高AB2为边作正三角形AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2……以此类推,则Sn=____________.(用含n的式子表示)
三、解答题(19,21题每题8分,24题14分,其余每题12分,共66分)
19.如图,四边形ABCD∽四边形EFGH,试求出x及α的大小.
20.如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比.(不写解答过程,直接写出结果)
21.如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
22.如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两个景观灯的间隔都是10
m,在与河岸DE的距离为16
m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的这两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.
23.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
24.如图,E,F分别是正方形ABCD的边DC,CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连结DF.
(1)求证:△ADE≌△DCF.
(2)若E是CD的中点,求证:Q为CF的中点.
(3)连结AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.
答案
一、1.D 2.B 3.C 4.B 5.C
6.B 点拨:∵AB⊥BC,CD⊥BC,
∴∠ABC=∠DCE=90°.
又∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.∴AB=40
m.
7.A 8.B
9.D 点拨:如图,过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H.∵AB=AC,AD=AG,
∴AD∶AB=AG∶AC.
又∵∠BAC=∠DAG,∴△ADG∽△ABC.
∴∠ADG=∠B.∴DG∥BC.
∴AN⊥DG.
∵四边形DEFG是正方形,
∴FG⊥DG.∴FH⊥BC.
∵AB=AC=18,BC=12,
∴BM=BC=6.
∴AM==12.
∵=,即=,
∴AN=6.∴MN=AM-AN=6.
易得四边形GHMN为矩形,
∴GH=MN=6
.
∴FH=GH-GF=6
-6.故选D.
10.D 点拨:∵△ABE是等腰直角三角形,EM平分∠AEB,∴EM是AB边上的中线.∴EM=AB.
∵点D,点N分别是BC,AC的中点,
∴DN是△ABC的中位线.∴DN=AB,DN∥AB.∴EM=DN.①正确.
∵DN∥AB,∴△CDN∽△CBA.
∴==.
∴S△CND=S四边形ABDN.②正确.
如图,连结DM,FN,则DM是△ABC的中位线,∴DM=AC,DM∥AC.
∴四边形AMDN是平行四边形.
∴∠AMD=∠AND.
易知∠ANF=90°,∠AME=90°,
∴∠EMD=∠DNF.
∵FN是AC边上的中线,
∴FN=AC.∴DM=FN.
又∵EM=DN,
∴△DEM≌△FDN.
∴DE=DF,∠FDN=∠DEM.③正确.
∵∠MDN+∠AMD=180°,
∴∠EDF=∠MDN-(∠EDM+∠FDN)=180°-∠AMD-(∠EDM+∠DEM)=180°-(∠AMD+∠EDM+∠DEM)=180°-(180°-∠AME)=180°-(180°-90°)=90°.
∴DE⊥DF.④正确.故选D.
二、11. 点拨:∵=,
∴设a=13x,b=7x,
则==.
12.4.5
13.S1=S2
14.(2,1)
15.
16.5.1
m 17.或3
18.× 点拨:在正三角形ABC中,AB1⊥BC,
∴BB1=BC=1.
在Rt△ABB1中,AB1===,
根据题意可得△AB2B1∽△AB1B,
记△AB1B的面积为S,
∴=.
∴S1=S.同理可得S2=S1,
S3=S2,S4=S3,….
又∵S=×1×=,
∴S1=S=×,
S2=S1=×,
S3=S2=×,
S4=S3=×,…,
Sn=×.
三、19.解:因为四边形ABCD∽四边形EFGH,所以∠H=∠D=95°,则α=360°-95°-118°-67°=80°.再由x∶7=12∶6,解得x=14.
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)S△A1B1C1∶S△A2B2C2=1∶4.
21.(1)证明:∵AB∥FC,∴∠A=∠ECF.
又∵∠AED=∠CEF,且DE=FE,
∴△ADE≌△CFE.
(2)解:方法一:∵AB∥FC,
∴△GBD∽△GCF.∴=.
∴=.∴CF=3.
由(1)得△ADE≌△CFE,
∴AD=CF=3,
∴AB=AD+BD=3+1=4.
方法二:如图,取BC的中点H,连结EH.∵△ADE≌△CFE,
∴AE=CE.∴EH是△ABC的中位线.
∴EH∥AB,且EH=AB.
∴△GBD∽△GHE.
∴=.∴=.
∴EH=2.∴AB=2EH=4.
22.解:由题意可得DE∥BC,
所以△ADE∽△ABC.
所以=,即=.
因为AD=16
m,BC=50
m,DE=20
m,
所以=.
所以DB=24
m.
所以这条河的宽度为24
m.
23.解:(1)由题意可知BE=2t,CF=4t,CE=12-2t.
因为△CEF是等腰直角三角形,∠ECF是直角,所以CE=CF.
所以12-2t=4t,解得t=2.
所以当t=2时,△CEF是等腰直角三角形.
(2)根据题意,可分为两种情况:
①若△EFC∽△ACD,则=,
所以=,解得t=3,
即当t=3时,△EFC∽△ACD.
②若△FEC∽△ACD,则=,
所以=,解得t=1.2,
即当t=1.2时,△FEC∽△ACD.
因此,当t为3或1.2时,以点E,C,F为顶点的三角形与△ACD相似.
24.(1)证明:因为AD=DC,
∠ADE=∠DCF=90°,DE=CF,
所以△ADE≌△DCF.
(2)证明:因为四边形AEHG是正方形,所以∠AEH=90°.
所以∠QEC+∠AED=90°.
又因为∠AED+∠EAD=90°,
所以∠QEC=∠EAD.
因为∠C=∠ADE=90°,
所以△ECQ∽△ADE.所以=.
因为E是CD的中点,所以EC=DE=CD=AD.所以=.
因为DE=CF,所以==.
即Q是CF的中点.
(3)解:S1+S2=S3成立.
理由如下:因为△ECQ∽△ADE,
所以=.所以=.
因为∠C=∠AEQ=90°,
所以△ECQ∽△AEQ.
所以△AEQ∽△ECQ∽△ADE.
所以=,=.
所以+=+=.
在Rt△AEQ中,由勾股定理,得EQ2+AE2=AQ2,
所以+=1,即S1+S2=S3.
同课章节目录
