浙教版数学九年级上册第3章 圆的基本性质 达标测试卷(含答案)
文档属性
| 名称 | 浙教版数学九年级上册第3章 圆的基本性质 达标测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 19:05:09 | ||
图片预览


文档简介
第3章达标测试卷
一、选择题(每题3分,共30分)
1.如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )
A.15°
B.60°
C.45°
D.75°
2.如图,已知AB和CD是⊙O的两条直径,连结AD,BC,则α和β的关系是( )
A.α=β
B.β>2α
C.β<2α
D.β=2α
3.如图,要拧开一个边长为6
mm的正六边形螺帽,扳手张开的开口a至少为( )
A.6
mm
B.12
mm
C.6
mm
D.4
mm
4.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B
5.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )
A.60°
B.50°
C.40°
D.20°
6.点A,B,C,D分别是⊙O上不同的四点,∠ABC=65°,则∠ADC=( )
A.65°
B.115°
C.25°
D.65°或115°
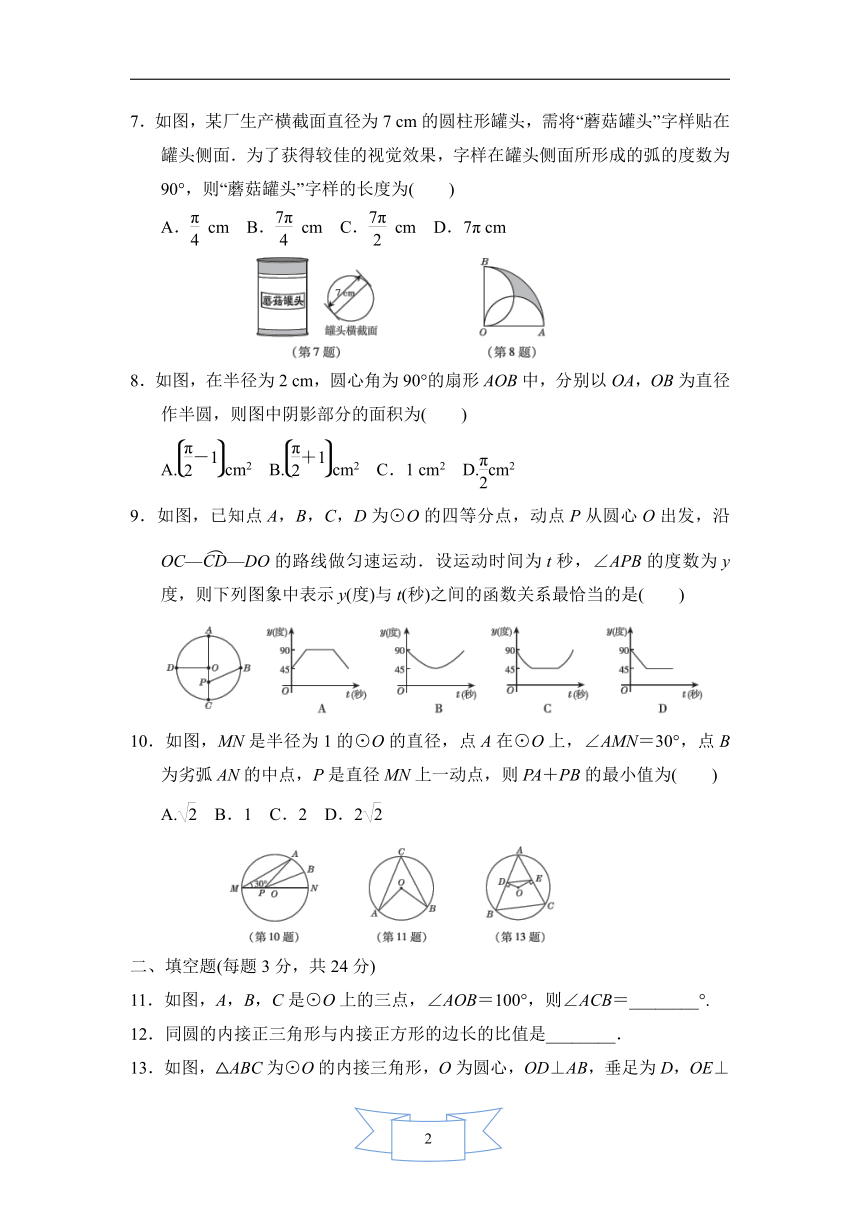
7.如图,某厂生产横截面直径为7
cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳的视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )
A.
cm
B.
cm
C.
cm
D.7π
cm
8.如图,在半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
A.cm2
B.cm2
C.1
cm2
D.cm2
9.如图,已知点A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿OC——DO的路线做匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y(度)与t(秒)之间的函数关系最恰当的是( )
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A.
B.1
C.2
D.2
二、填空题(每题3分,共24分)
11.如图,A,B,C是⊙O上的三点,∠AOB=100°,则∠ACB=________°.
12.同圆的内接正三角形与内接正方形的边长的比值是________.
13.如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E.若DE=3,则BC=________.
14.如图,△ABC是等边三角形,以BC为直径作圆O分别交AB,AC于点D,E,若BC=1,则DC=__________.
15.如图,已知⊙O的直径CD垂直于弦AB,垂足为E,∠AOD=45°,若CD=6
cm,则AB的长为________.
16.如图,将放置于平面直角坐标系中的三角尺AOB绕点O顺时针旋转90°得到△A′OB′.已知∠AOB=30°,∠B=90°,AB=1,则点B′的坐标是__________.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,分别以AC,BC为直径作半圆,则图中阴影部分的面积为________.
18.半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连结OB,OC,延长CO交弦AB于点D,若△OBD是直角三角形,则弦BC的长为____________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径.求证:∠BAM=∠CAP.
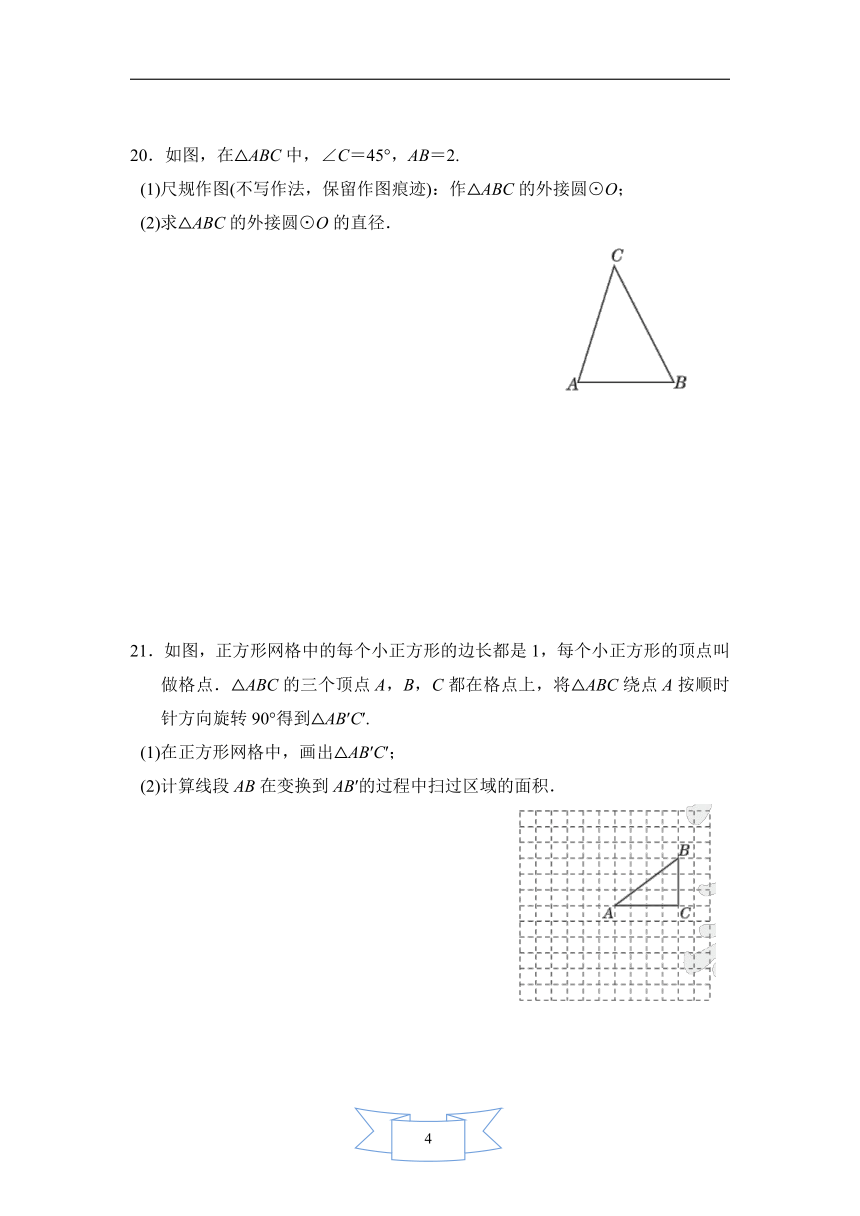
20.如图,在△ABC中,∠C=45°,AB=2.
(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)求△ABC的外接圆⊙O的直径.
21.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
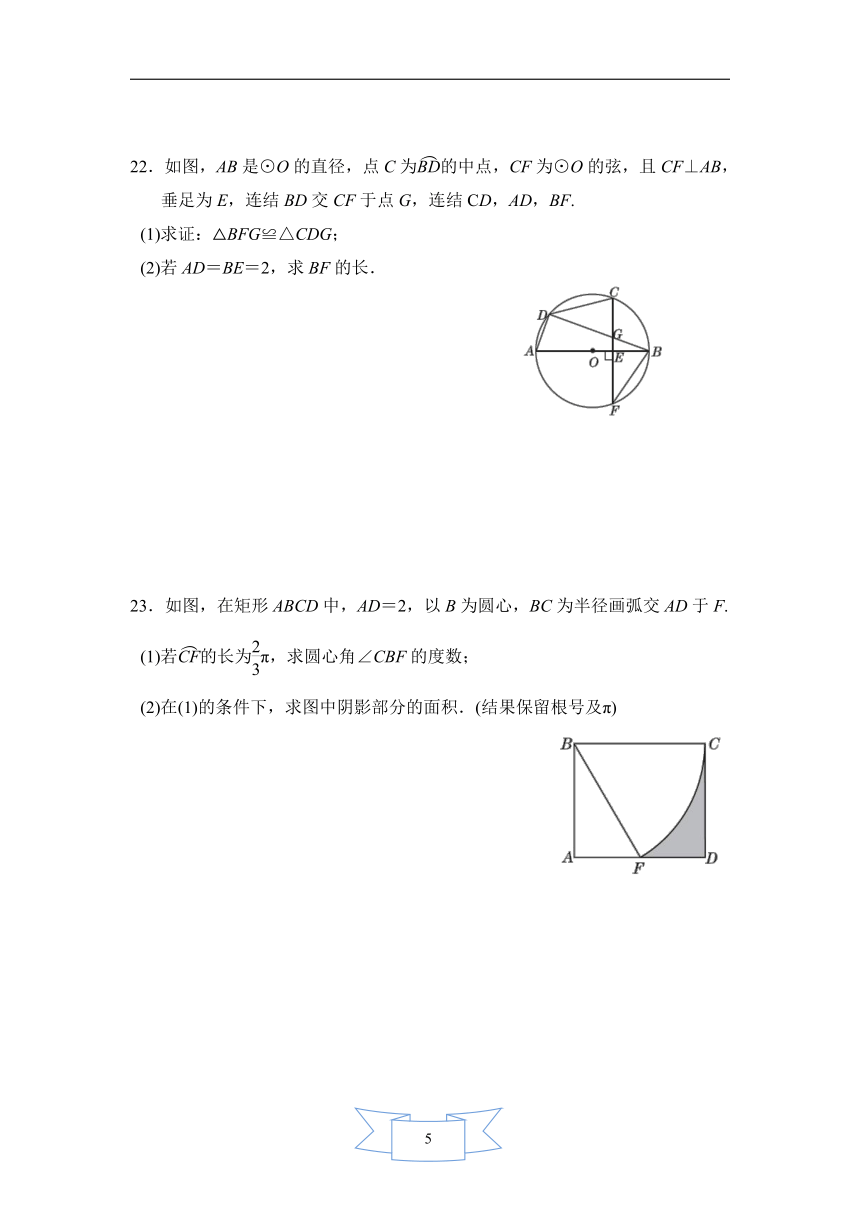
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连结BD交CF于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在矩形ABCD中,AD=2,以B为圆心,BC为半径画弧交AD于F.
(1)若的长为π,求圆心角∠CBF的度数;
(2)在(1)的条件下,求图中阴影部分的面积.(结果保留根号及π)
24.如图,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
答案
一、1.C 2.D 3.C 4.B 5.B 6.D 7.B
8.A 点拨:∵扇形AOB的圆心角为90°,半径为2
cm,∴扇形AOB的面积为=π(cm2),两个半圆形的面积均为×π×12=(cm2).
如图,连结OD,BD,DA,
易知A,B,D三点共线.易得BD=OD=DA=
cm,且两个半圆形内的4个小弓形面积相等.
在半圆形OA中,S弓形AD=(S半圆形OA-S△OAD)=cm2,∴S阴影=S扇形AOB-S△AOB-2S弓形AD=π-×2×2-2×=-1
(cm2).
9.C 点拨:当动点P在OC上运动时,∠APB逐渐变小;当动点P在上运动时,∠APB不变;当动点P在DO上运动时,∠APB逐渐变大.
10.A
二、11.50 12. 13.6 14.
15.3
cm
16.
点拨:在Rt△AOB中,由∠AOB=30°,易得OA=2AB=2.过点B作BD⊥OA于点D,在Rt△ABD中,易得AD=,BD=,∴OD=2-=,∴点B的坐标是.由三角尺AOB绕点O顺时针旋转90°得到△A′OB′,易得点B′的坐标是.
17.π-4
18.5或5 点拨:分情况讨论:如图①,当∠ODB=90°,即CD⊥AB时,
可得AD=BD,∴CD垂直平分AB,
∴AC=BC.
又∵AB=AC,∴△ABC是等边三角形.
易得∠DBO=30°.
由OB=5,
易得BD=OB=,
∴BC=AB=2BD=5
.
如图②,当∠DOB=90°时,
可得∠BOC=90°,又OB=OC,
∴△BOC是等腰直角三角形.
∴BC=OB=5
.
三、19.证明:连结BM.∵AP⊥BC,
∴∠CAP=90°-∠C.
∵AM为⊙O的直径,∴∠ABM=90°,
∴∠BAM=90°-∠M.
又∵∠M=∠C,
∴∠BAM=∠CAP.
20.解:(1)作图略.
(2)作直径AD,连结BD.
∵AD是直径,∴∠ABD=90°.
∵∠D=∠C=45°,∴AB=BD=2.
∴AD===2
,即△ABC的外接圆⊙O的直径为2
.
21.解:(1)△AB′C′如图所示.
(2)根据网格图,可知AB==5.
易知线段AB在变换到AB′的过程中,扫过区域为圆心角为90°,半径为5的扇形,其面积S=π·52=π.
22.(1)证明:∵C是的中点,∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,∴CD=BF.
在△BFG和△CDG中,
∵
∴△BFG≌△CDG(AAS).
(2)解:连结OF,设⊙O的半径为r,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴BD2=AB2-AD2,即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,∴=,
∴BD=CF,易得EF=CE,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2.
23.解:(1)设∠CBF=n°,
∵的长为π,半径R=BC=AD=2,
∴=π,∴n=60,
即∠CBF的度数为60°.
(2)∵∠CBF=60°,且四边形ABCD为矩形,∴∠ABF=30°.
在Rt△ABF中,易得AF=BF=AD=1,
∴AB===.
易得S扇形CBF==π,
S矩形ABCD=AD·AB=2×=2
,
S△ABF=AF·AB=×1×=,∴S阴影=S矩形ABCD-(S扇形CBF+S△ABF)=2-=-π.
24.(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,
易得O为EF的中点,即OE=OF.
又∵OA=OB,
∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8
cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
一、选择题(每题3分,共30分)
1.如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )
A.15°
B.60°
C.45°
D.75°
2.如图,已知AB和CD是⊙O的两条直径,连结AD,BC,则α和β的关系是( )
A.α=β
B.β>2α
C.β<2α
D.β=2α
3.如图,要拧开一个边长为6
mm的正六边形螺帽,扳手张开的开口a至少为( )
A.6
mm
B.12
mm
C.6
mm
D.4
mm
4.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B
5.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )
A.60°
B.50°
C.40°
D.20°
6.点A,B,C,D分别是⊙O上不同的四点,∠ABC=65°,则∠ADC=( )
A.65°
B.115°
C.25°
D.65°或115°
7.如图,某厂生产横截面直径为7
cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳的视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )
A.
cm
B.
cm
C.
cm
D.7π
cm
8.如图,在半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
A.cm2
B.cm2
C.1
cm2
D.cm2
9.如图,已知点A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿OC——DO的路线做匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y(度)与t(秒)之间的函数关系最恰当的是( )
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A.
B.1
C.2
D.2
二、填空题(每题3分,共24分)
11.如图,A,B,C是⊙O上的三点,∠AOB=100°,则∠ACB=________°.
12.同圆的内接正三角形与内接正方形的边长的比值是________.
13.如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E.若DE=3,则BC=________.
14.如图,△ABC是等边三角形,以BC为直径作圆O分别交AB,AC于点D,E,若BC=1,则DC=__________.
15.如图,已知⊙O的直径CD垂直于弦AB,垂足为E,∠AOD=45°,若CD=6
cm,则AB的长为________.
16.如图,将放置于平面直角坐标系中的三角尺AOB绕点O顺时针旋转90°得到△A′OB′.已知∠AOB=30°,∠B=90°,AB=1,则点B′的坐标是__________.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,分别以AC,BC为直径作半圆,则图中阴影部分的面积为________.
18.半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连结OB,OC,延长CO交弦AB于点D,若△OBD是直角三角形,则弦BC的长为____________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径.求证:∠BAM=∠CAP.
20.如图,在△ABC中,∠C=45°,AB=2.
(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)求△ABC的外接圆⊙O的直径.
21.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连结BD交CF于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在矩形ABCD中,AD=2,以B为圆心,BC为半径画弧交AD于F.
(1)若的长为π,求圆心角∠CBF的度数;
(2)在(1)的条件下,求图中阴影部分的面积.(结果保留根号及π)
24.如图,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
答案
一、1.C 2.D 3.C 4.B 5.B 6.D 7.B
8.A 点拨:∵扇形AOB的圆心角为90°,半径为2
cm,∴扇形AOB的面积为=π(cm2),两个半圆形的面积均为×π×12=(cm2).
如图,连结OD,BD,DA,
易知A,B,D三点共线.易得BD=OD=DA=
cm,且两个半圆形内的4个小弓形面积相等.
在半圆形OA中,S弓形AD=(S半圆形OA-S△OAD)=cm2,∴S阴影=S扇形AOB-S△AOB-2S弓形AD=π-×2×2-2×=-1
(cm2).
9.C 点拨:当动点P在OC上运动时,∠APB逐渐变小;当动点P在上运动时,∠APB不变;当动点P在DO上运动时,∠APB逐渐变大.
10.A
二、11.50 12. 13.6 14.
15.3
cm
16.
点拨:在Rt△AOB中,由∠AOB=30°,易得OA=2AB=2.过点B作BD⊥OA于点D,在Rt△ABD中,易得AD=,BD=,∴OD=2-=,∴点B的坐标是.由三角尺AOB绕点O顺时针旋转90°得到△A′OB′,易得点B′的坐标是.
17.π-4
18.5或5 点拨:分情况讨论:如图①,当∠ODB=90°,即CD⊥AB时,
可得AD=BD,∴CD垂直平分AB,
∴AC=BC.
又∵AB=AC,∴△ABC是等边三角形.
易得∠DBO=30°.
由OB=5,
易得BD=OB=,
∴BC=AB=2BD=5
.
如图②,当∠DOB=90°时,
可得∠BOC=90°,又OB=OC,
∴△BOC是等腰直角三角形.
∴BC=OB=5
.
三、19.证明:连结BM.∵AP⊥BC,
∴∠CAP=90°-∠C.
∵AM为⊙O的直径,∴∠ABM=90°,
∴∠BAM=90°-∠M.
又∵∠M=∠C,
∴∠BAM=∠CAP.
20.解:(1)作图略.
(2)作直径AD,连结BD.
∵AD是直径,∴∠ABD=90°.
∵∠D=∠C=45°,∴AB=BD=2.
∴AD===2
,即△ABC的外接圆⊙O的直径为2
.
21.解:(1)△AB′C′如图所示.
(2)根据网格图,可知AB==5.
易知线段AB在变换到AB′的过程中,扫过区域为圆心角为90°,半径为5的扇形,其面积S=π·52=π.
22.(1)证明:∵C是的中点,∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,∴CD=BF.
在△BFG和△CDG中,
∵
∴△BFG≌△CDG(AAS).
(2)解:连结OF,设⊙O的半径为r,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴BD2=AB2-AD2,即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,∴=,
∴BD=CF,易得EF=CE,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2.
23.解:(1)设∠CBF=n°,
∵的长为π,半径R=BC=AD=2,
∴=π,∴n=60,
即∠CBF的度数为60°.
(2)∵∠CBF=60°,且四边形ABCD为矩形,∴∠ABF=30°.
在Rt△ABF中,易得AF=BF=AD=1,
∴AB===.
易得S扇形CBF==π,
S矩形ABCD=AD·AB=2×=2
,
S△ABF=AF·AB=×1×=,∴S阴影=S矩形ABCD-(S扇形CBF+S△ABF)=2-=-π.
24.(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,
易得O为EF的中点,即OE=OF.
又∵OA=OB,
∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8
cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
同课章节目录
