6.3 反比例函数的应用(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 6.3 反比例函数的应用(知识清单+经典例题+夯实基础+提优特训+中考链接) |
|
|
| 格式 | zip | ||
| 文件大小 | 905.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 17:00:54 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.3
反比例函数的应用
【知识清单】
建立数学模型的过程,具体内容可概括为:
由实验获取数据——用描点法画出图象——根据图象和数据判断或估计函数的类别——用待定系数法求出函数关系式——用实验数据验证函数关系式——应用函数关系式解决问题
【经典例题】
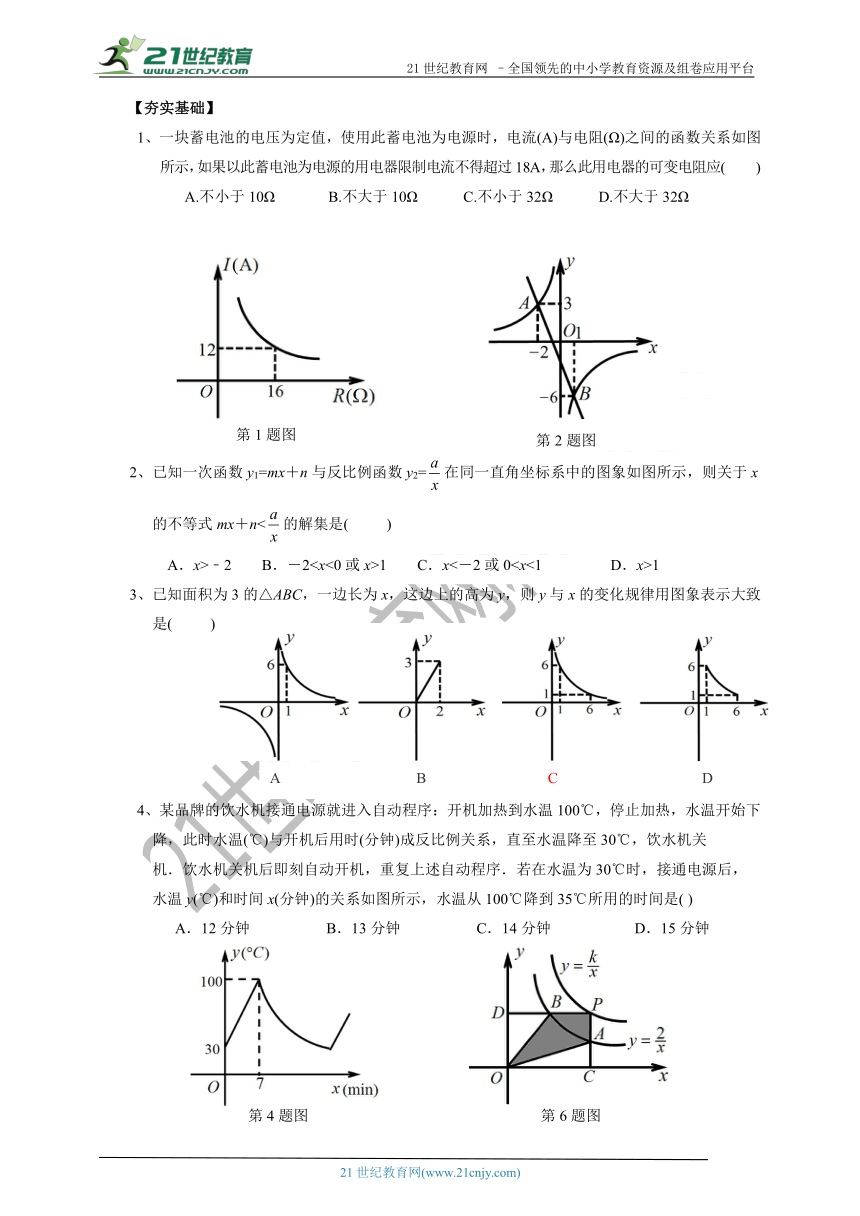
例题1、如果矩形的面积为21cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( )
【考点】反比例函数的实际应用.
【分析】根据题意有:xy=21;故y与x之间的函数图象为反比例函数,且根据x、y实际意义
x>0、y>0,其图象在第一象限,即可得出答案.
【解答】由矩形的面积公式可得xy=21,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
【点评】考查了反比例函数的应用和反比例函数的图象.现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
例题2、如图,在平面直角坐标系中,函数y=(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM:
MA=2:1,若AB=3,那么点N的坐标为
.
【考点】反比例函数的实际应用.
【分析】?根据等边三角形的性质和已知条件,可求出OM,
通过做垂线,利用解直角三角形,求出点M的坐标,进而
确定反比例函数的关系式;点N在双曲线上,而它的纵横
坐标都不知道,因此可以用直线AB的关系式与反比例函数
的关系式组成方程组,解出x、y的值,再进行取舍即可.
【解答】
答案在后面.
【点评】考查等边三角形的性质、待定系数法求函数的表达式、以及将两个函数的关系式组成方程组,通过解方程组求出交点坐标,在此仅求交点的横坐标即可,也就是求出方程组中的x的值.
【夯实基础】
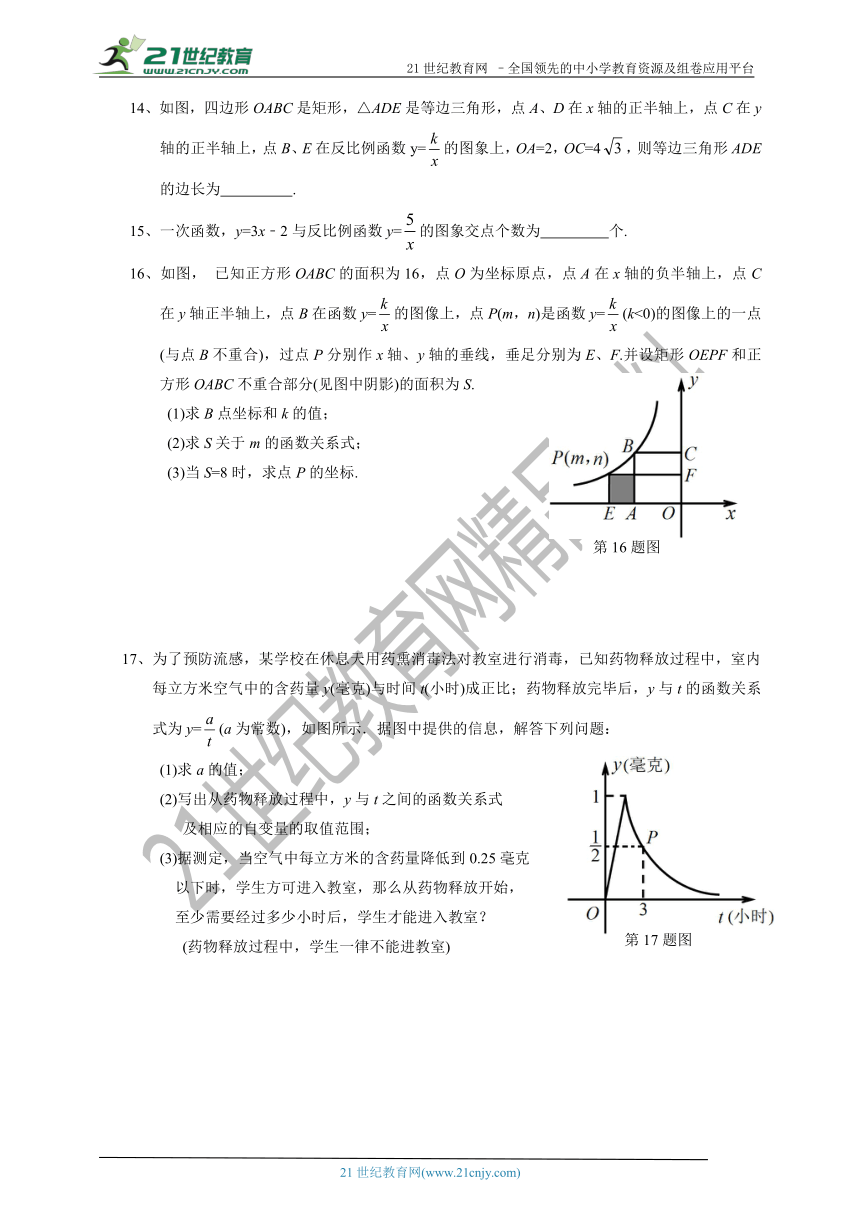
1、一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过18A,那么此用电器的可变电阻应(
)
A.不小于10Ω
B.不大于10Ω
C.不小于32Ω
D.不大于32Ω
2、已知一次函数y1=mx+n与反比例函数y2=在同一直角坐标系中的图象如图所示,则关于x的不等式mx+n<的解集是(
)
A.x>﹣2
B.-21
C.x<-2或0D.x>1
3、已知面积为3的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致
是(
)
4、某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下
降,此时水温(℃)与开机后用时(分钟)成反比例关系,直至水温降至30℃,饮水机关
机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,
水温y(℃)和时间x(分钟)的关系如图所示,水温从100℃降到35℃所用的时间是(?)
A.12分钟
B.13分钟
C.14分钟
D.15分钟
5、反比例函数y=,当x>0时,y
0,且y随x的增大而
.
6、两个反比例函数y=和y=在第一象限内的图象如图所示,点P在y=的图象上,PC⊥x轴于点C,交y=的图象于点A,PD⊥y轴于点D,交y=的图象于点B,当点P在y=的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是
(把你认为正确结论的序号都填上)
7、麦收到来之际,某储备库为收购小麦减少库存,需要将6000吨粮食转移到其他储备库中(方案定后,每天的运量不变).
(1)从运输开始,每天运输的粮食吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关
系式?
(2)因装卸工人短缺,实际每天比原计划少运25%,所以推迟2天完成任务,求原计划完成任
务的天数.
8、在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为8,你认为圆圆和方方
的说法对吗?为什么?
9、如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=(m<0)的图象交于
点B(﹣2,n),过点B作BC⊥x轴于点C,且BC平分∠ABP,点P(﹣n+3,2)是该反比例函数图象上的一点.
(1)求反比例函数和一次函数的表达式;
(2)求△POB的面积.
【提优特训】
10、如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=和y=的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积(图中阴影部分)为(
).
A.5?
B.7?
C.9?
D.14
11、如图.点A是反比例数y=图象上一点,过点A作x轴的垂线.垂足为
B点.若AB=10,
则四边形ABCD的周长为(???
)
A.?
B.?
C.?或
D.
或
12、两个反比例函数y=,y=在第一象限内的图象如图所示,点P1,P2,P3……P2020,在反比例函数y=的图象上,它们的横坐标分别是x1,x2,x3,…x2020,纵坐标分别是1,3,
5,…,共有2020个连续奇数,过点P1,P2,P3,…,P2020分别作y轴的平行线与y=的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2020(x2020,y2020),则y2020=(
)
A.4039
B.2019
.5?
C.2018.5
D.2017.5
13、如图,反比例函数y=与一次函数y=k2x﹣k2+在同一直角坐标系中的图象相交于A,B
两点,其中A(﹣2,3),直线k2x﹣k2+与坐标轴分别交于C,D两点,下列说法:
①k1<k2<0;②点B的坐标为(3,﹣2);③OD/OC=;④不等式>
k2x﹣k2+的解为
﹣2A.①③
?B.①②④??
??
C.①③⑤??
??
D.①③④⑤
14、如图,四边形OABC是矩形,△ADE是等边三角形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y=的图象上,OA=2,OC=4,则等边三角形ADE的边长为?????????
.
15、一次函数,y=3x﹣2与反比例函数y=的图象交点个数为
个.
16、如图,
已知正方形OABC的面积为16,点O为坐标原点,点A在x轴的负半轴上,点C在y轴正半轴上,点B在函数y=的图像上,点P(m,n)是函数y=(k<0)的图像上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设矩形OEPF和正方形OABC不重合部分(见图中阴影)的面积为S.
(1)求B点坐标和k的值;
(2)求S关于m的函数关系式;
(3)当S=8时,求点P的坐标.
17、为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=(a为常数),如图所示.据图中提供的信息,解答下列问题:
(1)求a的值;
(2)写出从药物释放过程中,y与t之间的函数关系式
及相应的自变量的取值范围;
(3)据测定,当空气中每立方米的含药量降低到0.25毫克
以下时,学生方可进入教室,那么从药物释放开始,
至少需要经过多少小时后,学生才能进入教室?
(药物释放过程中,学生一律不能进教室)
18、如图,反比例函数y=(k为常数,k≠0)的图象经过A(2,8),B(2m,2m).
(1)求反比例函数的解析式和m的值;
(2)在y轴上找一点P,使PA+PB的值最小,
求满足条件的点P的坐标;
(3)在x轴上找一点Q,使QA﹣QB的值最大,
求满足条件的点Q的坐标.
【中考链接】
19、(2019?孝感)
如图双曲线y=经过矩形OABC的顶点B,双曲线y=(x>0),交AB、BC于点E、F,且于矩形的对角线OB交于的D,
连接EF,若OD:OB=2:3,则△BEF的面积
为
.
20、(2019?济南)如图1,点A(0,8)、点B(2,a)在直线y=﹣2x+b上,反比例函数y=
(x>0)的图象经过点B.
(1)求a和k的值;
(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC、BD.
①如图2,当m=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;
②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三形,求所有满足条件的m的值.
参考答案
1、A
2、B
3、C
4、B
5、<、增大
6、①②④
10、B
11、C
12、B
13、C
14、4
15、2
19、
例题2答案:过点A、M分别作AC⊥OB,MD⊥OB,垂足为C、D,
∵△AOB是等边三角形,
∴AB=OA=OB=3,∠AOB=60°
∵又OM:
MA=2:1,
∴OM=2,MA=1,
在Rt△MOD中,
OD=OM=1,MD==,
∴M(1,);
∴反比例函数的关系式为:y=
在Rt△AOC中,
OC=OA=,AC==,
∴A(,),
设直线AB的关系式为y=kx+b,把A(,),B(3,0)代入得:
?
?解得:k=﹣,b=,
∴y=﹣x+;
由题意得:??解得:,,
∵x、y都在第一象限,且x>,∴,
故点N的坐标为:
7、解:(1)∵每天运量×天数=总运量,∴nt=4000.
∴.
(2)设原计划x天完成,
根据题意得:,
解得:x=6.
经检验:x=6是原方程的根.
答:原计划6天完成.
8、解:(1)①由题意可得:xy=3,
则y=;
②当y≥3时,≥3,解得:x≤1;
(2)∵一个矩形的周长为6,
∴x+y=3,
∴x+=3,
整理得:x2﹣3x+3=0,
∵b2﹣4ac=9﹣12=﹣3<0,
∴矩形的周长不可能是6;
∵一个矩形的周长为8,
∴x+y=4,
∴x+=4,
整理得:x2﹣4x+3=0,
∵b2﹣4ac=16﹣12=4>0,
∴矩形的周长可能是8.
9、解:(1)∵点B(﹣2,n)、P(﹣n+3,2)
在反比例函数y=(m<0)的图象上,
∴,解得:m=﹣12,n=6.
∴反比例函数的表达式为y=.
∵
m=﹣12,n=6,
∴点B(﹣2,6),P(﹣6,2).
过点P作PD⊥BC,垂足为D,并延长交AB与点P′.
∵BC平分∠ABP,
∴∠PBC=∠ABC.
在△BDP和△BDP′中,
∵
∴△BDP≌△BDP′.
∴DP′=DP=4.
∴点P′(2,2).
将点P′(2,2),B(﹣2,6)代入直线的解析式y=kx+b得:,
解得:.
∴一次函数的表达式为y=x+4.
(2)
过点P作PE⊥x轴,垂足为E,
则PE=2,OE=6,BC=6,CO=2,
S△POB=
S△COB+
S梯形PECB﹣
S△PEO
=CO·BC+(PE+BC)·EC﹣PE·EO
=×2×6+×(2+6)×(6﹣2)﹣×2×6
=16.
16、解:(1)∵正方形OABC的面积为4,
??????????????
?∴OA=OC=4,
???????????????
∴B点坐标为(﹣4,4),
???????????????
∵点B(﹣4,4)在函数y=的图像上,
???????????????
∴4=,即k=﹣16.
(2)当m<﹣4时,S=AE·PE=(﹣m﹣4)·=16+,
????
当﹣4(3)当S=8时,
??
??
16+=8或16+4m
=8,
???
解得:m=﹣8或m=﹣2,
??
?
所以n=2或n=8,
???
所以P点坐标为(﹣8,2)或(﹣2,8).
17、
解:(1)将点P(3,)
代入y=中,
解得a=
(2)所以所求反比例函数关系式为y=(t≥),
将y=1代入y=,得
t=,
再将(,1)代入y=kt,得k=,
所以正比例函数关系式为y=t(0≤t≤).
(3)解不等式<,解得t>6,
所以至少需要经过6小时后,学生才能进入教室.
18、解:(1)如图①,
∵反比例函数y=(k为常数,k≠0)的图象经过A(2,8),
∴k=xy=2×8=16,
∴反比例函数的解析式为y=,
∵A(2,8),B(2m,2m)在同一条反比例函数y=图象上,
∴2×8=2m×2m
解得m=±2,
∵点B在第一象限,
∴m>0,
∴m=2,
∴B点的坐标为(4,4);
(2)
如图②,作出A关于y轴的对称点,
则的坐标为(﹣2,8),
连接B交y轴于点P,
设直线B的解析式为y=kx+b,
将(﹣2,8),B(4,4)代入得,
解得,
∴直线B的解析式为y=
x+,
令x=0,则y=,∴点P的坐标为(0,);
(3)
如图③,要使QA﹣QB的值最大,则A、B、P必须在一条直线上,
设直线AB的解析式为y=mx+n,
将A(2,8),B(4,4)代入得,
解得,
∴直线B的解析式为y=
x+,
令y=0,则x=6,∴点Q的坐标为(6,0);
20.解:(1)∵点A(0,8)在直线y=﹣2x+b上,
∴﹣2×0+b=8,
∴b=8,
∴直线AB的解析式为y=﹣2x+8,
将点B(2,a)代入直线AB的解析式y=﹣2x+8中,得﹣2×2+8=a,
∴a=4,
∴B(2,4),
将B(2,4)在反比例函数解析式y=(x>0)中,得k=xy=2×4=8;
(2)①由(1)知,B(2,4),k=8,∴反比例函数解析式为y=,
当m=3时,
∴将线段AB向右平移3个单位长度,得到对应线段CD,
∴D(2+3,4),
即:D(5,4),
∵DF⊥x轴于点F,交反比例函数y=的图象于点E,
∴E(5,),
∴DE=4﹣=,EF=,
∴==;
②如图,∵将线段AB向右平移m个单位长度(m>0),得到对应线段CD,
∴CD=AB,AC=BD=m,
∵A(0,8),B(2,4),
∴C(m,8),D((m+2,4),
∵△BCD是以BC为腰的等腰三形,
∴Ⅰ、当BC=CD时,
∴BC=AB,
∴点B在线段AC的垂直平分线上,
∴m=2×2=4,
Ⅱ、当BC=BD时,
∵B(2,4),C(m,8),
∴BC=,
∴=m,
∴m=5,
即:△BCD是以BC为腰的等腰三形,满足条件的m的值为4或5.
第9题图
第10题图
第12题图
第13题图
第16题图
第9题图
例题2图
第17题图
第18题图①
第9题图
第17题图
第2题图
第18题图①
第6题图
第19题图
例题2图
第1题图
第17题图
第16题图
A
B
C
D
第20题图1
第20题图2
第4题图
第14题图
第11题图
第10题图
A
B
C
D
第18题图
第18题图②
第18题图③
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第6章反比例函数
6.3
反比例函数的应用
【知识清单】
建立数学模型的过程,具体内容可概括为:
由实验获取数据——用描点法画出图象——根据图象和数据判断或估计函数的类别——用待定系数法求出函数关系式——用实验数据验证函数关系式——应用函数关系式解决问题
【经典例题】
例题1、如果矩形的面积为21cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( )
【考点】反比例函数的实际应用.
【分析】根据题意有:xy=21;故y与x之间的函数图象为反比例函数,且根据x、y实际意义
x>0、y>0,其图象在第一象限,即可得出答案.
【解答】由矩形的面积公式可得xy=21,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
【点评】考查了反比例函数的应用和反比例函数的图象.现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
例题2、如图,在平面直角坐标系中,函数y=(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM:
MA=2:1,若AB=3,那么点N的坐标为
.
【考点】反比例函数的实际应用.
【分析】?根据等边三角形的性质和已知条件,可求出OM,
通过做垂线,利用解直角三角形,求出点M的坐标,进而
确定反比例函数的关系式;点N在双曲线上,而它的纵横
坐标都不知道,因此可以用直线AB的关系式与反比例函数
的关系式组成方程组,解出x、y的值,再进行取舍即可.
【解答】
答案在后面.
【点评】考查等边三角形的性质、待定系数法求函数的表达式、以及将两个函数的关系式组成方程组,通过解方程组求出交点坐标,在此仅求交点的横坐标即可,也就是求出方程组中的x的值.
【夯实基础】
1、一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过18A,那么此用电器的可变电阻应(
)
A.不小于10Ω
B.不大于10Ω
C.不小于32Ω
D.不大于32Ω
2、已知一次函数y1=mx+n与反比例函数y2=在同一直角坐标系中的图象如图所示,则关于x的不等式mx+n<的解集是(
)
A.x>﹣2
B.-2
C.x<-2或0
3、已知面积为3的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致
是(
)
4、某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下
降,此时水温(℃)与开机后用时(分钟)成反比例关系,直至水温降至30℃,饮水机关
机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,
水温y(℃)和时间x(分钟)的关系如图所示,水温从100℃降到35℃所用的时间是(?)
A.12分钟
B.13分钟
C.14分钟
D.15分钟
5、反比例函数y=,当x>0时,y
0,且y随x的增大而
.
6、两个反比例函数y=和y=在第一象限内的图象如图所示,点P在y=的图象上,PC⊥x轴于点C,交y=的图象于点A,PD⊥y轴于点D,交y=的图象于点B,当点P在y=的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是
(把你认为正确结论的序号都填上)
7、麦收到来之际,某储备库为收购小麦减少库存,需要将6000吨粮食转移到其他储备库中(方案定后,每天的运量不变).
(1)从运输开始,每天运输的粮食吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关
系式?
(2)因装卸工人短缺,实际每天比原计划少运25%,所以推迟2天完成任务,求原计划完成任
务的天数.
8、在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为8,你认为圆圆和方方
的说法对吗?为什么?
9、如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=(m<0)的图象交于
点B(﹣2,n),过点B作BC⊥x轴于点C,且BC平分∠ABP,点P(﹣n+3,2)是该反比例函数图象上的一点.
(1)求反比例函数和一次函数的表达式;
(2)求△POB的面积.
【提优特训】
10、如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=和y=的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积(图中阴影部分)为(
).
A.5?
B.7?
C.9?
D.14
11、如图.点A是反比例数y=图象上一点,过点A作x轴的垂线.垂足为
B点.若AB=10,
则四边形ABCD的周长为(???
)
A.?
B.?
C.?或
D.
或
12、两个反比例函数y=,y=在第一象限内的图象如图所示,点P1,P2,P3……P2020,在反比例函数y=的图象上,它们的横坐标分别是x1,x2,x3,…x2020,纵坐标分别是1,3,
5,…,共有2020个连续奇数,过点P1,P2,P3,…,P2020分别作y轴的平行线与y=的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2020(x2020,y2020),则y2020=(
)
A.4039
B.2019
.5?
C.2018.5
D.2017.5
13、如图,反比例函数y=与一次函数y=k2x﹣k2+在同一直角坐标系中的图象相交于A,B
两点,其中A(﹣2,3),直线k2x﹣k2+与坐标轴分别交于C,D两点,下列说法:
①k1<k2<0;②点B的坐标为(3,﹣2);③OD/OC=;④不等式>
k2x﹣k2+的解为
﹣2
?B.①②④??
??
C.①③⑤??
??
D.①③④⑤
14、如图,四边形OABC是矩形,△ADE是等边三角形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y=的图象上,OA=2,OC=4,则等边三角形ADE的边长为?????????
.
15、一次函数,y=3x﹣2与反比例函数y=的图象交点个数为
个.
16、如图,
已知正方形OABC的面积为16,点O为坐标原点,点A在x轴的负半轴上,点C在y轴正半轴上,点B在函数y=的图像上,点P(m,n)是函数y=(k<0)的图像上的一点(与点B不重合),过点P分别作x轴、y轴的垂线,垂足分别为E、F.并设矩形OEPF和正方形OABC不重合部分(见图中阴影)的面积为S.
(1)求B点坐标和k的值;
(2)求S关于m的函数关系式;
(3)当S=8时,求点P的坐标.
17、为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=(a为常数),如图所示.据图中提供的信息,解答下列问题:
(1)求a的值;
(2)写出从药物释放过程中,y与t之间的函数关系式
及相应的自变量的取值范围;
(3)据测定,当空气中每立方米的含药量降低到0.25毫克
以下时,学生方可进入教室,那么从药物释放开始,
至少需要经过多少小时后,学生才能进入教室?
(药物释放过程中,学生一律不能进教室)
18、如图,反比例函数y=(k为常数,k≠0)的图象经过A(2,8),B(2m,2m).
(1)求反比例函数的解析式和m的值;
(2)在y轴上找一点P,使PA+PB的值最小,
求满足条件的点P的坐标;
(3)在x轴上找一点Q,使QA﹣QB的值最大,
求满足条件的点Q的坐标.
【中考链接】
19、(2019?孝感)
如图双曲线y=经过矩形OABC的顶点B,双曲线y=(x>0),交AB、BC于点E、F,且于矩形的对角线OB交于的D,
连接EF,若OD:OB=2:3,则△BEF的面积
为
.
20、(2019?济南)如图1,点A(0,8)、点B(2,a)在直线y=﹣2x+b上,反比例函数y=
(x>0)的图象经过点B.
(1)求a和k的值;
(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC、BD.
①如图2,当m=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;
②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三形,求所有满足条件的m的值.
参考答案
1、A
2、B
3、C
4、B
5、<、增大
6、①②④
10、B
11、C
12、B
13、C
14、4
15、2
19、
例题2答案:过点A、M分别作AC⊥OB,MD⊥OB,垂足为C、D,
∵△AOB是等边三角形,
∴AB=OA=OB=3,∠AOB=60°
∵又OM:
MA=2:1,
∴OM=2,MA=1,
在Rt△MOD中,
OD=OM=1,MD==,
∴M(1,);
∴反比例函数的关系式为:y=
在Rt△AOC中,
OC=OA=,AC==,
∴A(,),
设直线AB的关系式为y=kx+b,把A(,),B(3,0)代入得:
?
?解得:k=﹣,b=,
∴y=﹣x+;
由题意得:??解得:,,
∵x、y都在第一象限,且x>,∴,
故点N的坐标为:
7、解:(1)∵每天运量×天数=总运量,∴nt=4000.
∴.
(2)设原计划x天完成,
根据题意得:,
解得:x=6.
经检验:x=6是原方程的根.
答:原计划6天完成.
8、解:(1)①由题意可得:xy=3,
则y=;
②当y≥3时,≥3,解得:x≤1;
(2)∵一个矩形的周长为6,
∴x+y=3,
∴x+=3,
整理得:x2﹣3x+3=0,
∵b2﹣4ac=9﹣12=﹣3<0,
∴矩形的周长不可能是6;
∵一个矩形的周长为8,
∴x+y=4,
∴x+=4,
整理得:x2﹣4x+3=0,
∵b2﹣4ac=16﹣12=4>0,
∴矩形的周长可能是8.
9、解:(1)∵点B(﹣2,n)、P(﹣n+3,2)
在反比例函数y=(m<0)的图象上,
∴,解得:m=﹣12,n=6.
∴反比例函数的表达式为y=.
∵
m=﹣12,n=6,
∴点B(﹣2,6),P(﹣6,2).
过点P作PD⊥BC,垂足为D,并延长交AB与点P′.
∵BC平分∠ABP,
∴∠PBC=∠ABC.
在△BDP和△BDP′中,
∵
∴△BDP≌△BDP′.
∴DP′=DP=4.
∴点P′(2,2).
将点P′(2,2),B(﹣2,6)代入直线的解析式y=kx+b得:,
解得:.
∴一次函数的表达式为y=x+4.
(2)
过点P作PE⊥x轴,垂足为E,
则PE=2,OE=6,BC=6,CO=2,
S△POB=
S△COB+
S梯形PECB﹣
S△PEO
=CO·BC+(PE+BC)·EC﹣PE·EO
=×2×6+×(2+6)×(6﹣2)﹣×2×6
=16.
16、解:(1)∵正方形OABC的面积为4,
??????????????
?∴OA=OC=4,
???????????????
∴B点坐标为(﹣4,4),
???????????????
∵点B(﹣4,4)在函数y=的图像上,
???????????????
∴4=,即k=﹣16.
(2)当m<﹣4时,S=AE·PE=(﹣m﹣4)·=16+,
????
当﹣4
??
??
16+=8或16+4m
=8,
???
解得:m=﹣8或m=﹣2,
??
?
所以n=2或n=8,
???
所以P点坐标为(﹣8,2)或(﹣2,8).
17、
解:(1)将点P(3,)
代入y=中,
解得a=
(2)所以所求反比例函数关系式为y=(t≥),
将y=1代入y=,得
t=,
再将(,1)代入y=kt,得k=,
所以正比例函数关系式为y=t(0≤t≤).
(3)解不等式<,解得t>6,
所以至少需要经过6小时后,学生才能进入教室.
18、解:(1)如图①,
∵反比例函数y=(k为常数,k≠0)的图象经过A(2,8),
∴k=xy=2×8=16,
∴反比例函数的解析式为y=,
∵A(2,8),B(2m,2m)在同一条反比例函数y=图象上,
∴2×8=2m×2m
解得m=±2,
∵点B在第一象限,
∴m>0,
∴m=2,
∴B点的坐标为(4,4);
(2)
如图②,作出A关于y轴的对称点,
则的坐标为(﹣2,8),
连接B交y轴于点P,
设直线B的解析式为y=kx+b,
将(﹣2,8),B(4,4)代入得,
解得,
∴直线B的解析式为y=
x+,
令x=0,则y=,∴点P的坐标为(0,);
(3)
如图③,要使QA﹣QB的值最大,则A、B、P必须在一条直线上,
设直线AB的解析式为y=mx+n,
将A(2,8),B(4,4)代入得,
解得,
∴直线B的解析式为y=
x+,
令y=0,则x=6,∴点Q的坐标为(6,0);
20.解:(1)∵点A(0,8)在直线y=﹣2x+b上,
∴﹣2×0+b=8,
∴b=8,
∴直线AB的解析式为y=﹣2x+8,
将点B(2,a)代入直线AB的解析式y=﹣2x+8中,得﹣2×2+8=a,
∴a=4,
∴B(2,4),
将B(2,4)在反比例函数解析式y=(x>0)中,得k=xy=2×4=8;
(2)①由(1)知,B(2,4),k=8,∴反比例函数解析式为y=,
当m=3时,
∴将线段AB向右平移3个单位长度,得到对应线段CD,
∴D(2+3,4),
即:D(5,4),
∵DF⊥x轴于点F,交反比例函数y=的图象于点E,
∴E(5,),
∴DE=4﹣=,EF=,
∴==;
②如图,∵将线段AB向右平移m个单位长度(m>0),得到对应线段CD,
∴CD=AB,AC=BD=m,
∵A(0,8),B(2,4),
∴C(m,8),D((m+2,4),
∵△BCD是以BC为腰的等腰三形,
∴Ⅰ、当BC=CD时,
∴BC=AB,
∴点B在线段AC的垂直平分线上,
∴m=2×2=4,
Ⅱ、当BC=BD时,
∵B(2,4),C(m,8),
∴BC=,
∴=m,
∴m=5,
即:△BCD是以BC为腰的等腰三形,满足条件的m的值为4或5.
第9题图
第10题图
第12题图
第13题图
第16题图
第9题图
例题2图
第17题图
第18题图①
第9题图
第17题图
第2题图
第18题图①
第6题图
第19题图
例题2图
第1题图
第17题图
第16题图
A
B
C
D
第20题图1
第20题图2
第4题图
第14题图
第11题图
第10题图
A
B
C
D
第18题图
第18题图②
第18题图③
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
