四年级下册数学课件 整理与提高 小数与近似数 沪教版 (共21张PPT)
文档属性
| 名称 | 四年级下册数学课件 整理与提高 小数与近似数 沪教版 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 431.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 14:15:43 | ||
图片预览






文档简介
(共21张PPT)
小数与近似数(1)
教学目标:
1、能根据要求正确地运用“四舍五入法”求一个小数的近似数;
2、理解求一个小数的近似值,在表示一定的精确度时,小数末尾的“0”不能去掉;
3、理解表示小数的近似数,小数位数越多结果越精确。
4、感知四舍五入求近似数的方法在生活实际中的应用,并培养学生借助新、旧知识的内在联系,发展类比及推理的能力。
新课导入
(1)你知道上海市2016年年末的机动车数量吗?
至2016年年末上海市机动车约是334万辆
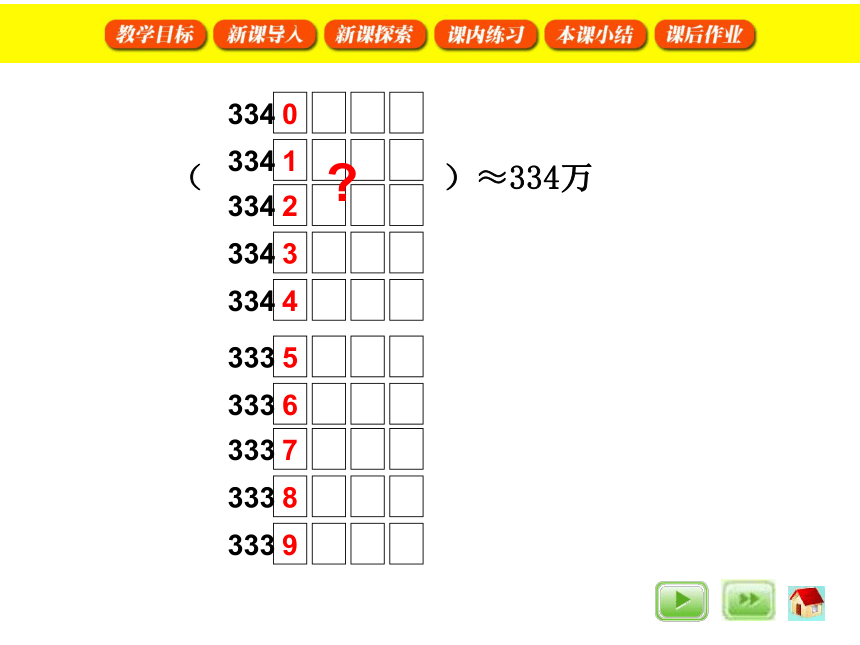
在取近似数的时候,如果尾数的最高位数字是4或者比4小,就把尾数去掉。如果尾数的最高位数是5或者比5大,就把尾数舍去并且在它的前一位进1,这种取近似数的方法叫做四舍五入法。
近似数
(
)≈334万
334
1
334
2
334
3
334
0
334
4
333
6
333
7
333
8
333
5
333
9
?
新课探索
探究一
探究二
探究三
探究一
探究一
探究二
探究三
0.984米
探究一
求整数的近似数可以用四舍五入法,求小数的近似数同样也可以用四舍五入法。
探究一
探究二
探究三
探究一
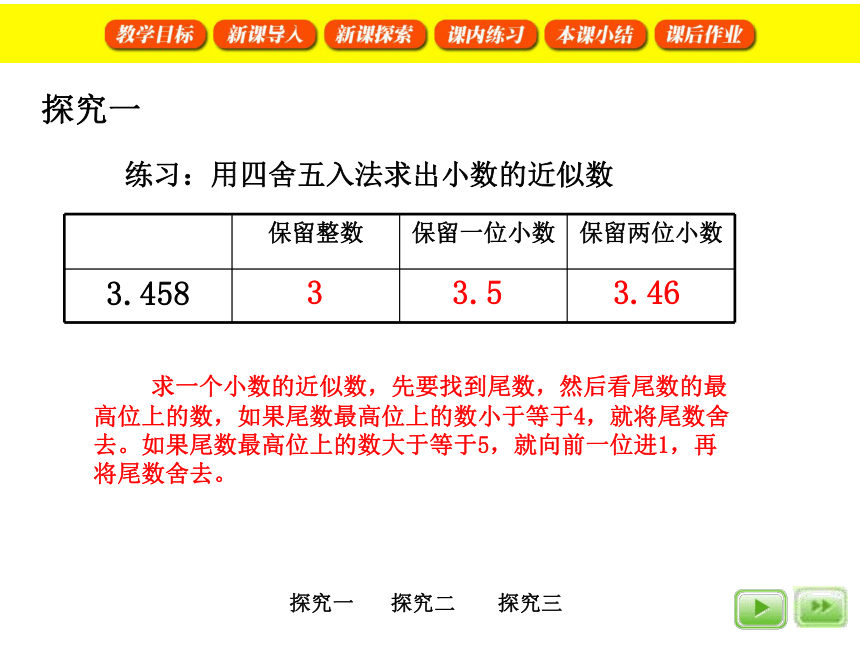
求一个小数的近似数,先要找到尾数,然后看尾数的最高位上的数,如果尾数最高位上的数小于等于4,就将尾数舍去。如果尾数最高位上的数大于等于5,就向前一位进1,再将尾数舍去。
探究一
探究二
探究三
练习:用四舍五入法求出小数的近似数
保留整数
保留一位小数
保留两位小数
3.458
3
3.5
3.46
练习:用四舍五入法求小数的近似数。
保留整数
保留一位小数
保留两位小数
12.006
12
12.0
12.01
探究一
探究二
探究三
探究二
用四舍五入法将12.006保留一位小数
12.006≈12.0
还是
12.006≈12
12.0是一位小数,12是整数;
12.0表示120个0.1,12表示12个1
探究一
探究二
探究三
探究二
怎样的数用四舍五入法保留一位小数约是12.0?
大于等于11.95,小于12.05的数
怎样的数用四舍五入法保留整数约是12?
大于等于11.
5,小于12.5的数
0.984米保留一位小数的结果?
0.984米≈1.0米
探究一
探究二
探究三
表示近似数时,小数末尾的0不能去掉。
练习:按要求用四舍五入法写出表中小数的近似数。
精确到个位
精确到十分位
精确到百分位
9.956
0.905
1.463
10
10.0
9.96
1
0.9
0.91
1
1.5
1.46
探究一
探究二
探究三
鲍老师的身高:1.71米
姚明身高:
2.26米
学生身高:1.52米
把它们分别保留整数、保留一位小数。
探究三
保留整数:
1.71米≈2米
2.26米≈2米
1.52米≈2米
保留一位小数:
1.71米≈1.7米
2.26米≈2.3米
1.52米≈1.5米
表示小数的近似数,小数位数越多结果越精确。
探究一
探究二
探究三
探究三
中国银行某年4月的汇率:
探究一
探究二
探究三
人民币
1美元
6.5294元
1港元
0.83957元
1欧元
9.3792元
探究三
用四舍五入法求近似数:
探究一
探究二
探究三
实际汇率
人民币(保留整数)
人民币(保留一位小数)
人民币(保留两位小数)
1美元
6.5294
元
1港元
0.83957
元
1欧元
9.3972
元
7元
6.5元
6.53元
1元
0.8元
0.84元
9元
9.4元
9.40元
课内练习
练习
1、老师初来郑州,昨天到超市去购买了一些物品,收银条上打的价钱一共是56.43元,你们认为老师应该付(
)元。
56.4
2、老师的身高大约是1.7米,老师实际身高是两位小数,猜一猜,老师的实际身高可能是(
)米?
1.71;1.72;1.73;1.74
1.65;1.66;1.67;1.68;1.69
本课小结
本课小结
1、在用四舍五入法求一个小数的近似数的时候,如果尾数的最高位数字是4或者比4小,就把尾数去掉。如果尾数的最高位数是5或者比5大,就把尾数舍去并且在它的前一位进1。
2、在表示近似数时,小数末尾的0不能去掉。
3、表示小数的近似数,小数位数越多结果越精确。
谢谢!
小数与近似数(1)
教学目标:
1、能根据要求正确地运用“四舍五入法”求一个小数的近似数;
2、理解求一个小数的近似值,在表示一定的精确度时,小数末尾的“0”不能去掉;
3、理解表示小数的近似数,小数位数越多结果越精确。
4、感知四舍五入求近似数的方法在生活实际中的应用,并培养学生借助新、旧知识的内在联系,发展类比及推理的能力。
新课导入
(1)你知道上海市2016年年末的机动车数量吗?
至2016年年末上海市机动车约是334万辆
在取近似数的时候,如果尾数的最高位数字是4或者比4小,就把尾数去掉。如果尾数的最高位数是5或者比5大,就把尾数舍去并且在它的前一位进1,这种取近似数的方法叫做四舍五入法。
近似数
(
)≈334万
334
1
334
2
334
3
334
0
334
4
333
6
333
7
333
8
333
5
333
9
?
新课探索
探究一
探究二
探究三
探究一
探究一
探究二
探究三
0.984米
探究一
求整数的近似数可以用四舍五入法,求小数的近似数同样也可以用四舍五入法。
探究一
探究二
探究三
探究一
求一个小数的近似数,先要找到尾数,然后看尾数的最高位上的数,如果尾数最高位上的数小于等于4,就将尾数舍去。如果尾数最高位上的数大于等于5,就向前一位进1,再将尾数舍去。
探究一
探究二
探究三
练习:用四舍五入法求出小数的近似数
保留整数
保留一位小数
保留两位小数
3.458
3
3.5
3.46
练习:用四舍五入法求小数的近似数。
保留整数
保留一位小数
保留两位小数
12.006
12
12.0
12.01
探究一
探究二
探究三
探究二
用四舍五入法将12.006保留一位小数
12.006≈12.0
还是
12.006≈12
12.0是一位小数,12是整数;
12.0表示120个0.1,12表示12个1
探究一
探究二
探究三
探究二
怎样的数用四舍五入法保留一位小数约是12.0?
大于等于11.95,小于12.05的数
怎样的数用四舍五入法保留整数约是12?
大于等于11.
5,小于12.5的数
0.984米保留一位小数的结果?
0.984米≈1.0米
探究一
探究二
探究三
表示近似数时,小数末尾的0不能去掉。
练习:按要求用四舍五入法写出表中小数的近似数。
精确到个位
精确到十分位
精确到百分位
9.956
0.905
1.463
10
10.0
9.96
1
0.9
0.91
1
1.5
1.46
探究一
探究二
探究三
鲍老师的身高:1.71米
姚明身高:
2.26米
学生身高:1.52米
把它们分别保留整数、保留一位小数。
探究三
保留整数:
1.71米≈2米
2.26米≈2米
1.52米≈2米
保留一位小数:
1.71米≈1.7米
2.26米≈2.3米
1.52米≈1.5米
表示小数的近似数,小数位数越多结果越精确。
探究一
探究二
探究三
探究三
中国银行某年4月的汇率:
探究一
探究二
探究三
人民币
1美元
6.5294元
1港元
0.83957元
1欧元
9.3792元
探究三
用四舍五入法求近似数:
探究一
探究二
探究三
实际汇率
人民币(保留整数)
人民币(保留一位小数)
人民币(保留两位小数)
1美元
6.5294
元
1港元
0.83957
元
1欧元
9.3972
元
7元
6.5元
6.53元
1元
0.8元
0.84元
9元
9.4元
9.40元
课内练习
练习
1、老师初来郑州,昨天到超市去购买了一些物品,收银条上打的价钱一共是56.43元,你们认为老师应该付(
)元。
56.4
2、老师的身高大约是1.7米,老师实际身高是两位小数,猜一猜,老师的实际身高可能是(
)米?
1.71;1.72;1.73;1.74
1.65;1.66;1.67;1.68;1.69
本课小结
本课小结
1、在用四舍五入法求一个小数的近似数的时候,如果尾数的最高位数字是4或者比4小,就把尾数去掉。如果尾数的最高位数是5或者比5大,就把尾数舍去并且在它的前一位进1。
2、在表示近似数时,小数末尾的0不能去掉。
3、表示小数的近似数,小数位数越多结果越精确。
谢谢!
