5.5平行四边形的判定（2）

(共21张PPT)
5.5 平行四边形的判定（2）
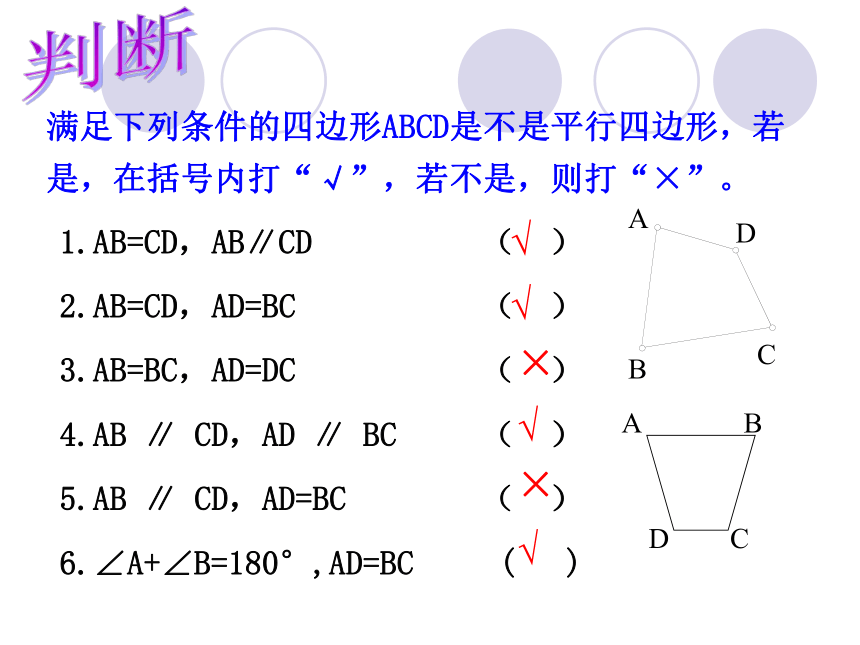
满足下列条件的四边形ABCD是不是平行四边形，若是，在括号内打“√”，若不是，则打“×”。
√
√
√
×
×
√
A
B
C
D
1.AB=CD，AB∥CD （ ）
2.AB=CD，AD=BC （ ）
3.AB=BC，AD=DC （ ）
4.AB ∥ CD，AD ∥ BC （ ）
5.AB ∥ CD，AD=BC （ ）
6.∠A+∠B=180°,AD=BC ( )
A
B
C
D
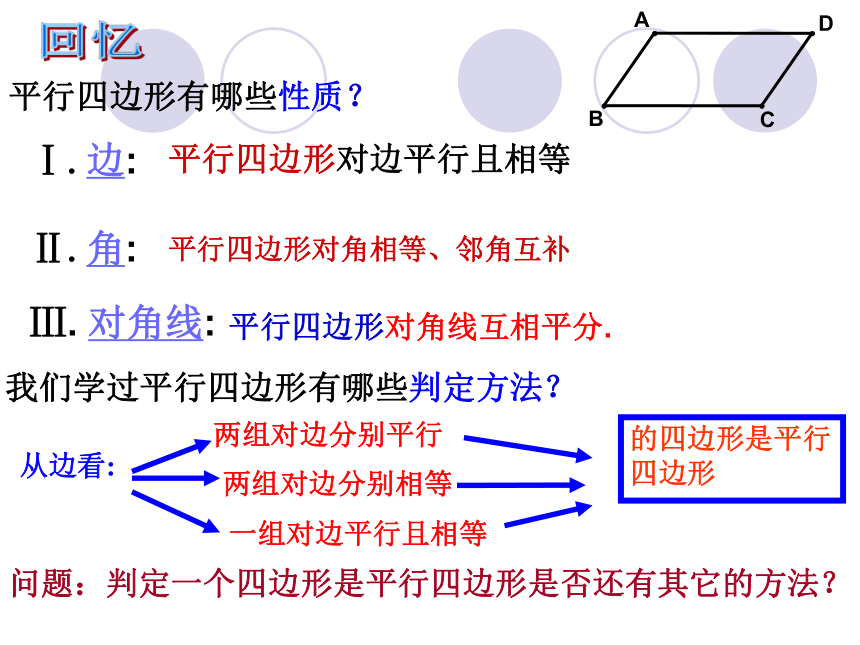
平行四边形有哪些性质？
Ⅰ.边:
Ⅱ.角:
Ⅲ. 对角线:
平行四边形对角线互相平分.
D
A
C
B
我们学过平行四边形有哪些判定方法？
从边看:
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形
问题：判定一个四边形是平行四边形是否还有其它的方法？
平行四边形对边平行且相等
平行四边形对角相等、邻角互补
A
C
O
B
D
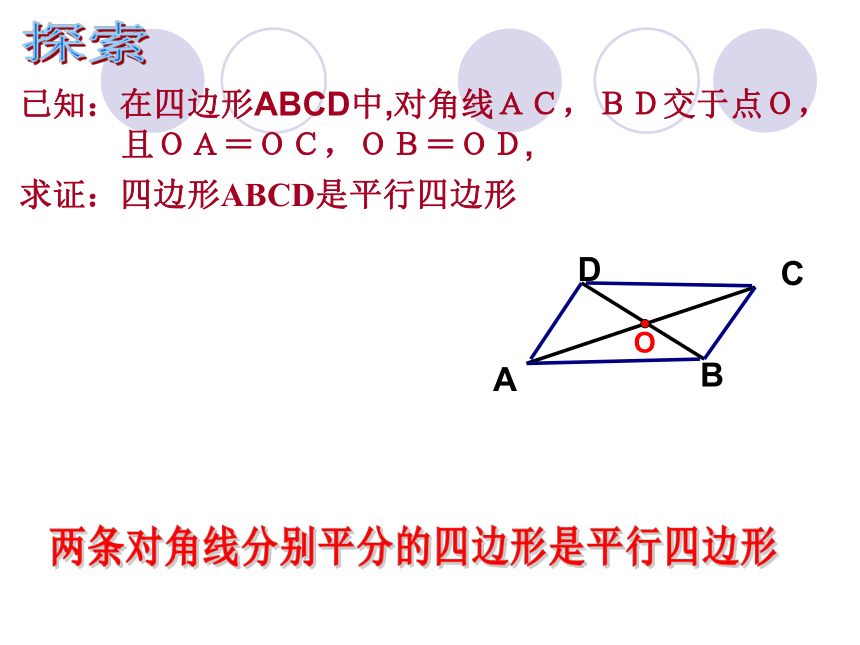
已知：在四边形ABCD中,对角线ＡＣ，ＢＤ交于点Ｏ，
且ＯＡ＝ＯＣ，ＯＢ＝ＯＤ,
求证：四边形ABCD是平行四边形
平行四边形判定定理4：
两条对角线互相平分的四边形是平行四边形.
几何语言：
∵OA=OC，OB=OD,
∴四边形ＡＢＣＤ是平行四边形
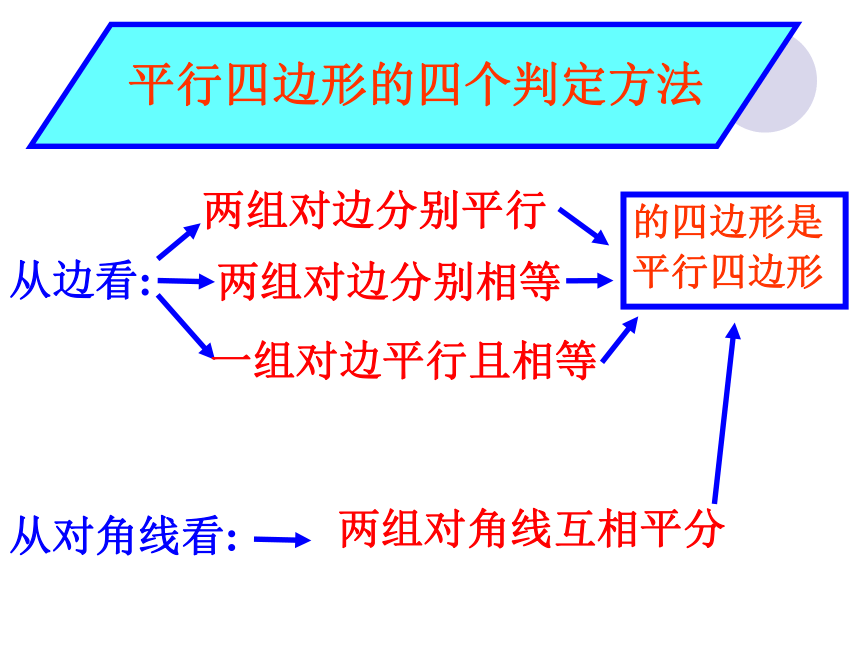
从边看:
平行四边形的四个判定方法
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形
从对角线看:
两组对角线互相平分
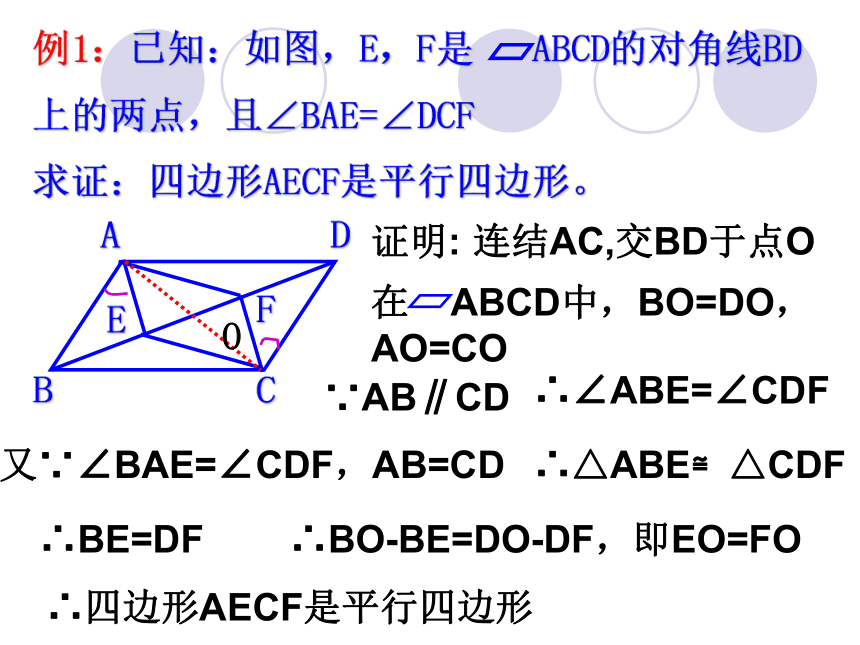
例1：已知：如图，E，F是 ABCD的对角线BD上的两点，且∠BAE=∠DCF 求证：四边形AECF是平行四边形。
A
B
C
D
E
F
O
证明:
连结AC,交BD于点O
∵AB∥CD
在 ABCD中，BO=DO，
AO=CO
∴∠ABE=∠CDF
又∵∠BAE=∠CDF，AB=CD
∴△ABE≌△CDF
∴BE=DF
∴BO-BE=DO-DF，即EO=FO
∴四边形AECF是平行四边形
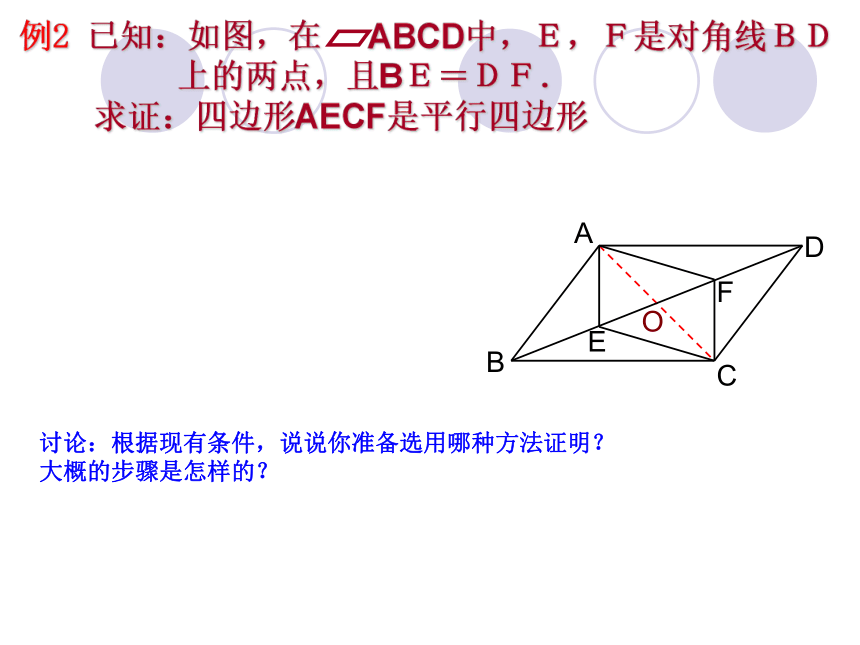
例2 已知：如图，在 ABCD中，Ｅ，Ｆ是对角线ＢＤ
上的两点，且BＥ＝ＤＦ．
求证：四边形AECF是平行四边形
F
E
D
C
B
A
O
讨论：根据现有条件，说说你准备选用哪种方法证明？
大概的步骤是怎样的？
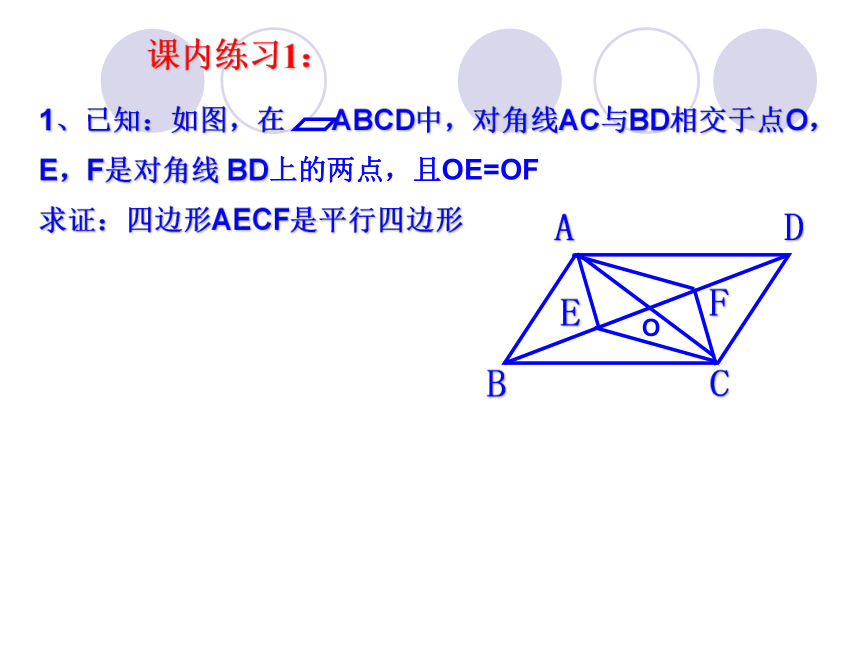
1、已知：如图，在 ABCD中，对角线AC与BD相交于点O，E，F是对角线 BD上的两点，且OE=OF 求证：四边形AECF是平行四边形
A
B
C
D
E
F
O
课内练习1：
2、如图，在 ABCD中，E，F是对角线AC上的两个点；G， H是对角线BD上的两个点，已知AE=CF，DG=BH，
求证：四边形EHFG是平行四边形
D
A
B
C
O
E
G
F
H
课内练习2：
证明：
在　　ＡＢＣＤ中，
ＯＡ＝ＯＣ，ＯＢ＝ＯＤ
∵ＡＥ＝ＣＦ，ＤＧ＝ＢＨ
∴ＯＥ＝ＯＦ，ＯＧ＝ＯＨ
∴四边形EHFG是平行四边形
如图
四边形ABCD是不是平行四边形？请给出证明.
A
B
C
D
x
y
o
-1
-1
1
1
∴Ｏ平分ＡＣ，Ｏ平分ＢＤ
连接对角线ＡＣ，ＢＤ则有
ＯＡ＝ＯＣ，ＯＢ＝ＯＤ
∴四边形ＡＢＣＤ是平行四边形
课内练习3：
已知线段a，b，∠α（如图），请用直尺和圆规作一个平行四边形，使它的两条对角线长分别等于线段a，b，两条对角线的夹角等于∠α
A
B
C
D
O
α
课内练习4：
探究活动
任意画一个三角形和三角形一边上的中线。比较这条中线的二倍与三角形另外两边的和的大小，你发现了什么 再画几个三角形试一试，你发现的规律仍然成立吗 试证明你的发现。
发现：三角形一条边上的中线的2倍小于另两条边的和。
E
已知：如图，AD是⊿ABC的中线，
求证：2AD证明：
如图，延长AD至E,使ED=AD.连结BE,EC.
∵BD=CD,
∴四边形ABEC是平行四边形（对角线互相平分的四边形是平行四边形）。
∴AB=CE(平行四边形的两组对边分别相等)。
∵AC+CE>AE,
∴AB+AC>2AD,
即2ADD
C
B
A
见中线延长一倍
通过今天的学习
你有哪些收获？
还存在哪些疑问？
从边看:
平行四边形的四个判定方法
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形
从对角线看:
两组对角线互相平分
平行四边形的性质定理和判定定理
条 件 结 论
性质
定理
判定
定理
1
四边形是平行四边形
两组对边平行且相等
四边形是平行四边形
对角线互相平分
2
1
2
3
四边形是平行四边形
四边形是平行四边形
四边形是平行四边形
两组对边分别相等
对角线互相平分
一组对边平行并且相等
布置作业:
1、复习、整理、巩固今天所学知识,
2、作业本(2).5.5 (1)基础练习必做，希望完成综合运用.
3、课课练A5.5 (1)课后作业必做,
当堂训练选做.
4.预习下一节课
思考:B.从角上考虑,如何判定平行四边形
两组对角分别相等的四边形是平行四边形.
D
A
C
B
方法5:推论1
已知：如图，四边形ABCD中, ∠A=∠C, ∠B=∠D.
求证：四边形ABCD是平行四边形。
证明: 在四边形ABCD中,
∵ ∠A=∠C, ∠B=∠D.
∴ ∠A+ ∠B=∠C+∠D.
∵∠A+ ∠B+∠C+∠D=360°.
∴ ∠A+ ∠B=∠C+∠D=180°,
∴ AD∥BC,
同理可得 AB∥CD,
∴四边形ABCD是平行四边形。
(两组对边分别平行的四边形是平行四边形)
思考:C.从边和角上共同考虑,如何判定平行四边形
有一组对边平行,一组对角相等的四边形是平行四边形.
D
A
C
B
方法6:推论2
已知：如图，四边形ABCD中, ∠A=∠C, AD∥CB.
求证：四边形ABCD是平行四边形。
证明: ∵ AD∥CB,
∴ ∠A+ ∠B=180°.
∴ ∠A=∠C,
∴∠C+∠B=180°,
∴ AB∥DC,
∴四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
还可以从哪个方向考虑呢
5.5 平行四边形的判定（2）