5.6三角形的中位线

(共11张PPT)
①把这四个全等三角形
拼成一个大的三角形
③这个三角形中有几个平行四边形，
你是怎么判断的？
②有没有相等的边和角？
④三角形内部的线段和三角形的边长
有何关系？
A
C
B
D
E
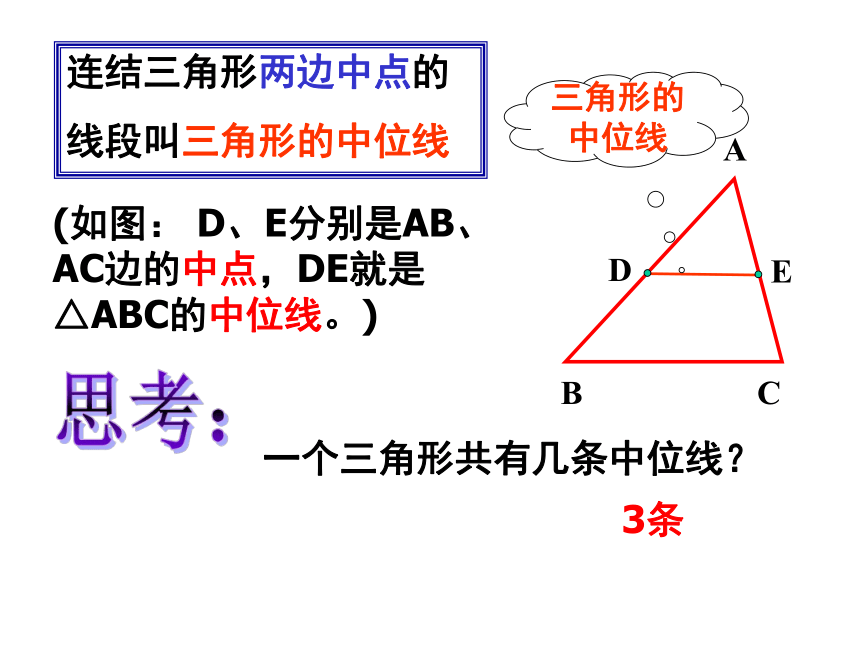
连结三角形两边中点的
线段叫三角形的中位线
(如图： D、E分别是AB、AC边的中点，DE就是△ABC的中位线。)
三角形的中位线
一个三角形共有几条中位线？
3条
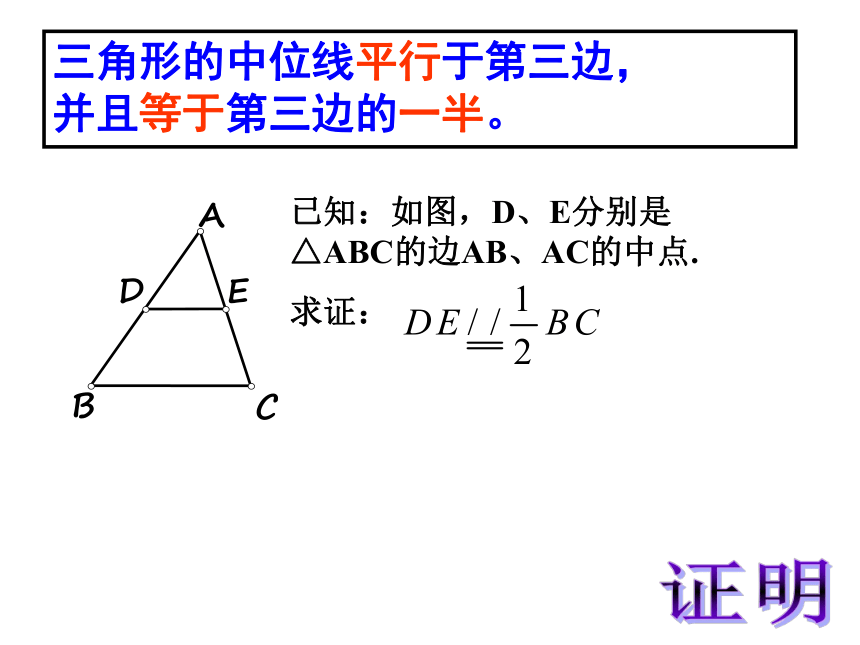
已知：如图，D、E分别是△ABC的边AB、AC的中点.
求证：
C
E
D
B
A
三角形的中位线平行于第三边，
并且等于第三边的一半。
C
E
D
F
B
A
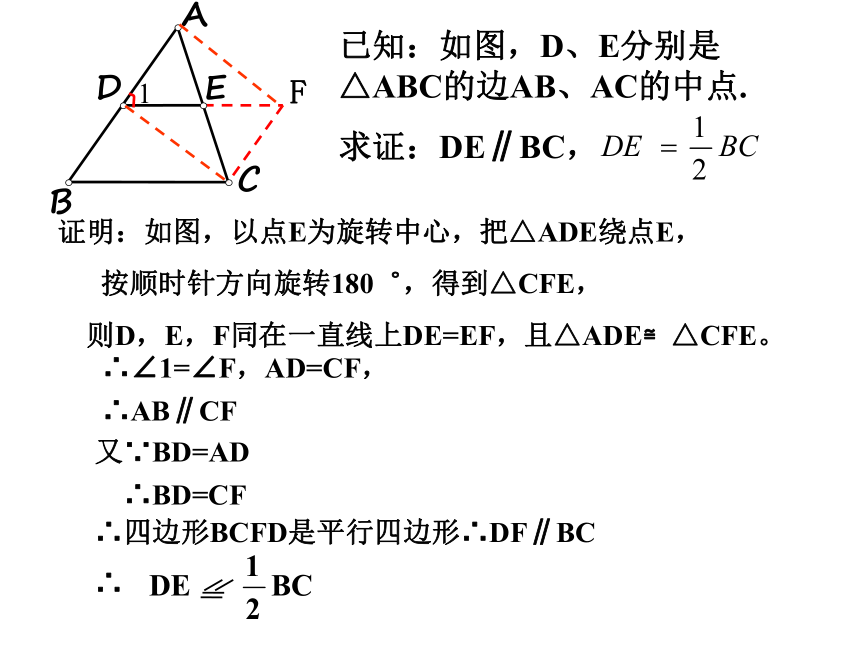
证明：如图，以点E为旋转中心，把△ADE绕点E，
按顺时针方向旋转180゜，得到△CFE，
则D，E，F同在一直线上DE=EF，且△ADE≌△CFE。
∴
已知：如图，D、E分别是△ABC的边AB、AC的中点.
求证：DE∥BC，
∴∠1=∠F，AD=CF，
∴AB∥CF
又∵BD=AD
∴四边形BCFD是平行四边形∴DF∥BC
1
∴BD=CF
　　三角形的中位线平行于第三边，并且等于第三边的一半.
几何语言：
∵DE是△ABC的中位线
∴DE∥BC,且DE= BC
C
E
D
B
A
B
D
A
E
C
F
(1) △DEF的周长与 △ABC的周长有什么关系
(2) 设△ABC的面积为S，则△DEF的面积=
△DEF的周长是 △ABC周长的一半
如图，
作出△ABC的3条中位线
DE，DF，EF
(3) 过D作DG⊥BC，垂足为G，过E作EH⊥BC，
垂足为H，则四边形DEHG的面积=
G
H
已知：如图，在四边形ABCD中，E、F、G、H分别是 AB、BC、CD、DA的中点.
①求证：四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
顺次连接四边形各边中点的线段组成
一个平行四边形
②若四边形ABCD的面积为10
求四边形EFGH的面积
如图,DE是△ABC的中位线,AF是BC边上的中线,DE和AF交于点O.
求证:DE与AF互相平分
F
E
D
C
B
A
O
已知：如图，△ABC是锐角三角形。分别以AB，AC为边向外侧作等边三角形ABM和等边三角形CAN。D，E，F分别是MB，BC，CN的中点，连结DE，EF。
A
B
C
D
E
F
N
M
求证：DE=EF
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线
① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
用 途