数学广场——位置的表示方法 课件(18张PPT)
文档属性
| 名称 | 数学广场——位置的表示方法 课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-22 18:45:56 | ||
图片预览



文档简介
早在300多年以前,法国著名的数学家笛卡尔就在反复思考一个问题:用什么办法,才能将“点”和“数”联系起来呢?突然,一只蜘蛛的“表演”让笛卡尔豁然开朗。他想,可以把蜘蛛看做一个点,蜘蛛的每个位置就能用一组数确定下来。于是在蜘蛛的启示下,笛卡尔用一对有顺序的数(x,y)表示平面上的一个点,创建了“数对”。
下面我们一起来认识数对,例如(左图)这两个点的位置可以怎样用数对表示呢?
A点的位置是第2列,第3行,就规定可以用数对(2 ,3)来表示。B点的位置是第5列,第6行,则用数对(5 ,6)来表示。就这样,后来我们用数对统一了位置的表示方法。同学们,你们能看懂吗?
第6行
第5行
第4行
第1行
第3行
第2行
0
第1列
第2列
第4列
第3列
第5列
B
A
第1列 第2列 第3列 第4列 第5列
第4行
第3行
第2行
第1行
超级秋千
旋转木马
碰碰车
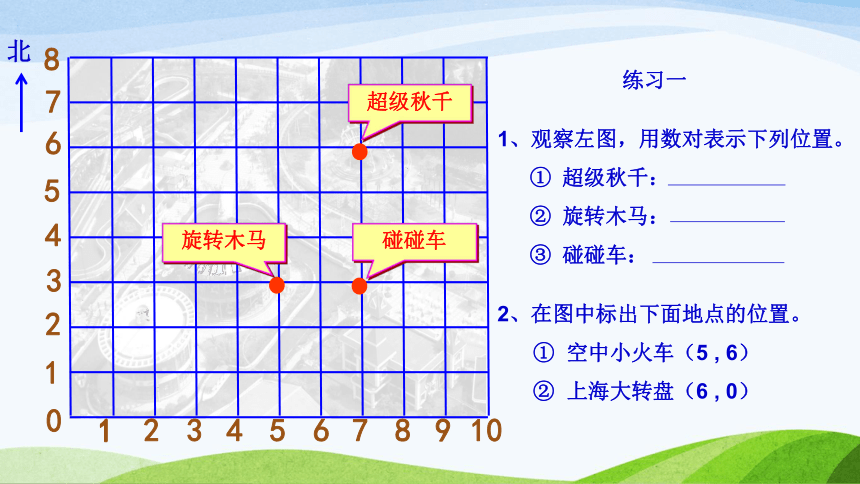
练习一
1、观察左图,用数对表示下列位置。
① 超级秋千:
② 旋转木马:
③ 碰碰车:
2、在图中标出下面地点的位置。
① 空中小火车(5 , 6)
② 上海大转盘(6 , 0)
10
北
1
2
3
4
5
6
7
8
9
1
0
1
2
3
7
6
5
4
8
超级秋千
碰碰车
旋转木马
1
2
3
4
5
6
7
8
9
10
1
0
1
2
3
7
6
5
4
8
北
(7,6)
(7,3)
(5,6)
(5,3)
(6,0)
练习二:猜一猜
A(2 ,5)
B(2 ,3)
C(4 ,3)
0
1
2
3
4
5
6
7
8
9
10
1
2
3
7
6
5
4
8
C(4,3)
B(2,3)
A(2,5)
回顾:
展望:
1
2
3
4
5
6
7
8
9
10
1
0
1
2
3
7
6
5
4
8
将练习二中三角形的每个点,按下面三种情况描点连线画出来,看看你有什么发现?
1、第一个数扩大到它的2倍,第二个数不变。
2、第一个数不变,第二个数扩大到它的2倍。
3、两个数同时扩大到它的2倍。
课后练习
Thank you.
Have a good time!
下面我们一起来认识数对,例如(左图)这两个点的位置可以怎样用数对表示呢?
A点的位置是第2列,第3行,就规定可以用数对(2 ,3)来表示。B点的位置是第5列,第6行,则用数对(5 ,6)来表示。就这样,后来我们用数对统一了位置的表示方法。同学们,你们能看懂吗?
第6行
第5行
第4行
第1行
第3行
第2行
0
第1列
第2列
第4列
第3列
第5列
B
A
第1列 第2列 第3列 第4列 第5列
第4行
第3行
第2行
第1行
超级秋千
旋转木马
碰碰车
练习一
1、观察左图,用数对表示下列位置。
① 超级秋千:
② 旋转木马:
③ 碰碰车:
2、在图中标出下面地点的位置。
① 空中小火车(5 , 6)
② 上海大转盘(6 , 0)
10
北
1
2
3
4
5
6
7
8
9
1
0
1
2
3
7
6
5
4
8
超级秋千
碰碰车
旋转木马
1
2
3
4
5
6
7
8
9
10
1
0
1
2
3
7
6
5
4
8
北
(7,6)
(7,3)
(5,6)
(5,3)
(6,0)
练习二:猜一猜
A(2 ,5)
B(2 ,3)
C(4 ,3)
0
1
2
3
4
5
6
7
8
9
10
1
2
3
7
6
5
4
8
C(4,3)
B(2,3)
A(2,5)
回顾:
展望:
1
2
3
4
5
6
7
8
9
10
1
0
1
2
3
7
6
5
4
8
将练习二中三角形的每个点,按下面三种情况描点连线画出来,看看你有什么发现?
1、第一个数扩大到它的2倍,第二个数不变。
2、第一个数不变,第二个数扩大到它的2倍。
3、两个数同时扩大到它的2倍。
课后练习
Thank you.
Have a good time!
