2.7 直角三角形的判定
图片预览



文档简介
(共12张PPT)
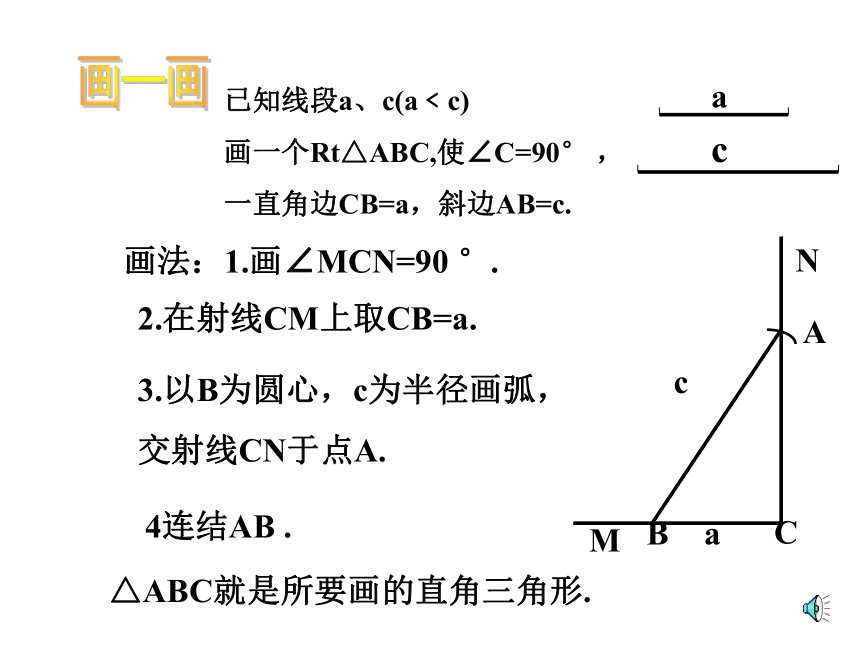
已知线段a、c(a﹤c)
画一个Rt△ABC,使∠C=90° ,
一直角边CB=a,斜边AB=c.
a
c
画法:1.画∠MCN=90 °.
3.以B为圆心,c为半径画弧,
交射线CN于点A.
4连结AB .
△ABC就是所要画的直角三角形.
M
C
N
a
B
c
A
2.在射线CM上取CB=a.
斜边、直角边公理
有斜边和一条直角边对应相等的两个三角形全等(可以简写成“斜边、直角边”或“HL”)
从上面画直角三角形中,你发现了什么?
斜边与一条直角边长一定时,所画的直角三角形
就是唯一的。
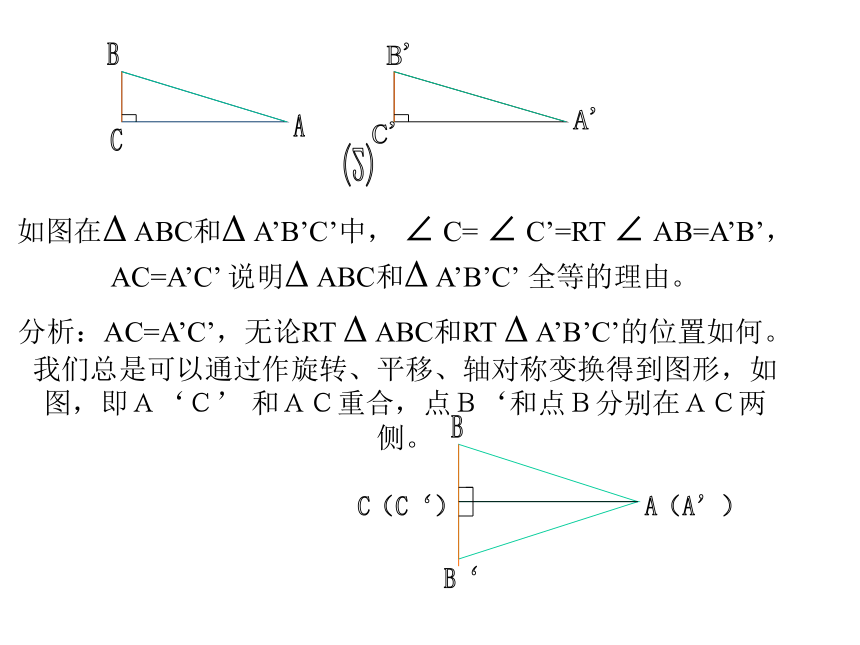
如图在Δ ABC和Δ A’B’C’中, ∠ C= ∠ C’=RT ∠ AB=A’B’,AC=A’C’ 说明Δ ABC和Δ A’B’C’ 全等的理由。
分析:AC=A’C’,无论RT Δ ABC和RT Δ A’B’C’的位置如何。我们总是可以通过作旋转、平移、轴对称变换得到图形,如图,即A‘C’ 和AC重合,点B‘和点B分别在AC两侧。
解∵ ∠ 1= ∠ 2=90 °
∴ BCB’在同一直线上,AC ┴ BB’
∵ AB=A’B’
∴ BC=B’C’(等腰三角形三线合一)
∵ AC=A’C’(公共边)
∴ RTΔABC ≌ RTΔA’B’C’(SSS)
(你还有其他方法吗?)
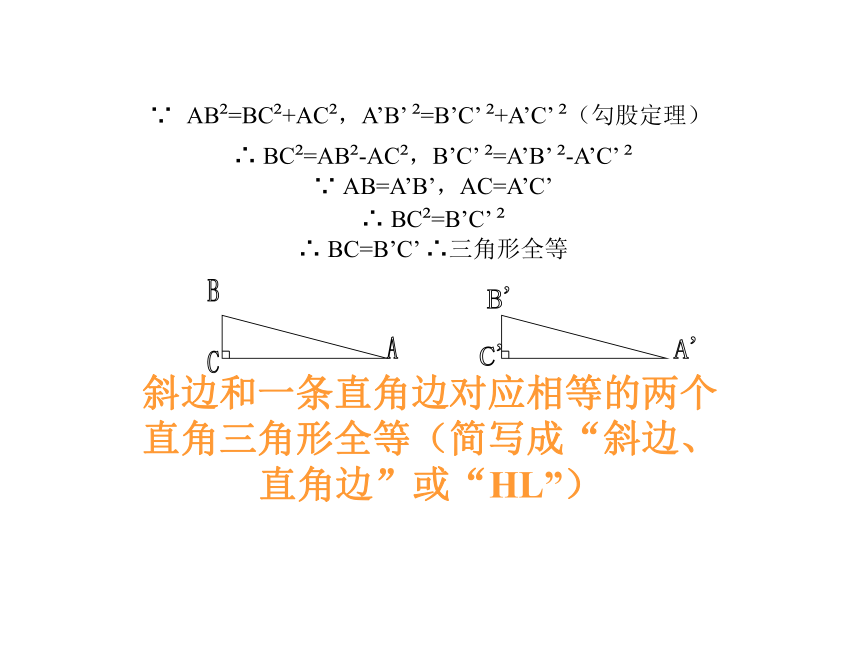
∵ AB =BC +AC ,A’B’ =B’C’ +A’C’ (勾股定理)
∴ BC =AB -AC ,B’C’ =A’B’ -A’C’
∵ AB=A’B’,AC=A’C’
∴ BC =B’C’
∴ BC=B’C’ ∴三角形全等
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)
例:已知P是∠ AOB内部一点,PD ┴ OA,PE ┴ OB
D,E分别是垂足,且PD=PE,则点P在∠ AOB的平分线上。请说明理由。
解作射线OP
∵ PD ┴ OA,PE ┴ OB,
∴ ∠ PDO= ∠ PEO=RT ∠
∵又OP=OP,PD=PE
∴ RT Δ PDO ≌ RT Δ PEO(HL)
∴ ∠ 1= ∠ 2,即点P在∠ AOB的平分线上。
角的内部,到角的两边距离相等的点 ,在这个角的平分线上
练习1如图,在Δ ABC中,D是BC的中点,DE ┴ AB于E,DF ┴ AC于F,且DE=DF,则AB=AC。说明理由。
解∵ DE ┴ AB,DF ┴ AC(已知)
∴ ∠ BED= ∠ CFD=RT ∠ (垂直意义)
∵ DE=DF(已知)
∵ BD=CD(中点意义)
∴ RT Δ BDE ≌ RT Δ CDF(HL)
∴ ∠ B= ∠ C(全等三角形对应角相等)
∴ AB=AC(等角对等边)
练习2如图,已知CE ┴ AB,DF ┴ AB,AC=BD,AF=BE,则CE=DF。请说明理由。
解∵ CE ┴ AB,DF ┴ AC(已知)
∴ ∠ AEC= ∠ BFD=RT ∠
∵ AF=BE (已知)
即AE+EF=BF+EF
AE=BF
∵ AC=BD
∴ RT Δ ACE ≌ RT Δ BDF(HL)
∴ CE=DF(全等三角形对应边相等)
练习3
已知Δ ABC如图,请找出一点P,使它到三边距离都相等(要求作出图形,并保留作图痕迹)
如图∠C= ∠D=Rt ∠ ,要证明△ACB≌ △BDA ,
,应补充什么条件?把它们分别写出来。
A
B
C
D
小结
1直角三角形是特殊的三角形,所以不仅可以应用一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“HL”公理。
2角的内部,到角的两边距离相等的点 ,在这个角的平分线上)。
已知线段a、c(a﹤c)
画一个Rt△ABC,使∠C=90° ,
一直角边CB=a,斜边AB=c.
a
c
画法:1.画∠MCN=90 °.
3.以B为圆心,c为半径画弧,
交射线CN于点A.
4连结AB .
△ABC就是所要画的直角三角形.
M
C
N
a
B
c
A
2.在射线CM上取CB=a.
斜边、直角边公理
有斜边和一条直角边对应相等的两个三角形全等(可以简写成“斜边、直角边”或“HL”)
从上面画直角三角形中,你发现了什么?
斜边与一条直角边长一定时,所画的直角三角形
就是唯一的。
如图在Δ ABC和Δ A’B’C’中, ∠ C= ∠ C’=RT ∠ AB=A’B’,AC=A’C’ 说明Δ ABC和Δ A’B’C’ 全等的理由。
分析:AC=A’C’,无论RT Δ ABC和RT Δ A’B’C’的位置如何。我们总是可以通过作旋转、平移、轴对称变换得到图形,如图,即A‘C’ 和AC重合,点B‘和点B分别在AC两侧。
解∵ ∠ 1= ∠ 2=90 °
∴ BCB’在同一直线上,AC ┴ BB’
∵ AB=A’B’
∴ BC=B’C’(等腰三角形三线合一)
∵ AC=A’C’(公共边)
∴ RTΔABC ≌ RTΔA’B’C’(SSS)
(你还有其他方法吗?)
∵ AB =BC +AC ,A’B’ =B’C’ +A’C’ (勾股定理)
∴ BC =AB -AC ,B’C’ =A’B’ -A’C’
∵ AB=A’B’,AC=A’C’
∴ BC =B’C’
∴ BC=B’C’ ∴三角形全等
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)
例:已知P是∠ AOB内部一点,PD ┴ OA,PE ┴ OB
D,E分别是垂足,且PD=PE,则点P在∠ AOB的平分线上。请说明理由。
解作射线OP
∵ PD ┴ OA,PE ┴ OB,
∴ ∠ PDO= ∠ PEO=RT ∠
∵又OP=OP,PD=PE
∴ RT Δ PDO ≌ RT Δ PEO(HL)
∴ ∠ 1= ∠ 2,即点P在∠ AOB的平分线上。
角的内部,到角的两边距离相等的点 ,在这个角的平分线上
练习1如图,在Δ ABC中,D是BC的中点,DE ┴ AB于E,DF ┴ AC于F,且DE=DF,则AB=AC。说明理由。
解∵ DE ┴ AB,DF ┴ AC(已知)
∴ ∠ BED= ∠ CFD=RT ∠ (垂直意义)
∵ DE=DF(已知)
∵ BD=CD(中点意义)
∴ RT Δ BDE ≌ RT Δ CDF(HL)
∴ ∠ B= ∠ C(全等三角形对应角相等)
∴ AB=AC(等角对等边)
练习2如图,已知CE ┴ AB,DF ┴ AB,AC=BD,AF=BE,则CE=DF。请说明理由。
解∵ CE ┴ AB,DF ┴ AC(已知)
∴ ∠ AEC= ∠ BFD=RT ∠
∵ AF=BE (已知)
即AE+EF=BF+EF
AE=BF
∵ AC=BD
∴ RT Δ ACE ≌ RT Δ BDF(HL)
∴ CE=DF(全等三角形对应边相等)
练习3
已知Δ ABC如图,请找出一点P,使它到三边距离都相等(要求作出图形,并保留作图痕迹)
如图∠C= ∠D=Rt ∠ ,要证明△ACB≌ △BDA ,
,应补充什么条件?把它们分别写出来。
A
B
C
D
小结
1直角三角形是特殊的三角形,所以不仅可以应用一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“HL”公理。
2角的内部,到角的两边距离相等的点 ,在这个角的平分线上)。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
