2直角三角形及勾股定理复习

(共9张PPT)
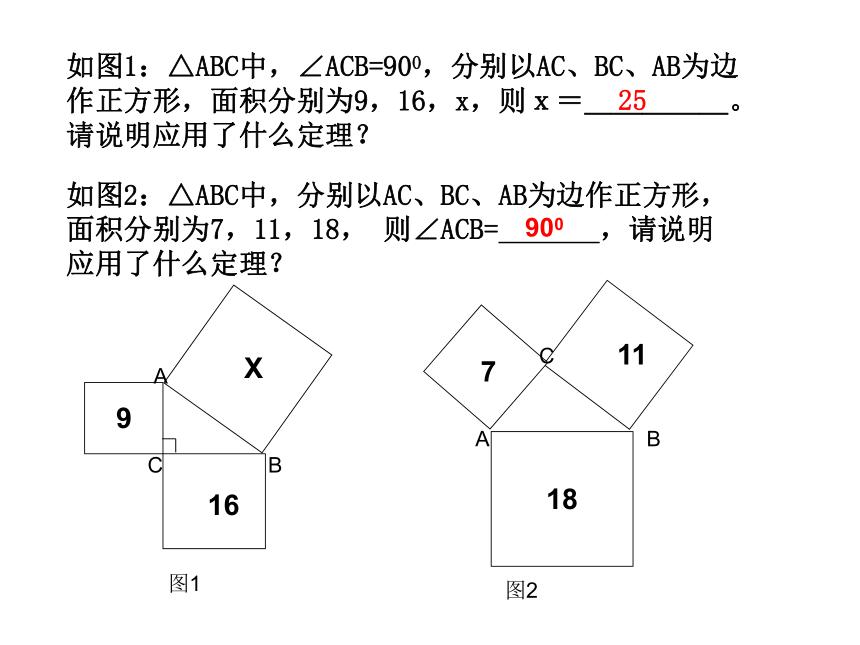
如图1：△ABC中，∠ACB=900，分别以AC、BC、AB为边作正方形，面积分别为9，16，x，则ｘ＝＿＿＿＿＿。请说明应用了什么定理？
如图2：△ABC中，分别以AC、BC、AB为边作正方形，面积分别为7，11，18， 则∠ACB= ，请说明应用了什么定理？
9
16
X
A
B
C
图1
18
7
11
A
C
B
图2
25
900
直角三角形及勾股定理复习
C
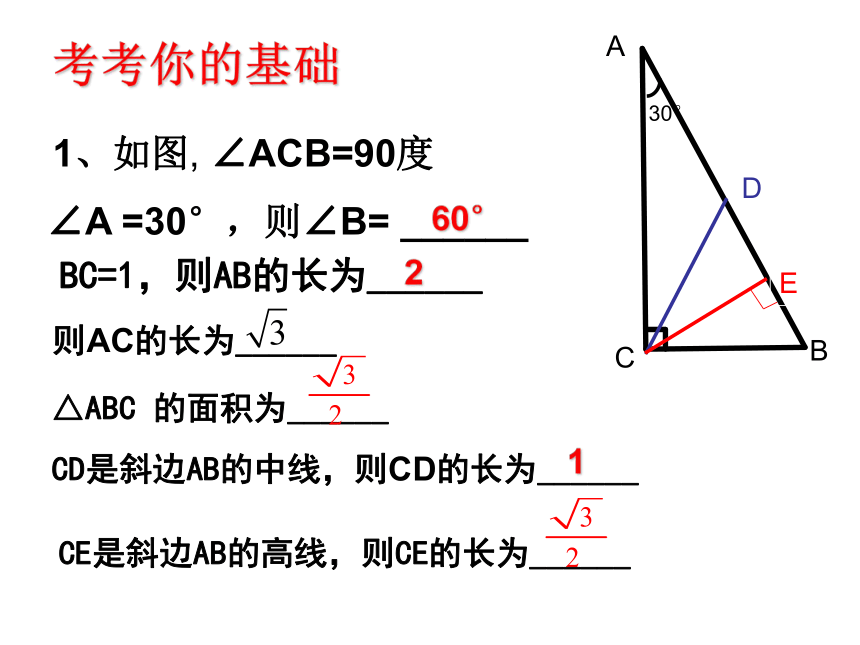
1、如图, ∠ACB=90度
∠A =30°，则∠B= ______
BC=1，则AB的长为______
则AC的长为______
　　
考考你的基础
30°
A
B
CD是斜边AB的中线，则CD的长为______
D
CE是斜边AB的高线，则CE的长为______
E
60°
2
1
△ABC 的面积为______
2、有四个三角形，分别满足下列条件：
一个内角等于另外两个内角之和；
(2) 三个内角之比为3∶4∶5；
(3) 三边分别为5、12、13；
(4) 一边上的中线等于这条边的一半；
其中直角三角形有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
C
例1、如图，四边形ABCD中，BA⊥DA，
BA＝DA＝2　　，DC＝3，BC＝5，
求∠ADC的度数
B
D
C
A
例2、如图，长方形纸片ABCD，沿着图中虚线折叠长方形的一边AD，使点D落在BC边的点F处，已知AB＝6ｃｍ，BC＝10ｃｍ，求EC的长。
A
D
E
C
F
B
6
10
如图，将长、宽分别为40cm，20cm的长方形纸片裁成两部分，
然后拼成一个直角三角形，
（1）如何裁，画出裁剪线；
（2）判断拼成三角形形状，并计算三角形各边长。
A
B
C
D
40
20
20
20
测测你的反应
10
10
2、已知一个三角形中，有两边长为7和24，要使三角形为直角三角形，则第三边为 。
1、如图，阴影部分（长方形）
的面积是＿＿＿＿
8
6
2
看看你的效果
3、在直角三角形中，若斜边与其中线之和为12，则斜边长为 ；
L
20
8
25
或
解：∵BC=5 CD=4 BD=3
∴BC2=CD2﹢BD2
∴ △BCD为Rt △
则 △ACD也为Rt △
设AD=x 则AB=x+BD=x+3 ∵AB=AC ∴AC=x+3
∴由勾股定理得（x+3）2 =x 2 +4 2 解得x=7/6
∴AB=7/6+3=25/6 ∴S △ ABC =25/6×4÷2=25/3
4、如图， △ ABC中，AB=AC，D是AB上一点，且BC=5，CD=4，BD=3，求△ ABC的面积。
5
4
3
x
x+3