4.5 “黄金分割”之黄金三角形 课件(共25张PPT)
文档属性
| 名称 | 4.5 “黄金分割”之黄金三角形 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-24 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
黄金分割之黄金三角形
浙教版
九年级
“黄金分割”欣赏
黄金分割一直被古希腊及历代建筑家、艺术家和雕塑家们所推崇,是美学和生命科学一个重要规律,数学中,它与勾股定理并称为几何中的“双宝”。蒙娜丽莎的美丽、天鹅芭蕾舞的优雅、优选法的运用、向日葵的规律排列,让黄金分割与艺术结缘,与科学联姻。百度引擎中关于“黄金分割”的中文网页就高达一千二百万篇。
其实有关“黄金分割”,我国也有记载。虽然没有古希腊的早,但它是我国古代数学家独立创造的,后来传入了印度。经考证,欧洲的比例算法是源于我国而经过印度由阿拉伯传入欧洲的,而不是直接从古希腊传入的。
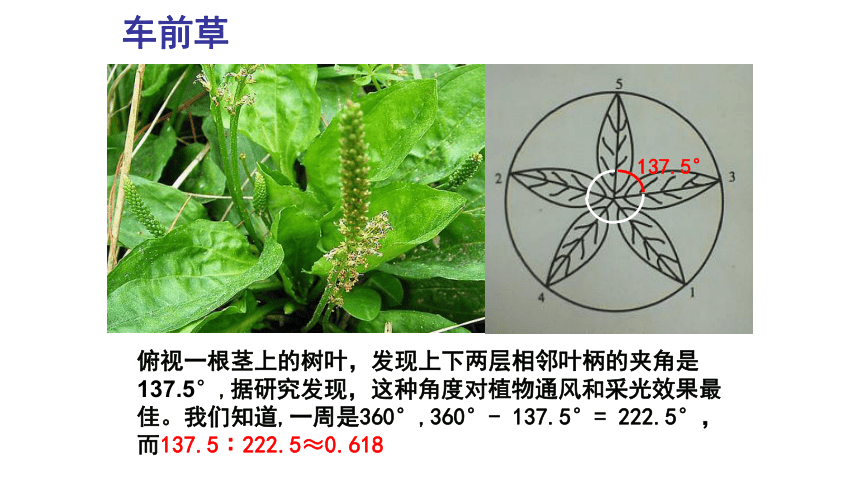
俯视一根茎上的树叶,发现上下两层相邻叶柄的夹角是137.5°,据研究发现,这种角度对植物通风和采光效果最佳。我们知道,一周是360°,360°-
137.5°=
222.5°,而137.5∶222.5≈0.618
137.5°
车前草
向日葵花有89个花瓣,55个朝一方,34个朝另一方,而34:55≈0.618
松果的秘密
8:13≈0.615
埃及胡夫金字塔,该塔高146米,底部正方形边长为232米,两者之比为146:232≈0.629
古希腊的帕特农神庙,其正立面的宽与长之比为19:31≈0.613
上海东方明珠塔高468米,上球体到地面的距离是289米,两者之比是289:468
≈0.618
468
289
埃菲尔铁塔,塔高为300米,二楼餐厅建于115米的半空,
(300-115)
300
115
二楼餐厅处于黄金分割点上(300-115):300≈0.617
维纳斯雕像
雅典娜女神雕像
肚脐处在人体总长度的黄金分割点
摄影
“黄金分割”之黄金三角形
古希腊数学家毕达哥拉斯有一句名言:“凡是美的东西,都有共同的特征,这就是部分与部分以及部分与整体之间的协调一致。”
毕达哥拉斯学派的标志
D
A
F
J
I
H
G
E
B
C
画法:
(1)五等分圆周
(2)依次隔一个点连接
著名特级教师易南轩
在研究名画《蒙娜丽莎》中,发现脸部存在“黄金三角形”
1.外鼻正面三角;
2.外鼻侧面三角;
3.鼻根点至两侧口角点组成的三角。
如图,在△ABC中,已知∠B=36°,BA=BC,
CD平分∠ACB.在直线AB或直线BC上是否存在点P(点A、B除外),使△PDC是黄金三角形?若存在,请在图中直接找出这样的点P;若不存在,请说明理由.
D
C
A
B
E
F
如图,在等腰△ABC中,顶角为36°,腰AB=1,底与腰之比为黄金比,设黄金比为k.其中△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,则第2011个黄金三角形的周长为(
)
A、k2010
B、k2011
C、k2010(2+k)
D、k2011(2+k)
G
定义
判定
性质
应用
基本图形
定义
判定
基本图形
性质
应用
黄金矩形
黄金三角形
小结:
黄金分割
课外作业:类比学习
黄金矩形
黄金矩形的定义、性质、判定、应用
建筑中的运用:古希腊的帕特农神庙
如果在一个黄金矩形里面画一个正方形,那么留下的矩形还是黄金矩形吗?
海螺
等角螺线
如果最大黄金矩形的长为1,则这条黄金螺线长为多少?
(黄金螺线)
谢谢指导
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
黄金分割之黄金三角形
浙教版
九年级
“黄金分割”欣赏
黄金分割一直被古希腊及历代建筑家、艺术家和雕塑家们所推崇,是美学和生命科学一个重要规律,数学中,它与勾股定理并称为几何中的“双宝”。蒙娜丽莎的美丽、天鹅芭蕾舞的优雅、优选法的运用、向日葵的规律排列,让黄金分割与艺术结缘,与科学联姻。百度引擎中关于“黄金分割”的中文网页就高达一千二百万篇。
其实有关“黄金分割”,我国也有记载。虽然没有古希腊的早,但它是我国古代数学家独立创造的,后来传入了印度。经考证,欧洲的比例算法是源于我国而经过印度由阿拉伯传入欧洲的,而不是直接从古希腊传入的。
俯视一根茎上的树叶,发现上下两层相邻叶柄的夹角是137.5°,据研究发现,这种角度对植物通风和采光效果最佳。我们知道,一周是360°,360°-
137.5°=
222.5°,而137.5∶222.5≈0.618
137.5°
车前草
向日葵花有89个花瓣,55个朝一方,34个朝另一方,而34:55≈0.618
松果的秘密
8:13≈0.615
埃及胡夫金字塔,该塔高146米,底部正方形边长为232米,两者之比为146:232≈0.629
古希腊的帕特农神庙,其正立面的宽与长之比为19:31≈0.613
上海东方明珠塔高468米,上球体到地面的距离是289米,两者之比是289:468
≈0.618
468
289
埃菲尔铁塔,塔高为300米,二楼餐厅建于115米的半空,
(300-115)
300
115
二楼餐厅处于黄金分割点上(300-115):300≈0.617
维纳斯雕像
雅典娜女神雕像
肚脐处在人体总长度的黄金分割点
摄影
“黄金分割”之黄金三角形
古希腊数学家毕达哥拉斯有一句名言:“凡是美的东西,都有共同的特征,这就是部分与部分以及部分与整体之间的协调一致。”
毕达哥拉斯学派的标志
D
A
F
J
I
H
G
E
B
C
画法:
(1)五等分圆周
(2)依次隔一个点连接
著名特级教师易南轩
在研究名画《蒙娜丽莎》中,发现脸部存在“黄金三角形”
1.外鼻正面三角;
2.外鼻侧面三角;
3.鼻根点至两侧口角点组成的三角。
如图,在△ABC中,已知∠B=36°,BA=BC,
CD平分∠ACB.在直线AB或直线BC上是否存在点P(点A、B除外),使△PDC是黄金三角形?若存在,请在图中直接找出这样的点P;若不存在,请说明理由.
D
C
A
B
E
F
如图,在等腰△ABC中,顶角为36°,腰AB=1,底与腰之比为黄金比,设黄金比为k.其中△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,则第2011个黄金三角形的周长为(
)
A、k2010
B、k2011
C、k2010(2+k)
D、k2011(2+k)
G
定义
判定
性质
应用
基本图形
定义
判定
基本图形
性质
应用
黄金矩形
黄金三角形
小结:
黄金分割
课外作业:类比学习
黄金矩形
黄金矩形的定义、性质、判定、应用
建筑中的运用:古希腊的帕特农神庙
如果在一个黄金矩形里面画一个正方形,那么留下的矩形还是黄金矩形吗?
海螺
等角螺线
如果最大黄金矩形的长为1,则这条黄金螺线长为多少?
(黄金螺线)
谢谢指导
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
