浙教版数学七年级上册2.6有理数的混合运算 练习课件(共34张PPT)
文档属性
| 名称 | 浙教版数学七年级上册2.6有理数的混合运算 练习课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-30 14:39:05 | ||
图片预览


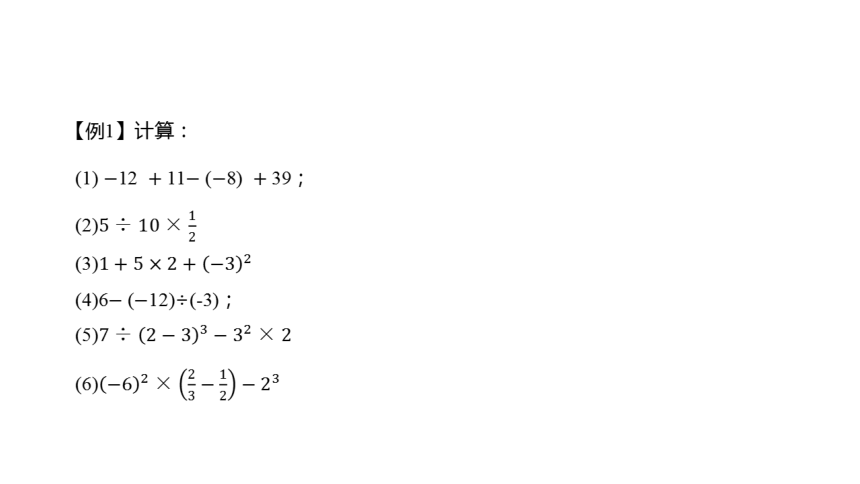







文档简介
(共34张PPT)
有理数的混合运算
我们学过的有理数的运算律:加法交换律:a+b=b+a;加法结合律:(a+b)+c=a+(b+c);乘法交换律:a×b=b×a;乘法结合律:(a×b)×c=a×(b×c);乘法分配律:a×(b+c)=a×b+a×c.复习回顾:
有理数的混合运算:
【例1】计算:
(1) 12 11(8) 39;
(2)
(3)
(4)6(12)÷(-3);
(5)
(6)
有理数的混合运算:
【例1】计算:
(1) 12 11(8) 39;
(2)
(3)
(4)6(12)÷(-3);
(5)
(6)
同 级 运 算,从 左 至 右
异 级 运 算,由 高 到 低
若 有 括 号,先 算 内 部
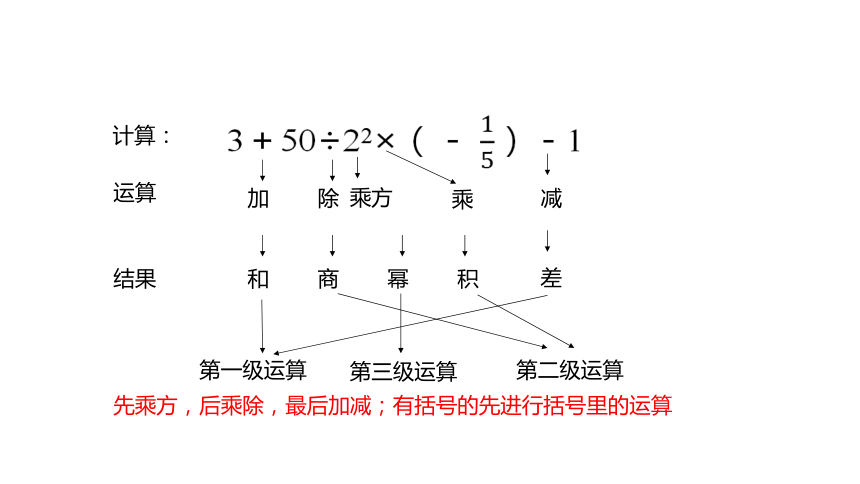
3+50÷22×(- )-1
计算:
加
除
乘方
乘
减
运算
结果
和
商
幂
积
差
第一级运算
第二级运算
第三级运算
先乘方,后乘除,最后加减;有括号的先进行括号里的运算
有理数的混合运算:
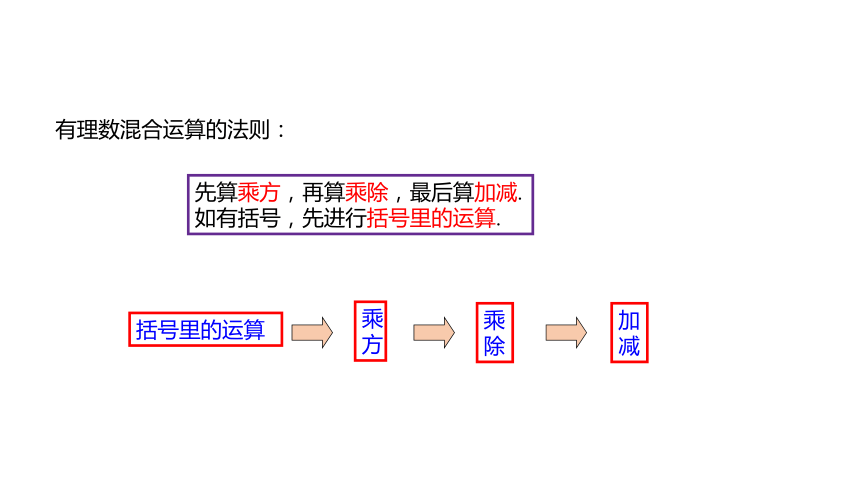
乘方
乘除
加减
括号里的运算
有理数混合运算的法则:
先算乘方,再算乘除,最后算加减.
如有括号,先进行括号里的运算.
方法归纳:
有理数的混合运算:
【例2】计算:
(1) (2)
注意:在计算前应该理清算式中含有哪几种运算,再考虑运算顺序,
同时计算的各项要同步表达,暂不计算的项应照抄,不要遗漏。
同级运算应按从左到右的顺序计算.
有理数的混合运算:
;
【练2-1】做一做:
【练2-2】比较大小:(1)32+42____52;
(2)(-3)2+42____2×(-3)×4;
(3)-|-2|____-(-2)3.
【练2-3】设a=-2×42,b=-(2×4)2,c=-(2-4)2,则a,b,c的大小关系为( )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
有理数的混合运算:
【练2-2】比较大小:(1)32+42____52;
(2)(-3)2+42____2×(-3)×4;
(3)-|-2|____-(-2)3.
【练2-3】设a=-2×42,b=-(2×4)2,c=-(2-4)2,则a,b,c的大小关系为( B )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
=
>
<
解析:
【练2-4】下列计算对吗?如果不对,应如何改正?
有理数的混合运算:
【练2-5】计算:(1)(2)答案:0答案:(3)(4)答案:答案:-8解析:【练2-6】计算:
(1) (2)
(3)
解析:
答案:24.
答案:-3.
答案:33.
1.2
3
算式为:π×32-1.22
解:π×32-1.22
= 9×π-1.44
≈ 28.26-1.44
= 26.82(m2)
【例3】学校将建一圆形花坛,半径为3m,中间雕塑的底面是边长为1.2m的正方形(如图),你能用算式表示该花坛的实际种花面积吗 这个算式有哪几种运算 这个花坛的实际种花面积是多少 (π取3.14)
解析:
运算顺序:先乘方,后乘法,最后减法
解析:
【例4】半径是10cm,高为30cm的圆柱形水桶中装满了水。小明先将桶中的水倒满2个底面半径为3cm,高为5cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别为50cm,20cm和20cm的长方体容器内。长方体容器内水的高度大约是多少cm?(π取3,容器的厚度不计)
π×102×30
π×102×30- 2×π×32×5
2×π×32×5
50×20×?
解:水桶内水的体积π ×102×30 cm3,倒满2个杯子后,剩下的水的体积为(π ×102×30-2×π ×32×5)cm3.
(π ×102×30-2× π ×32×5)÷(50×20)=(9000-270)÷1000=8730÷1000=8.73(cm).
答:容器内水的高度约为8.73cm.
【练4】小明的爸爸在一家合资企业上班,月工资为5 600元.按规定,其中3 500元是免税的,其余部分需缴纳个人所得税.应纳税部分又要分成两部分,按不同税率纳税.不超过1 500元的部分的税率为3%;超过1 500元但不超过4 500元的部分的税率为10%,小明的爸爸每月要缴纳的个人所得税是多少元?解:1 500×3%+(5 600-3 500-1 500)×10%=105(元).答:小明的爸爸每月要缴纳的个人所得税是105元.解析:你能读出小明的身高吗?
155cm
150cm
160cm
观察与思考:
曾侯乙编钟是由64个青铜编钟组成,分3层排列,共8组,最大的高153.4厘米,最小的高20.2厘米,其造型壮观,配备齐全,音列齐全,音频准确,堪称中国古代编钟之最,经考古判断,该编钟是约2400年前春秋晚期的文物.
观察与思考:
准确数:如上面语段中,64这个数与青铜编钟的实际个数完全符合,这样的数称为
准确数.
近似数:像153.4,20.2,2400这三个数是通过测量或估计得到的,它们与编钟的实
际高度比较接近,但不完全符合。像这样的数与实际接近的数称为近似数.
近似数:
注意:通过测量或估计得到的都是近似数.
【例5】下列实际问题中出现的数,哪些是准确数,哪些是近似数?
(1)教室里有56名同学;
(2)小明的身高为1.57m;
(3)我国的国土面积大约是960万km ;
(4)月球和地球之间的平均距离大约是38万km;
(5)某本书的定价是4.50元;
近似数:
近似数:
我国人口总数为13亿
某词典共有1234页
客观条件无法得到或难以得到精确数据
有时实际问题中无需得到精确数据
某年级有97人,买门票大约需要800元
【练5】(1)上面的数据,哪些是准确数?哪些是近似数的?
(2)举例说明生活中那些数据是准确数?哪些数据是近似数?
请指出 9576.234 中每一个数的位置:
如:5位于百位
9位于 . 7位于 .
6位于 . 2位于 .
3位于 . 4位于 .
复习回顾:
请指出 9576.234 中每一个数的位置:
如:5位于百位
9位于千位 7位于十位
6位于个位 2位于十分位
3位于百分位 4位于千分位
复习回顾:
【例6】小明量得课桌长为1.025米,请按下列要求取这个数的近似数:
(1)四舍五入到百分位;
(1.03米)
(2)四舍五入到十分位;
(1.0米)
(3)四舍五入到个位。
(1米)
利用四舍五入法得到的近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.
解析:
3、近似数38万是精确到哪一位呢?
表示实际数据在什么范围内呢?
近似数38万是千位数字四舍五入到万位的结果,所以说它精确到万位,
表示实际数字大于或等于37.5万而小于38.5万
1、近似数1.57米是精确到哪一位呢?表示实际数据在什么范围内呢?
2、有2个小朋友他们身高的近似数都是1.6米,
请问他们身高有相差9cm的可能吗?
百分位 1.565~1.575米
可能
想一想:
有效数字:
有效数字:
由四舍五入得到的近似数,从左边第一个不是0 的数字起,到末位数字为止的所有数字都
叫做这个数的有效数字。
如:1.50有3个有效数字:1,5,0
0.0307有3个有效数字:3,0, 7
0.03070有4个有效数字:3,0,7,0
有效数字:
【例7】下列由四舍五入法得到近似数,各精确到哪一位,各有哪几个有效数字?
(1)11亿 (2)36.8 (3) 1.2万 (4) 1.20万
【例7】用四舍五入法,按括号内的要求对下列各数取近似值:
(1)0.33448(精确到千分位);
(2)1.5952(精确到0.01)
(3)0.05069(保留2个有效数字)
(4)84960(保留3个有效数字)
有效数字越多,精确度越大;近似数中越左边的数字就越重要.
解析:
【练7】下列由四舍五入法得到的近似数, 各精确到哪一位?有几个有效数字?
(1)132.4精确到______,有 __个有效数字,分别为_________。
十分位
4
1 , 3 , 2 , 4
万分位
3
5 , 7 , 2
千位
2
2 , 4
2 , 4
千位
2
(2) 0.0572精确到______,有 __个有效数字,分别为_________。
(3)2.4 万精确到______,有 __个有效数字,分别为__________。
(4)2.4×104精确到______,有 __个有效数字,分别为_______。
1.下列计算不正确的是()A.B.C.D.2.下列计算正确的是( )A.(-8)×÷(-)×4=-2÷(-1)=2B.-22+(8-10)2-4×(-2)2=4+4-16=-8C.(-6.25)×(-4)-135÷(-15)=25-9=16D.0-(-3)2÷3×(-2)3=0-9÷3×(-2)3=0-3×(-8)=24当堂检测:3.近似数4.70所表示的精确值x的取值范围是( )A.4.695≤x<4.705B.4.60≤x<4.80C.4.695<x≤4.705D.4.700<x≤4.7054.用四舍五入法对下列各数取近似数.(1)109.654(精确到十分位);(2)1.89972(精确到0.001);(3)13575084(精确到十万位);(4)230460(精确到千位).当堂检测:5.计算:(1)(2)(3)当堂检测:6.司机小王加满50 L的汽油后,从火车站出发,向东行驶32 km遇上一位要去火车站的客人,于是调头原路返回,行驶到一半的路程时,客人突然有事下车,此时小王在火车站什么位置?如果该汽车每100 km耗油10 L,问:到现在为止,小王的车里还剩下多少汽油?当堂检测:7.司机小王加满50 L的汽油后,从火车站出发,向东行驶32 km遇上一位要去火车站的客人,于是调头原路返回,行驶到一半的路程时,客人突然有事下车,此时小王在火车站什么位置?如果该汽车每100 km耗油10 L,问:到现在为止,小王的车里还剩下多少汽油?解析:
有理数的混合运算
我们学过的有理数的运算律:加法交换律:a+b=b+a;加法结合律:(a+b)+c=a+(b+c);乘法交换律:a×b=b×a;乘法结合律:(a×b)×c=a×(b×c);乘法分配律:a×(b+c)=a×b+a×c.复习回顾:
有理数的混合运算:
【例1】计算:
(1) 12 11(8) 39;
(2)
(3)
(4)6(12)÷(-3);
(5)
(6)
有理数的混合运算:
【例1】计算:
(1) 12 11(8) 39;
(2)
(3)
(4)6(12)÷(-3);
(5)
(6)
同 级 运 算,从 左 至 右
异 级 运 算,由 高 到 低
若 有 括 号,先 算 内 部
3+50÷22×(- )-1
计算:
加
除
乘方
乘
减
运算
结果
和
商
幂
积
差
第一级运算
第二级运算
第三级运算
先乘方,后乘除,最后加减;有括号的先进行括号里的运算
有理数的混合运算:
乘方
乘除
加减
括号里的运算
有理数混合运算的法则:
先算乘方,再算乘除,最后算加减.
如有括号,先进行括号里的运算.
方法归纳:
有理数的混合运算:
【例2】计算:
(1) (2)
注意:在计算前应该理清算式中含有哪几种运算,再考虑运算顺序,
同时计算的各项要同步表达,暂不计算的项应照抄,不要遗漏。
同级运算应按从左到右的顺序计算.
有理数的混合运算:
;
【练2-1】做一做:
【练2-2】比较大小:(1)32+42____52;
(2)(-3)2+42____2×(-3)×4;
(3)-|-2|____-(-2)3.
【练2-3】设a=-2×42,b=-(2×4)2,c=-(2-4)2,则a,b,c的大小关系为( )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
有理数的混合运算:
【练2-2】比较大小:(1)32+42____52;
(2)(-3)2+42____2×(-3)×4;
(3)-|-2|____-(-2)3.
【练2-3】设a=-2×42,b=-(2×4)2,c=-(2-4)2,则a,b,c的大小关系为( B )
A.a<b<c B.b<a<c C.c<b<a D.c<a<b
=
>
<
解析:
【练2-4】下列计算对吗?如果不对,应如何改正?
有理数的混合运算:
【练2-5】计算:(1)(2)答案:0答案:(3)(4)答案:答案:-8解析:【练2-6】计算:
(1) (2)
(3)
解析:
答案:24.
答案:-3.
答案:33.
1.2
3
算式为:π×32-1.22
解:π×32-1.22
= 9×π-1.44
≈ 28.26-1.44
= 26.82(m2)
【例3】学校将建一圆形花坛,半径为3m,中间雕塑的底面是边长为1.2m的正方形(如图),你能用算式表示该花坛的实际种花面积吗 这个算式有哪几种运算 这个花坛的实际种花面积是多少 (π取3.14)
解析:
运算顺序:先乘方,后乘法,最后减法
解析:
【例4】半径是10cm,高为30cm的圆柱形水桶中装满了水。小明先将桶中的水倒满2个底面半径为3cm,高为5cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别为50cm,20cm和20cm的长方体容器内。长方体容器内水的高度大约是多少cm?(π取3,容器的厚度不计)
π×102×30
π×102×30- 2×π×32×5
2×π×32×5
50×20×?
解:水桶内水的体积π ×102×30 cm3,倒满2个杯子后,剩下的水的体积为(π ×102×30-2×π ×32×5)cm3.
(π ×102×30-2× π ×32×5)÷(50×20)=(9000-270)÷1000=8730÷1000=8.73(cm).
答:容器内水的高度约为8.73cm.
【练4】小明的爸爸在一家合资企业上班,月工资为5 600元.按规定,其中3 500元是免税的,其余部分需缴纳个人所得税.应纳税部分又要分成两部分,按不同税率纳税.不超过1 500元的部分的税率为3%;超过1 500元但不超过4 500元的部分的税率为10%,小明的爸爸每月要缴纳的个人所得税是多少元?解:1 500×3%+(5 600-3 500-1 500)×10%=105(元).答:小明的爸爸每月要缴纳的个人所得税是105元.解析:你能读出小明的身高吗?
155cm
150cm
160cm
观察与思考:
曾侯乙编钟是由64个青铜编钟组成,分3层排列,共8组,最大的高153.4厘米,最小的高20.2厘米,其造型壮观,配备齐全,音列齐全,音频准确,堪称中国古代编钟之最,经考古判断,该编钟是约2400年前春秋晚期的文物.
观察与思考:
准确数:如上面语段中,64这个数与青铜编钟的实际个数完全符合,这样的数称为
准确数.
近似数:像153.4,20.2,2400这三个数是通过测量或估计得到的,它们与编钟的实
际高度比较接近,但不完全符合。像这样的数与实际接近的数称为近似数.
近似数:
注意:通过测量或估计得到的都是近似数.
【例5】下列实际问题中出现的数,哪些是准确数,哪些是近似数?
(1)教室里有56名同学;
(2)小明的身高为1.57m;
(3)我国的国土面积大约是960万km ;
(4)月球和地球之间的平均距离大约是38万km;
(5)某本书的定价是4.50元;
近似数:
近似数:
我国人口总数为13亿
某词典共有1234页
客观条件无法得到或难以得到精确数据
有时实际问题中无需得到精确数据
某年级有97人,买门票大约需要800元
【练5】(1)上面的数据,哪些是准确数?哪些是近似数的?
(2)举例说明生活中那些数据是准确数?哪些数据是近似数?
请指出 9576.234 中每一个数的位置:
如:5位于百位
9位于 . 7位于 .
6位于 . 2位于 .
3位于 . 4位于 .
复习回顾:
请指出 9576.234 中每一个数的位置:
如:5位于百位
9位于千位 7位于十位
6位于个位 2位于十分位
3位于百分位 4位于千分位
复习回顾:
【例6】小明量得课桌长为1.025米,请按下列要求取这个数的近似数:
(1)四舍五入到百分位;
(1.03米)
(2)四舍五入到十分位;
(1.0米)
(3)四舍五入到个位。
(1米)
利用四舍五入法得到的近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.
解析:
3、近似数38万是精确到哪一位呢?
表示实际数据在什么范围内呢?
近似数38万是千位数字四舍五入到万位的结果,所以说它精确到万位,
表示实际数字大于或等于37.5万而小于38.5万
1、近似数1.57米是精确到哪一位呢?表示实际数据在什么范围内呢?
2、有2个小朋友他们身高的近似数都是1.6米,
请问他们身高有相差9cm的可能吗?
百分位 1.565~1.575米
可能
想一想:
有效数字:
有效数字:
由四舍五入得到的近似数,从左边第一个不是0 的数字起,到末位数字为止的所有数字都
叫做这个数的有效数字。
如:1.50有3个有效数字:1,5,0
0.0307有3个有效数字:3,0, 7
0.03070有4个有效数字:3,0,7,0
有效数字:
【例7】下列由四舍五入法得到近似数,各精确到哪一位,各有哪几个有效数字?
(1)11亿 (2)36.8 (3) 1.2万 (4) 1.20万
【例7】用四舍五入法,按括号内的要求对下列各数取近似值:
(1)0.33448(精确到千分位);
(2)1.5952(精确到0.01)
(3)0.05069(保留2个有效数字)
(4)84960(保留3个有效数字)
有效数字越多,精确度越大;近似数中越左边的数字就越重要.
解析:
【练7】下列由四舍五入法得到的近似数, 各精确到哪一位?有几个有效数字?
(1)132.4精确到______,有 __个有效数字,分别为_________。
十分位
4
1 , 3 , 2 , 4
万分位
3
5 , 7 , 2
千位
2
2 , 4
2 , 4
千位
2
(2) 0.0572精确到______,有 __个有效数字,分别为_________。
(3)2.4 万精确到______,有 __个有效数字,分别为__________。
(4)2.4×104精确到______,有 __个有效数字,分别为_______。
1.下列计算不正确的是()A.B.C.D.2.下列计算正确的是( )A.(-8)×÷(-)×4=-2÷(-1)=2B.-22+(8-10)2-4×(-2)2=4+4-16=-8C.(-6.25)×(-4)-135÷(-15)=25-9=16D.0-(-3)2÷3×(-2)3=0-9÷3×(-2)3=0-3×(-8)=24当堂检测:3.近似数4.70所表示的精确值x的取值范围是( )A.4.695≤x<4.705B.4.60≤x<4.80C.4.695<x≤4.705D.4.700<x≤4.7054.用四舍五入法对下列各数取近似数.(1)109.654(精确到十分位);(2)1.89972(精确到0.001);(3)13575084(精确到十万位);(4)230460(精确到千位).当堂检测:5.计算:(1)(2)(3)当堂检测:6.司机小王加满50 L的汽油后,从火车站出发,向东行驶32 km遇上一位要去火车站的客人,于是调头原路返回,行驶到一半的路程时,客人突然有事下车,此时小王在火车站什么位置?如果该汽车每100 km耗油10 L,问:到现在为止,小王的车里还剩下多少汽油?当堂检测:7.司机小王加满50 L的汽油后,从火车站出发,向东行驶32 km遇上一位要去火车站的客人,于是调头原路返回,行驶到一半的路程时,客人突然有事下车,此时小王在火车站什么位置?如果该汽车每100 km耗油10 L,问:到现在为止,小王的车里还剩下多少汽油?解析:
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
