5.1 多边形(1)

(共26张PPT)
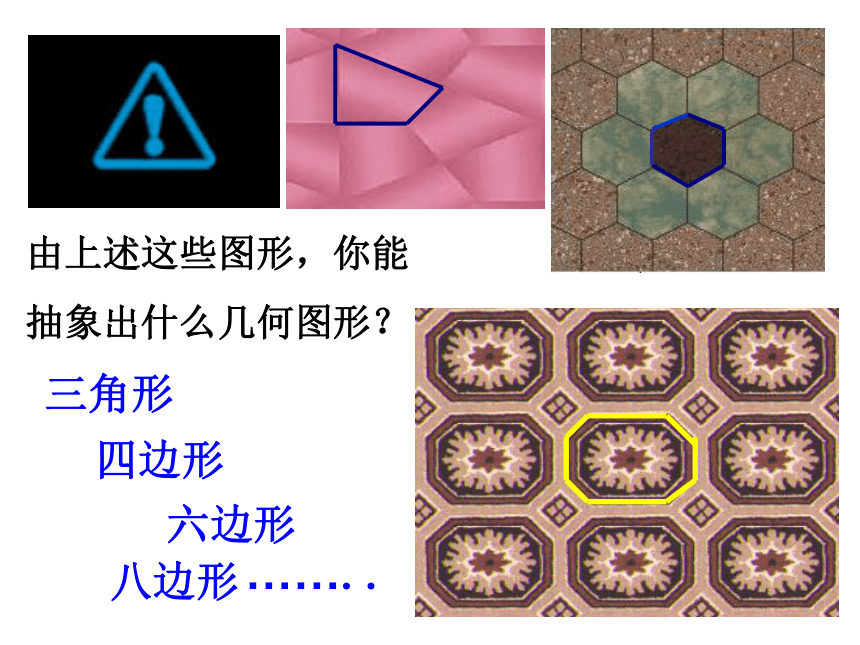
由上述这些图形，你能
抽象出什么几何图形？
三角形
四边形
六边形
八边形
……..
定义：
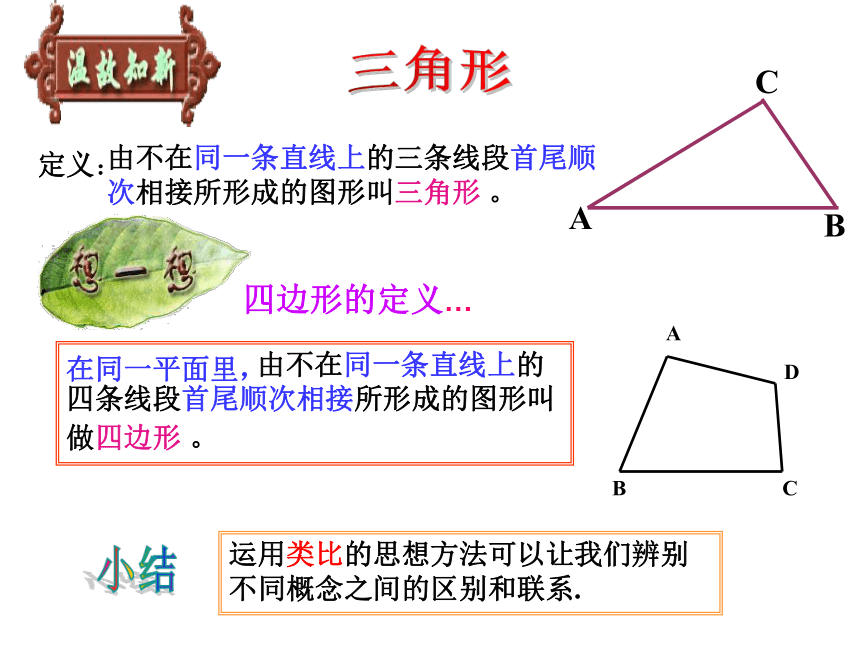
由不在同一条直线上的三条线段首尾顺次相接所形成的图形叫三角形 。
A
B
C
由不在同一条直线上的四条线段首尾顺次相接所形成的图形叫做四边形 。 　　　　　　
A
D
B C
四边形的定义…
在同一平面里，
运用类比的思想方法可以让我们辨别不同概念之间的区别和联系.
A
B
C
D
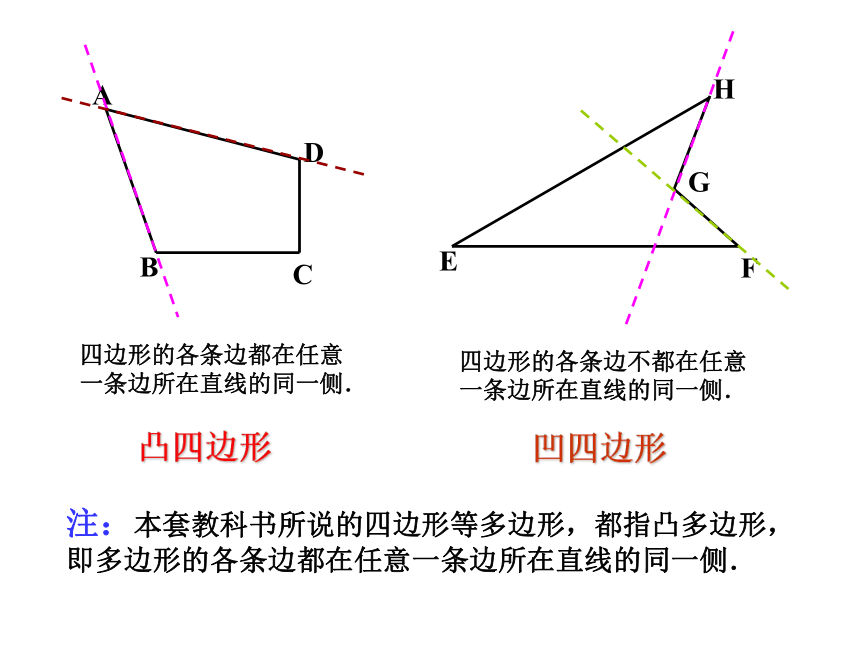
凸四边形
E
F
G
H
凹四边形
注：本套教科书所说的四边形等多边形，都指凸多边形，即多边形的各条边都在任意一条边所在直线的同一侧．
四边形的各条边都在任意　一条边所在直线的同一侧．
四边形的各条边不都在任意一条边所在直线的同一侧．
A
B
C
D
顶点
内角
边
对角线
外角
E
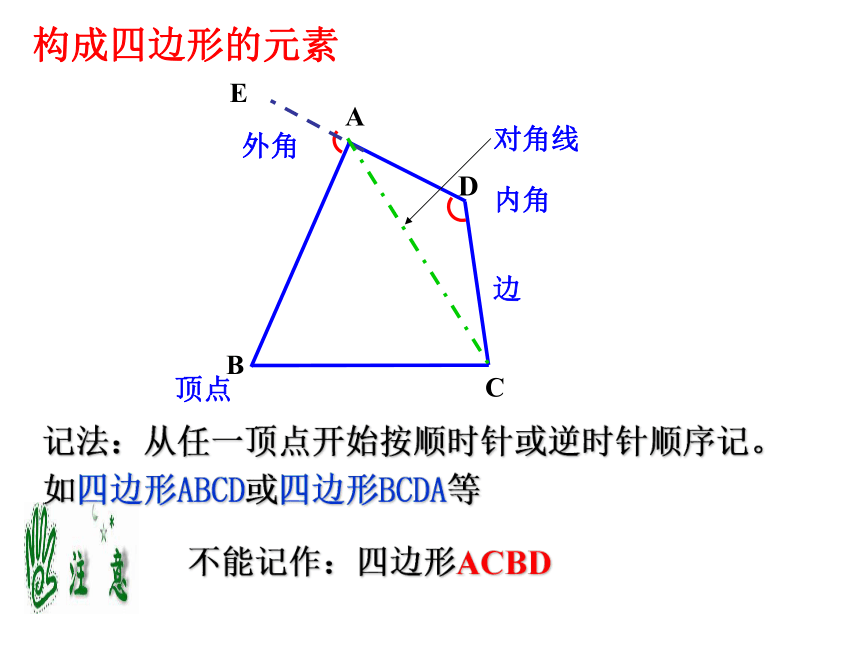
构成四边形的元素
不能记作：四边形ACBD
记法：从任一顶点开始按顺时针或逆时针顺序记。如四边形ABCD或四边形BCDA等
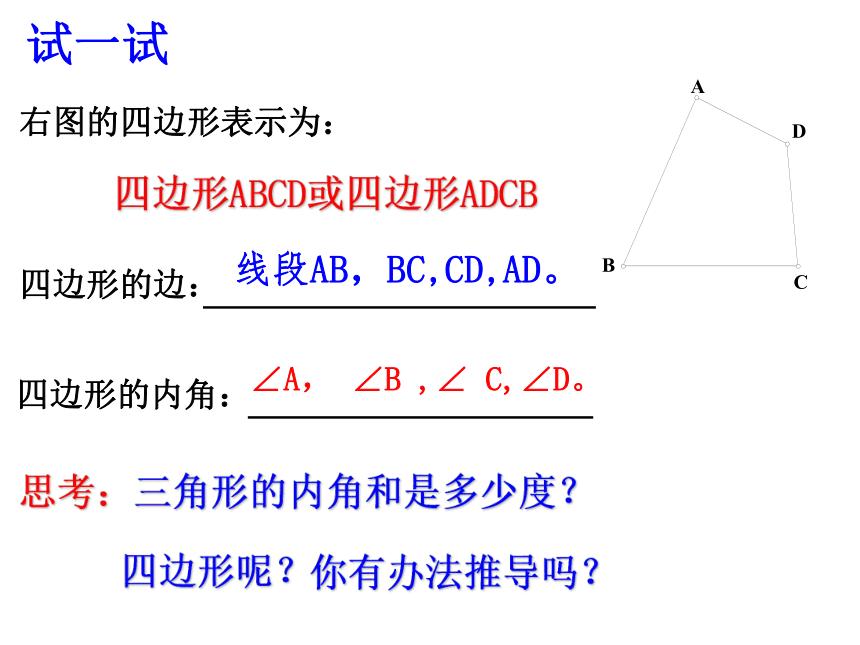
右图的四边形表示为：
四边形ABCD或四边形ADCB
四边形的边：
四边形的内角：
∠A， ∠B ,∠ C,∠D。
线段AB，BC,CD,AD。
试一试
思考：三角形的内角和是多少度？
四边形呢？
你有办法推导吗？
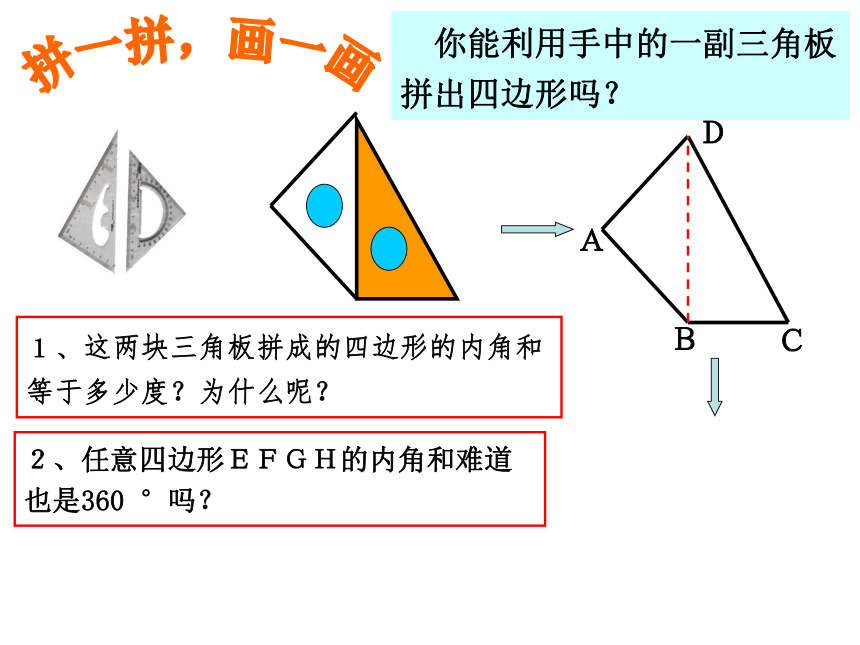
你能利用手中的一副三角板拼出四边形吗？
Ａ
Ｂ
Ｃ
Ｄ
１、这两块三角板拼成的四边形的内角和等于多少度？为什么呢？
２、任意四边形ＥＦＧＨ的内角和难道也是360 °吗？
探索：四边形的内角和等于360 °
动
脑
推
理
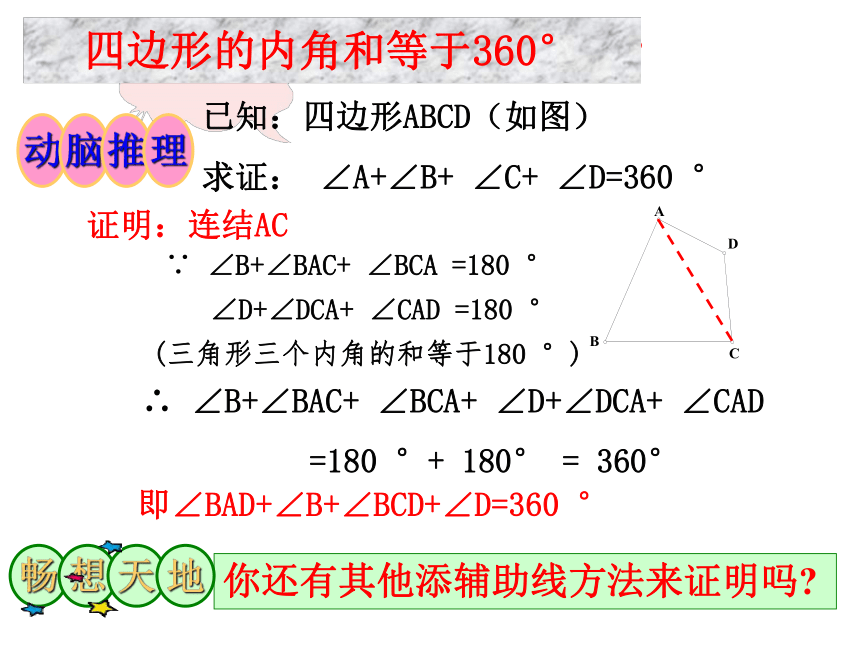
已知：四边形ABCD（如图）
求证： ∠A+∠B+ ∠C+ ∠D=360 °
证明：连结AC
∵ ∠B+∠BAC+ ∠BCA =180 °
∠D+∠DCA+ ∠CAD =180 °
(三角形三个内角的和等于180 °)
∴ ∠B+∠BAC+ ∠BCA+ ∠D+∠DCA+ ∠CAD
=180 °+ 180° = 360°
即∠BAD+∠B+∠BCD+∠D=360 °
你还有其他添辅助线方法来证明吗
畅
想
天
地
四边形的内角和等于360°
A
B
C
D
·
P
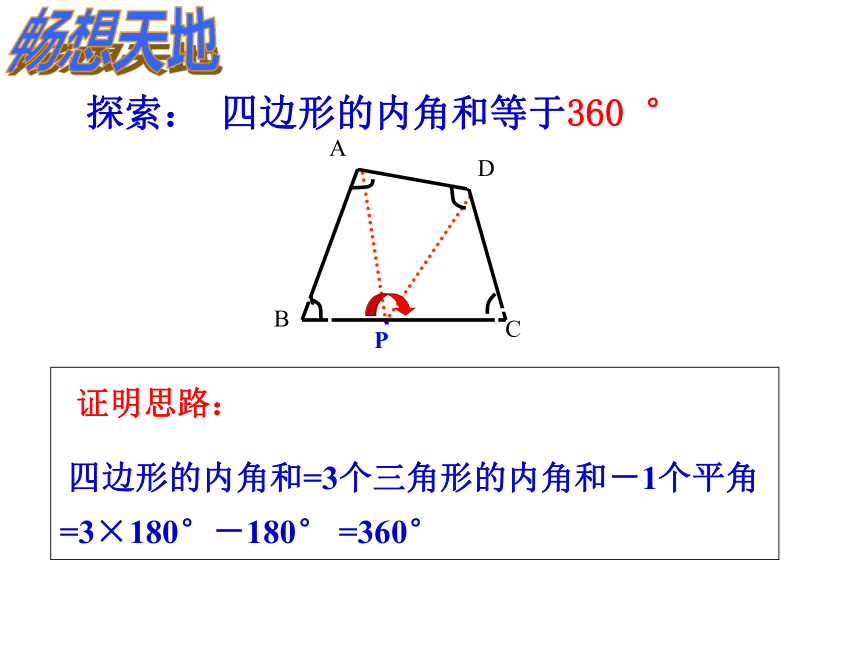
探索： 四边形的内角和等于360 °
证明思路：
四边形的内角和=3个三角形的内角和－1个平角 =3×180°－180° =360°
A
B
C
D
· O
证明思路：
四边形的内角和=4个三角形的内角和一1个周角
=4×180°－360° =360°
探索： 四边形的内角和等于360 °
探索： 四边形的内角和等于360 °
证明思路：
四边形的内角和=4个三角形的内角和一1个周角
=4×180°－360° =360°
A
B
C
D
A
B
C
D
∟
∟
A
B
C
D
A
B
C
D
探索： 四边形的内角和等于360 °
运用转化的思想方法可以让我们将复杂问题转化成我们熟悉的、已知的知识来求解.
例1、如图，四边形风筝的四个内角∠A、∠B、∠C、∠D的度数之比为1∶1∶0.6∶1，求它的四个内角的度数．
A
B
C
D
解：设∠A为x度，由题意可得：∠B，∠C，∠D分别为x，0.6x，x
∵∠A+∠B+∠C+∠D=3600
（四边形的内角和为3600）
∴x+x+0.6x+x=360
解得，x=100
∴∠A=∠B=∠D=1000，∠C=600
Ｃ
Ａ
Ｄ
Ｂ
1、如图，在四边形ＡＢＣＤ中，ＡＢ⊥ＢＣ， ∠Ａ＝ ∠Ｃ＝１００°，则∠Ｄ的度数为———°
７０
α
120
120
110
。
。
。
Ａ
Ｄ
Ｃ
Ｂ
2、如图，在四边形ＡＢＣＤ中， ∠Ｃ＝１１０°， ∠ＢＡＤ， ∠ＡＢＣ的外角都是１２０°，则∠ＡＤＣ的外角α的度数是————度。
５０
做一做
A
B
C
D
E
F
例2、（1）如图，在长方形ABCD中，BE平分∠ABC，交CD于点E，DF平分∠ADC，交AB于点F．问：DF是否平行于BE？请说明理由.
（2）若将上图的长方形ABCD改成如图∠A=∠C=900的四边形，其他条件不变。问：DF是否还平行于BE？请说明理由.
3
4
1
2
E
F
∠A=∠C
1．四边形最多有_____个直角？最多有_____个钝角？
4
3
练一练
2．已知四边形ABCD中,∠A＝90°,∠B:∠C:∠D =1:2:3，求∠B 的度数。
3、如图，已知四边形ABCD中，∠ A=∠B，∠D= ∠C，求证:AB//CD
D
A
B
C
练一练
4．如图，已知四边形ABCD中,∠A＝∠C，∠B=∠D。 （1）找出互相平行的边；
（2）若∠A与∠B的度数之比是1:2，求各内角的度数。
　清晨，小明沿着一个四边形广场周围的小路，从A点出发，按逆时针方向跑步．
（１）小明每从一条小路转到下一条小路时，身体转过的角是哪些角？
（２）他每跑完一圈，身体转过的角度之和是多少？
Ａ
Ｂ
Ｃ
Ｄ
1（
（
（
（
2
4
3
∠1、∠2、∠3、∠4
合作讨论
四边形的四个不同顶点外角和等于多少度？
已知：如图，∠５ ,∠ ６,∠７ ,∠８
是四边形的四个外角。
求：∠５＋∠６+ ∠７ +∠８ =？
５
D
A
B
C
６
７
８
１
２
３
４
解: ∵∠ 1+∠５ =∠2+ ∠６= ∠3+∠７ ＝∠ 4+∠８= 180°
∴ ∠ 1+∠５ +∠2+ ∠６+ ∠3+∠７+ ∠ 4+∠８
=4× 180°= 720°
即: (∠ 1+∠2 +∠ 3 + ∠4)+ (∠５ +∠ ６ + ∠ ７ +∠８) = 720°
∵ ∠１ +∠ ２ + ∠ ３ +∠４=360°(根据四边形的内角和是360°)
∴ ∠５+∠ ６+ ∠ ７ +∠８ = 720°－ 360°= 360°
推论: 四边形的外角和等于360°
1.已知四边形ABCD中，∠A＝80 °,∠B＝60°, ∠C=70°则∠D=_____.
3. 如图，在四边形ABCD中， ∠A=85 °，∠D＝110 °， ∠1的外角是71 °，则∠1＝____,
∠2＝____.
B
85 °
A
D
C
110 °
2
71 °
1
150 °
128 °
109°
56 °
2.已知四边形ABCD中，∠A与∠C互补，∠B＝80 °，则∠D＝ .
100°
4.已知四边形ABCD中， ∠A＝72 °, ∠B： ∠C ：∠ D =4：2：3 ,则其中最大的角为 .
填一填
三角形 四边形
图形
定义
顶点个数
边的条数
表示法
内角和
外角和
A
B
C
D
A
B
C
由不在同一条直线上的三条线段首尾顺次相接形成的图形叫三角形
3个
3条
可以表示为△ ABC、△ BCA、△ CAB等
180
360°
由不在同一直线的四条线段首尾顺次相接形成的图形叫做四边形。
4个
4条
可以表示为四边形ABCD、四边形BCDA、四边形CDAB、四边形DABC等。
360
360°
这节课你学到些哪些知识和数学方法？
本课学习的重要数学方法
三角形的概念 四边形的概念
四边形问题 三角形问题
类比
转化
（已知）
（未知）
（未知）
（已知）
小明还想把规格相同的四边形余料镶嵌成无缝隙的地板，同学们认为他能做到吗？请帮忙设计。
拓展探索
你们知道为什么能做到吗？
请你们用所学过的几何知识说明理由。
拓展探索
小明还想把规格相同的四边形余料镶嵌成无缝隙的地板，同学们认为他能做到吗？请帮忙设计。
作业
1、方法指导丛书 5.1（1）
2、课时导航 5.1（1）